递归小专题

递归定义

• 一个函数自己直接或间接调用自己

递归、函数调用的执行方式

通常，当在一个函数的运行期间调用另一个函数时，在运行被调用的函数之前，系统需完成3件事：（1）将所有的实在参数、返回地址等信息传递给被调用的函数保存；（2）为被调用的函数的局部变量分配储存区；（3）将控制转移到被调用函数的入口。 而从被调用函数返回调用函数之前，系统也应完成三件事：（1）保存被调用函数的计算结果；（2）释放被调函数的数据区；（3）依照被调用函数保存的返回地址将控制转移到调用函数。 当有多个函数构成嵌套调用时，按照“后调用先返回”的原则，上述函数之间的信息传递和控制转移必须通过“栈”来实现，即系统将整个程序运行时所需的数据空间安排在一个栈中，每当调用一个函数时，就为它在栈顶分派一个储存区，每当从一个函数退出时，就释放它的储存区，则当前正在运行的函数的数据区必在栈顶。

• A 函数调用 A 函数和 A 函数调用 B 函数在计算机看来时没有任何区别的，只不过用日常的思维方式理解比较怪异而已
• 图示：
  

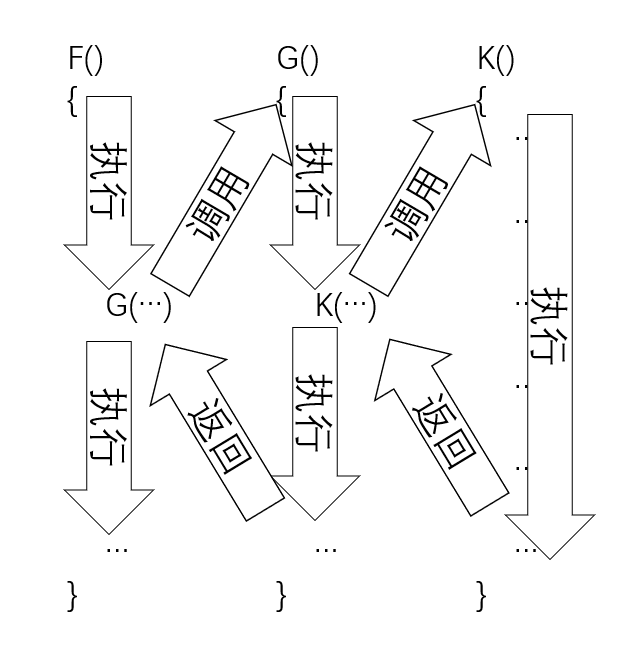
递归需满足的三个条件

1. 递归必须有一个明确的终止条件
2. 该函数所处理的数据规模必须在递减（要解决复杂度为 n 的问题，必须借助复杂度为 n - 1 的复杂度的问题的解决来解决，以此类推）
3. 这个转化必须时可解的

递归和循环的关系

1. 递归与循环的关系：所有能用循环解决的问题都能用递归解决，但是用递归能解决的问题用循环不一定能解决
2. 递归与循环的优缺点比较：
   • 递归：
     • 易于理解
     • 速度慢
     • 存储空间需求大
   • 循环
     • 不易理解
     • 速度快
     • 存储空间小

递归举例

• 1+2+3+4+···+100的值
• 求阶乘
• 汉诺塔
• 走迷宫

求阶乘

#include <stdio.h>
#include <stdlib.h>

int Factorial(int n);

int main()
{
    int n;
    printf("请输入要求阶乘的数字(要求数字大于零)：");
    scanf("%d",&n);
    if(n>=0){
        printf("所求阶乘结果为：%d",Factorial(n));
    }else{
        printf("所输入的数值小于0，程序结束");
        exit(-1);
    }
}

int Factorial(int n)
{
    if(n>1){
        return Factorial(n-1)*n;
    }else{
        return 1;
    }
}

汉诺塔

规则分析

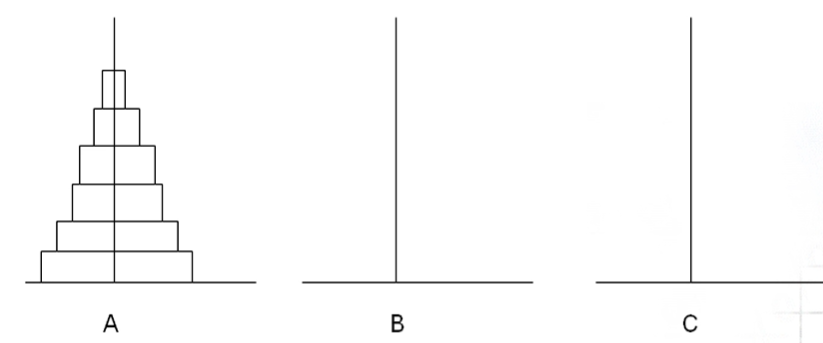
如何把 A 上的 n 个盘子借助 B 移动到 C 上，要求：

1. 一次只能移动一个盘子
2. 移动过程中大盘子永远不能放在小盘子上面

伪算法

• if ( n > 1)
• {
• 先把 A 柱子上的前 n-1 个盘子从 A 借助 C 移到 B
• 将 A 柱子上的第 n 个盘子直接移到 C
• 再将 B 柱子上的 n - 1 个盘子借助 A 移到 C
• }

汉诺塔实现

#include <stdio.h>

void hannuota(int n,char A,char B,char C);//A 代表盘子来源的柱子，B 为被借助的柱子，C 为目标柱子，ABC并不代表固定的某一个柱子

int main()
{
    char ch1='A';
    char ch2='B';
    char ch3='C';
    int n;

    printf("请输入要移动的盘子的个数：");
    scanf("%d",&n);

    hannuota(n,'A','B','C');
}

void hannuota(int n,char A,char B,char C)
{
    if(n==1){
        printf("将编号为%d的盘子直接从%c柱子移动到%c柱子\n",n,A,C);//A 代表盘子来源的柱子，B 为被借助的柱子，C 为目标柱子，ABC并不代表固定的某一个柱子
    }else{
        hannuota(n-1,A,C,B);//将 n - 1 个盘子从 A 借助 C 移动到 B
        printf("将编号为%d的盘子直接从%c柱子移动到%c柱子\n",n,A,C);//A 代表盘子来源的柱子，B 为被借助的柱子，C 为目标柱子，ABC并不代表固定的某一个柱子
        hannuota(n-1,B,A,C);//将 n - 1 个盘子从 B 借助 A 移动到 C
    }
}

递归的应用

• 树和森林就是以递归的方式定义的
• 树和图的很多短发都是以递归来实现的
• 很多数学公式就是以递归的方式定义的