2023-2-20 #40 只有回音在房间中旋转交织着暮光

——COP《回音》

最近停更的主要原因是打模拟赛比较 emo，做题也没做几道，就打算屯一起发出来。

没想到这么多人想看我博客，那我就整理整理发出来吧！

---

竟然有人怀疑我这些文章是不是闲话啊！！我原本的创作目的就是写写闲话！只是因为我文笔想象力都不太好，没有什么能说的，只能抱着点做过的题跟大家说说而已。

---

222 uoj#794. 【UR #24】比特之地

赛时就知道是 separator 了，可惜我并没有时间做！！(不过我做了也应该做不出来)

那场 A 写的线性做法竟然跑不了 1e6，uoj 什么垃圾评测机！！！

毕竟普通的 separator 只能做到根号大小，而一般平面图的 separator 太复杂了！我们不妨主动使用根号分治，构造一些更为简单的 separator。

若分治区域的树高不超过根号，一个直接的构造方法是：取出 dfs 序前一半每个深度 dfs 序最大的结点作为 separator，其合法性手玩一下就知道了，而且其将树划分成的较小的区域大小在 \(\frac n2\) 减根号左右。

否则一定有一层的宽度不超过根号，此时我们可以直接使用一般的构造方法取出两层 \(u,v\) 加上 \(u,v\) 之间一条路径构成 separator，但是比较难写！

一个更方便的方法是直接取最靠近深度中点，且宽度不超过根号的层作为 separator，其合法的原因是三次这样的划分同样可以得到上面描述的“工”字形！

225 AGC050F NAND Tree

当 \(n\) 是偶数时我们直接枚举第一次操作，我们仅考虑 \(n\) 为奇数的情况，此时操作数量为偶数。

我们将操作两两配对，如果两次操作互不影响则可以进行交换，贡献一定是偶数，因此两次操作选择的边一定有交点。

我们将两次操作放在一起描述，其包括的三个点 \(a,b,c\) 的邻边叠起来，并将新点点权赋为 \((a\operatorname{nand} b)\operatorname{nand} c\)。

我们打出 \((a\operatorname{nand} b)\operatorname{nand} c\) 的真值表，可以发现 \(a\ne c\) 时得到的就是 \(a\)，否则我们交换 \(a,c\) 得到双射，贡献为偶数，我们可以钦定其结果也是 \(a\)。

那么操作变成了：选择三个点 \(a,b,c\) 使得 \((a,b),(b,c)\) 有边，将三个点合并，新权值等于 \(a\) 权值，那么可以看成 \(a\) 吃掉 \(b\) 吃掉 \(c\)。

那么我们可以枚举最后剩下的结点，一个发现是若操作与 \(a\) 无关，我们可以反转这次操作得到一个双射，因此所有操作都是 \(a\) 吃掉两个点。

通过剥叶子可以得知与一个点同时被吃掉的点是固定的，即构造一个边的完美匹配。而边匹配之间的限制关系是树形的，只需做一个拓扑序计数就好了。

复杂度 \(O(n^3)\)，换根应该可以 \(O(n^2)\)。

226 CF1344E Train Tracks

一个很好的策略是：我们让每个点的出边空闲时指向重边，那么可以立即得到切换次数是 \(O(n\log n)\) 的，我们如果处理出所有要用切换的时刻问题就转换成：给定 \(O(n\log n)\) 个区间，每个区间都要找到一个唯一的操作时刻，这个通过给区间左端点排序，用堆维护贪心可以计算。

找到这些区间可以使用 dsu on tree，枚举轻子树的路径尾端点并找到其在当前子树所有路径时刻的前驱后继，分别考虑一下要不要操作就好了。

复杂度 \(O(n\log^2 n)\)。

227 CF1344F Piet's Palette

不难。

对颜色的刻画可以通过将 W,R,Y,B 映射成 \(0,1,2,3\)，mix 就代表异或。

RY，RB，YB 这些操作可以脑洞一下，分别变成交换高低两位，高位异或低位，低位异或高位。

因此我们可以列出 \(2m\) 个关于每个数高低位的异或方程组，bitset 高消即可，复杂度 \(O(\frac{n^2m}{w})\)。

228 几个经典的数论问题

别急，马上会写的！

229 AGC046F Forbidden Tournament / CF1338E JYPnation

手玩一下，找找性质。

• 缩点双，非最后一个点双都不能存在三元环，而事实上无三元环的强连通竞赛图都是单点，构造我们可以取出哈密顿回路不断取出中间一条边割成更小的回路。

我们枚举最后一个点双的大小，很容易计算其他点的贡献系数。

任选一个点 \(p\)，我们将连向 \(p\) 的点包括 \(p\) 作为集合 \(X\)，被 \(p\) 连向的点作为集合 \(Y\)，那么：

• \(X\) 形成链型，否则 \(X\) 中任意一个三元环都形成了给定子图。
• 对于 \(x\in X,y\in Y\)，若 \(y\rightarrow x\)，则对于所有 \(y\rightarrow y'\) 都有 \(y'\rightarrow x\)，否则有 \((p,x,y)\rightarrow y'\)。
• \(Y\) 形成链型，否则 \(Y\) 中任意点都不能到达 \(Y\) 中的一个三元环，而若不存在这个，这个三元环与点就形成了给定子图。
• 对于 \(x\in X,y\in Y\)，若 \(y\rightarrow x\)，则对于所有 \(x'\rightarrow x\) 都有 \(y\rightarrow x'\)，否则有点难证，我有点懒得写了，大概讨论一下链尾的连边就行了。

而如果满足以上条件，容易发现不存在给定子图，那么我们可以把 \(p=1\) 时的连边情况刻画成二维的一个阶梯型结构，两维分别代表 \(X,Y\) 集合，我们 \(O(n^2)\) dp 一下就好了。

复杂度 \(O(n^4)\)。

CF 那题是明显的弱化版，随便算算就行。

230 AGC061F Perfect Strings

把写 1/0 放在二维平面，那么相当于计数一个 torus 上经过 \((0,0)\) 的，只用下步、右步的简单环数量。

经过 \((0,0)\) 这个限制我们先不看，后面很容易处理。

我们观察简单环的形态，事实上是在上边界与左边界放置了若干出插头，下边界与右边界放置了若干入插头，按照顺序依次匹配插头连出若干组不交路径。

但是如果单纯这样刻画简单环，会让一个环拆分成若干个简单环，观察一下可以发现不会拆分当且仅当出插头与入插头数量互素。（假设上下插头数量 \(a\) 不少于左右插头数量 \(b\)，考察最靠右的上插头，其连向最靠上的右插头，然后其连向第 \(a-b+1\) 个下插头，对应到第 \(a-b+1\) 个上插头，那么一次可以跳 \(a-b\) 步，根据经典结论可知上面那个结论）

如果知道插头的位置我们当然可以直接 LGV 算不交路径方案数，可是我们不能暴力枚举每个插头是否存在。（注意 LGV 还有一个 \(-1\) 的逆序对数量系数，但是可以证明逆序对数量奇偶性一定是 \((nm-ij)\bmod 2\)）

为了保证上面那个性质，我们考虑用占位元 \(x,y\) 来表示左右插头与上下插头的数量，也就是如果占用这个左右/上下插头就会贡献 \(x/y\)，否则我们直接将这个左右/上下插头内部匹配，无贡献。

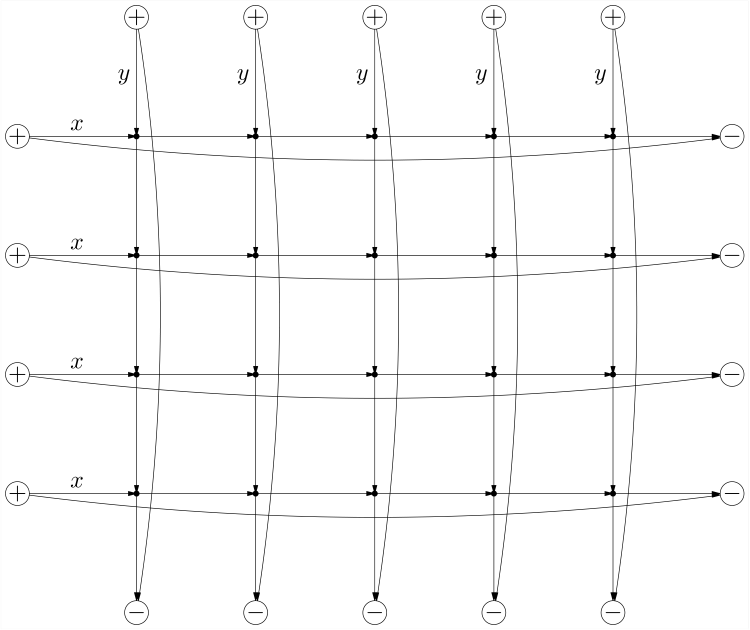
（注意这个图还是个 DAG）

那么就是这个图求 LGV 的多项式，对 \(x,y\) 两维插值就好了，复杂度是五次方的，你也可以对 \(y\) 插值，并利用 \(O(n^3)\) 的 \(\det(Ax+B)\) 做到 \(O(n^4)\)。

做法：
我们不妨先考虑 \(\det(Ix+B)\)，这是 P7776 【模板】特征多项式，方法是：
注意到相似矩阵特征多项式相同，我们尝试将矩阵消成上海森堡矩阵，具体地，我们使用基本行列变换消元，在进行一个操作后立即进行其对应的逆运算就能保证矩阵仍然相似。类似高斯消元，考虑某一列 \(i\)，若没有位置有值则不管，否则将这个值交换到 \((i+1,i)\)，并照常去消其他位置的值，可以发现不会污染已经做完的位置。
上海森堡矩阵行列式有 \(O(n^2)\) 递推方法，因为每个置换环一定是 \((i,i-1,\cdots,j,i+1)\)，因此可以直接递推出多项式。
做 \(\det(Ax+B)\) 是类似的，我们使用高斯消元将 \(A\) 消成 \(I\)，当 \((i,i)\) 一次项为 \(0\) 时，我们检查当前行是否有能换过来的值，若没有则将整行乘上 \(x\) 并重新拿之前的列消掉被污染的部分，注意这种操作只会出现 \(O(n)\) 次，否则一定无解。

上面经过 \((0,0)\) 的限制我们还没有考虑，事实上可以直接强制第 \(0\) 行没有跳过边或者强制第 \(0\) 列没有跳过边。

另一种方法是算经过每个点的方案数除以 \(nm\)，那么就是一个环造成环长的贡献，而我们若知道上下插头与左右插头的数量可以确定唯一的环长，这样就可以了。

231 AGC051C Flipper

hzr 秒了的结论题，可惜我不太会这种，(T_T)。

观察题目中的不变量，首先一列黑点奇偶性不变，一行模 \(3\) 为 \(0\) 与模 \(3\) 为 \(1\) 的数量奇偶性不变，\(1\) 与 \(2\) 这样的数量奇偶性也不变。

猜测这是充要的，具体我们可以从上到下从左到右递推证明。

假设 \(a,b,c\) 分别为模 \(3\) 为 \(0,1,2\) 的位置 \(1\) 数量奇偶性，那么行分为四类 \(000,001,010,100\)，你可以枚举每个行是否翻转，随便贪贪！！

232 AGC047F Rooks

别急，马上会写的！

233 ARC141F Well-defined Abbreviation

别急，马上会写的！

234 ARC147F Again ABC String

235 loj#3628. 「2021 集训队互测」树上的孤独

别急，马上会写的！

（贡献者：juju527）