2023-2-2 #32 就将心愿抛洒向天空 等待透明雪落下
——不鱼《愿望幽灵》
被锣鼓比赛 2C 薄杀了!只能说自己水平不行阿😭。
180 CF804F Fake bullions
弱智二合一。
这个 mod 就引导你用裴蜀,缩点双,设一个点双里 \(S\) 的 \(\gcd\) 为 \(d\),那么在 \(d\) 同余类中与所有点双内金条同余的人都可以拿到假金条。
于是很容易算出每个位置金条上界下界。
计数部分只需枚举金条最少的城市(金条相同需要钦定一个字典序),选择了的城市肯定都可以取最大值,其余都取最小值。
将城市分类,一定会被选上、一定不被选上和其他,组合数算一下就行了。
181 CF1764H Doremy's Paint 2
联考考了,我没改!im baiguai。
我们直接解决一个更难的问题:询问执行一个任意区间剩下的颜色数量。
我们不妨先把未被覆盖的点的贡献算掉,那么就是询问一个区间的区间交,经典的颜色段均摊。
如果一个位置被覆盖且产生贡献,其一定是某次操作的左端点,我们将这个颜色的贡献看成这次操作的贡献。
我们可以记录 \(L_i\) 表示 \(i\) 左端点上次被覆盖的时间,\(R_i\) 表示 \(i\) 这个操作影响完全消失的时间,如果求出其我们无非是数 \(L_i\leqslant ql\leqslant i\leqslant qr\leqslant R_i\),二维数点即可。
第一个在上面颜色段均摊的时候很容易求出,第二个事实上就是这个区间被完全覆盖的时间与 \(\max_{L_j=i}R_j\) 取 \(\max\) 的结果,从后往前计算就好了。
学习了一种很好写的写法!!发现上面的讨论其实非常冗余。
我们从后往前加区间,三个部分的计算可以使用同一个颜色段均摊完成,具体我们只需计算被覆盖过且不是有效区间左端点的点数。将 \([l+1,r]\) 先覆盖为 \(i\),并将 \([l,r]\) 内颜色最大值算出,将 \([l,l]\) 覆盖为最大值。我们询问就相当于询问 \(\leqslant t\) 的点数,一个树状数组就好啦。
复杂度 \(O(n\log n)\)。
182 u 群题
题意:单点修改,求区间 mex,强制在线。
一个很优秀的转化:对于某个数,找到其出现的上一次位置,那么这个开区间的所有子区间答案都不超过这个数。
因此问题变成了 \(O(n)\) 次在线的二维数点(单点修,矩形 min),树套树即可。由于限制是 2-side 的,外层可以使用树状数组,实现较为简便。
复杂度 \(O(n\log^2 n)\)。
183 ARC154F Dice Game
用 OGF 刻画从 \(x\) 种数字到 \(x+1\) 种数字的过程:
不同的过程独立,我们可以用分治 NTT 求出求出答案多项式 \(\frac{P(x)}{Q(x)}\)。
一个比较假的想法:
先令 \(F(x)=P(x)\cdot Q^{-1}(x)\),现在要根据答案多项式推出期望 \(k\) 次方值,使用 P7431 [THUPC2017] 小 L 的计算题 中的技巧:
\(ans_k=\sum_if_ii^k\\\sum_k\sum_if_ii^kx^k=\sum_if_i\sum_k(ix)^k=\sum_i\frac{f_i}{1-ix}\)
分治通分即可,复杂度 \(O(n\log^2 n)\)。
假的原因是 \(F(x)\) 是无限多项式,不能直接截断。
正确的做法是把上面的过程看成复合 \(e^x\),但 \(e^x\) 有常数项,我们应该上下分别复合 \(e^x\),复合 \(x-1\),截断,再求逆。
很神秘阿,好像有人做法是直接复合 \(e^x\) 然后截断求逆的,不知道为啥对!如果有老哥会能不能教教我!!
复合 \(e^x\) 与上面的推导过程是一致的。
这个东西好像比较深刻,我并不是很会!事实上使用矩母函数可以得到一种比较机械的做法?
具体我们直接应用几何分布,将这些几何分布的矩母函数乘起来,再复合就好了。(过程是一致的,只是思路更为自然)
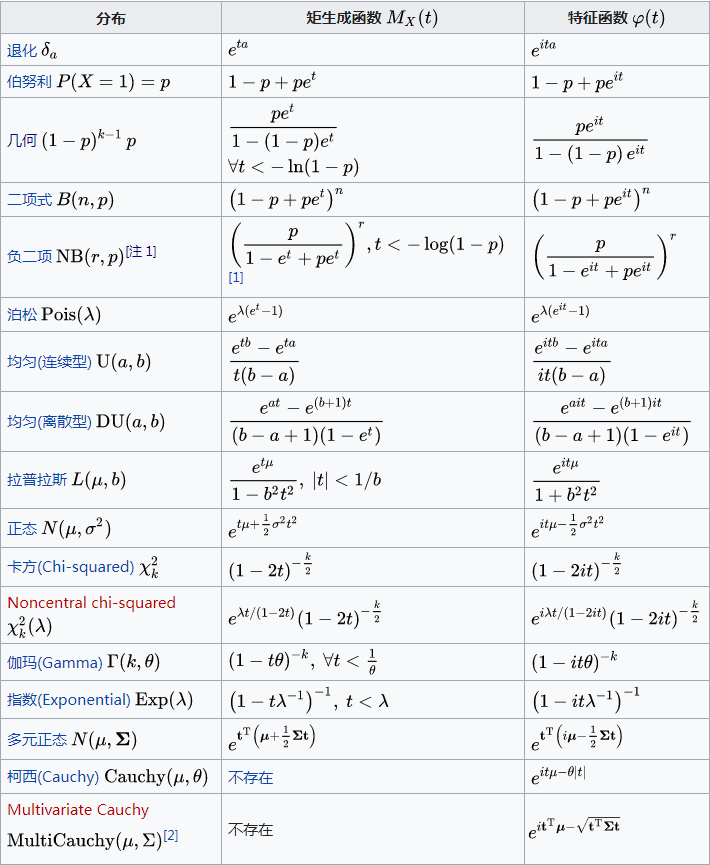


 浙公网安备 33010602011771号
浙公网安备 33010602011771号