二分图网络流做题记录
01 P4589 [TJOI2018]智力竞赛
二分一手答案，我们发现就是要覆盖指定的链，跑一边传递闭包就是 DAG 点覆盖了。
02 P3973 [TJOI2015]线性代数
先转化一手式子：
\[D=\sum_{i=1}^n a_i\times(\sum_{j=1}^n a_j\times b_{j,i}-c_i)=\sum_{i=1}^n\sum_{j=1}^n a_ia_jb_{i,j}-\sum_{i=1}^n a_ic_i
\]
考虑每个位置选 \(0\) 还是选 \(1\) 明示最大闭合子图，于是我们可以考虑这样的模型：
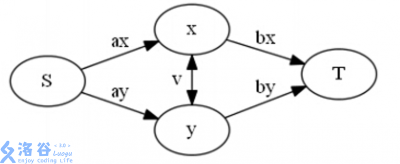
（洛谷题解的图）
考虑每一种割的形态，解方程可得：
\[ax=b_{x,x}+\frac{1}{2}(b_{x,y}+b_{y,x}),ay=b_{y,y}+\frac{1}{2}(b_{x,y}+b_{y,x})\\bx=c_x,by=c_y\\v=\frac{1}{2}(b_x+b_y)
\]
我们发现扩展到多个点的情况只需要把 \(ax,ay\) 后面的东西变成对于所有 \(y\) 的和就好了。
03 CF863F Almost Permutation
简单题，每个位置对应的所有值都建一个点，限制就给位置以及对应的值连个边，让流量做到最大流即可，而费用采用经典方法，连 \(n\) 条边，第 \(i\) 条费用为 \(2i-1\) 即可。
04 P4249 [WC2007]剪刀石头布/CF1264E Beautiful League
考虑简单容斥一手，我们要算不是三元环的数量最小值。
观察可得不是三元环等价于一个点出度为二，一个点入度为二，一个点出度为一入度为一，那么实际上这等价于存在一个点入度为二，也就是说答案是 \(\sum_{i=1}^n {indeg_i\choose 2}\)。
这个东西是单增的，于是直接套路建图一波带走。
05 CF802C Heidi and Library (hard)/CF132E Bits of merry old England
考虑保持一个书不好表示，可以看作卖掉这个书再买进来。
可以考虑每个点拆成两个点 \(v,v'\)，然后这样建图：（设 \(pre_i\) 为 \(i\) 这个颜色上一次出现的位置）
\[S\rightarrow v(1,c_{a_i})\\v\rightarrow v'(1,0)\\v'\rightarrow T(1,0)\\i\rightarrow i+1(k-1,0)\\i-1\rightarrow pre_i'(1,-c_{a_i})
\]
AC 记录（这个输出方案太恶心了/ll）
浙公网安备 33010602011771号