Examples

组合计数瞎做

01 CF1392H ZS Shuffles Cards

首先有一个比较有趣的转化：期望抽牌轮数等于每次抽到 joker 时抽牌数量乘期望抽到 joker 次数。

可以发现前面的东西是常数，由于每张牌排在所有 joker 前面的概率是独立的，为 \(\frac{1}{m+1}\)，所以一个期望抽牌序列长度为 \(\frac{n}{m+1}+1\)。（后面还有一张 joker）

考虑设 \(f_x\) 表示还有 \(x\) 张牌没有抽到时期望抽 joker 次数，那么我们讨论下一张牌是否是 joker：（注意洗牌不会清空你抽到过的牌集合）

\[f_x=\frac{m}{m+x}(f_x+1)+\frac{x}{m+x}f_{i-1} \]

由于 \(f_1=m+1\)，所以我们可以通过数学归纳法得到 \(f_n=1+\sum_{i=1}^n\frac{m}{i}\)。

然后就没了，时间复杂度：\(O(n)\)。

02 P2767 树的数量

显然可以设计出来一个 \(O(n^3)\) 的 dp：

\(f_{i,j}\) 表示 \(i\) 个节点，根节点 \(j\) 叉的方案数，转移可以前缀和一手转移一下，比较 naive。

好像有非常高明的做法，暂时鸽了：Fuss-Catalan 数、(m-1)-Dyck 路与 m 叉树，广义二项级数 & 广义指数级数学习笔记

大概就是经典结论，若生成函数 \(F_k(z)=zF_k^k(z)+1\)，那么：

\[[z^n]F^m_k(z)=\frac{m{kn+m\choose n}}{kn+m} \]

带入这道题就是

\[\frac{nm+1\choose n}{nm+1}=\frac{nm\choose n-1}{n} \]

lucas 定理即可，时间复杂度 \(O(mod)\)，好像可以卷积？

03 P3330 [ZJOI2011]看电影

正睿金华讲过的题，好像有点不太记得了。

首先特判 \(n>k\)。

dp 设计应该比较简单 \(f_{i,j,k}\) 表示到达第 \(i\) 位置，有 \(j\) 个人在等待，有 \(k\) 个人落座的概率，然后就枚举当前开始的人数量转移就好了，复杂度是 \(O(Tn^3k)\)，过不去。

我们发现实际上枚举多的人数可以类似前缀和优化，就可以做到 \(O(Tn^2k)\) 了，勉强能过。

但是实际上有高明的组合意义做法：

我们令序列后面添加一个新的座位，再将它变为一个环，那么我们每个人就都一定能落座，题意转化为没有人坐在最后一个座位的方案数。

我们发现成环之后每个点都是相同的，于是我们就可以钦定一个位置不选，那么概率为：

\[\frac{\frac{(k+1)^n}{k+1}\times(k+1-n)}{k^n} \]

左边是圆排列，右边就是钦定那个不选的位置在哪里。

时间复杂度 \(O(\log mod)\)，好像要高精度，直接用 python 省事了。

Bonus Problem：恰好 \(m\) 个人没有座位坐。

容斥一手，转化为至多 \(m\) 个人没有座位。

类似上面的问题，我们能在后面添 \(m+1\) 个座位再连成环，那么我们就要求最后一个位置没有人坐的概率。

如果我们套用上面的式子，那么可能会在第一次选的时候选中新加且不是最后一个的位置（称这种位置为坏位置）：

\[\frac{(k+m+1)^{n-1}(k+m+1-n)}{k^n} \]

设 \(f_{n,m,k}\) 表示 \(n\) 个人 \(k\) 个座位有至多 \(m\) 个人没有座位坐的方案数，考虑在上面的式子基础上计算不合法的方案：

\[f_{n,m,k}=(k+m+1)^{n-1}(k+m+1-n)-\sum_{i=1}^m{n\choose i}(m+1)^{i-1}(m+1-i)f_{n-i,m,k} \]

我们发现后面的 \(m,k\) 是不变的，于是我们可以递推，时间复杂度 \(O(nm)\)。

04 CF838D Airplane Arrangements

竟然秒了/jk

考虑直接在上一道题的基础上乘 \(2^m\) 即可。

05 CF1528F AmShZ Farm

多项式内鬼。/fn

暂鸽。

06 [数据删除]

07 P5591 小猪佩奇学数学

首先考虑 \(k=1\) 的情况：

\[\sum_{i=0}^n{n\choose i}p^ii=n\sum_{i=1}^n{n-1\choose i-1}p^i=np(p+1)^{n-1} \]

而这个 \(\lfloor\frac{i}{k}\rfloor\) 不太好处理，我们考虑一个比较显然但难以发现的结论：

\[\lfloor\frac{i}{k}\rfloor=\sum_{j=1}^i[k\mid j] \]

考虑单位根反演：

\[\sum_{i=0}^n{n\choose i}p^i(\sum_{j=0}^i[k\mid j]-1)\\=\sum_{i=0}^n{n\choose i}p^i\sum_{j=0}^i\frac{1}{k}\sum_{t=0}^{k-1}\omega_k^{jt}-(p+1)^n\\=\frac{1}{k}\sum_{t=0}^{k-1}\sum_{i=0}^n{n\choose i}p^i\sum_{j=0}^i\omega_k^{jt}-(p+1)^n\\=\frac{1}{k}\sum_{t=0}^{k-1}\sum_{i=0}^n{n\choose i}p^i\frac{\omega_k^{(i+1)t}-1}{\omega_k^t-1}-(p+1)^n\\=\frac{1}{k}\sum_{t=0}^{k-1}\frac{\omega_k^t\sum_{i=0}^n{n\choose i}p^i(\omega_k^t)^i-\sum_{i=0}^n{n\choose i}p^i}{\omega_k^t-1}-(p+1)^n\\=\frac{1}{k}\sum_{t=0}^{k-1}\frac{\omega_k^t(p\omega_k^t+1)^n-(p+1)^n}{\omega_k^t-1} \]

注意到 \(t=0\) 的时候除数为 \(0\)，可以分开算一手，答案是

\[\sum_{i=0}^n{n\choose i}p^i(i+1)=np(p+1)^{n-1}+(p+1)^n \]

直接算即可，时间复杂度 \(O(k\log n)\)。

08 P3200 [HNOI2009]有趣的数列

猜答案是卡特兰数。

考虑偶数位置一定大于它前面所有位置，我们将 \(1\cdots n\) 放入数列，则每一个时刻放到偶数位置的数数量不能超过奇数位置，于是卡特兰数即可。

由于模数不是质数，所以计算比较复杂，需要把每个数分解称其质因子乘积再计算。

09 CF1204E Natasha, Sasha and the Prefix Sums

首先考虑枚举这个最大值 \(k\)，但是恰好为最大值不好做，考虑转化为大于等于最大值 \(k\)。

转化为经典格路模型，那么可以看作这条路径与 \(y=k\) 相交。

如果起点和终点不在 \(y=k\) 一侧，那么一定相交，答案就是路径方案数。如果在同一侧，我们考虑这条路径与 \(y=k\) 的交点，我们翻折这个交点之前的所有路径，容易发现这与从翻折后的起点到终点的路径一一对应，于是组合数计算即可。

时间复杂度 \(O(n+m)\)。

10 AT2705 [AGC019F] Yes or No

格路计数大魔王！！！

暂鸽。

11 AT2070 [ARC061D] 3人でカードゲーム / Card Game for Three

竟然自己做出来了。

考虑刻画成一个三维格路模型，我们从 \((0,0,0)\) 出发，到达 \((n,a,b)\)（其中 \(0\leqslant a\leqslant m,0\leqslant b\leqslant k\)）。

容易发现一个终点 \((n,a,b)\) 对答案的贡献为 \(3^{a+b}\)，那么可以列出式子：（注意最后一次操作一定是 \(A\)）

\[\sum_{a=0}^m\sum_{b=0}^k3^{a+b}{n-1+(m-a)+(k-b)\choose n-1,m-a,k-b}\\=\sum_{T=0}^{m+k}3^{m+k-T}{n-1+T\choose n-1}\sum_{p=T-k}^{m}{T\choose p} \]

后面的东西是组合数前缀和，不好直接计算，考虑递推，设 \(f(x)=\sum_{p=x-k}^m{x\choose p}\)。

套路裂项：

\[f(x)=\sum_{p=x-k}^m{x-1\choose p-1}+{x-1\choose p}\\=\sum_{p=x-k-1}^{m-1}{x-1\choose p}+f(x-1)-{x-1\choose x-1-k}\\=2f(x-1)-{x-1\choose x-1-k}-{x-1\choose m} \]

递推即可，时间复杂度 \(O(n+m+k)\)。

12 联考题-二龙戏珠

题意是给定一条直线 \(y=ax+b\)，求不越过直线的 \((n,an+b)\) 自由路数量。（下文设 \(m=an+b\)）

结论很简单，\({n+m\choose n}-A{n+m\choose n-1}\)。

首先考虑 \(a=1\) 的情况，即给定的直线为一条平行于 \(y=x\) 的直线的情况。

这是经典的折线法问题，我们考虑翻折不合法的路径与 \(y=x+b\) 的最后一个交点，将不合法的路径与到达 \((n-1,m+1)\) 的路径一一对应。

然后是 \(a>1\) 的情况，我们考虑举第一个越过直线的整点 \((x,ax+b+1)\)，由于翻折这个位置之后的路径之后路径可能不再与坐标轴平行，所以我们不用翻折，直接列式子计算方案数：

\[\sum_{x=0}^{n-1}{(n-x)+(m-ax-b-1)\choose n-x}=\sum_{i=0}^n\frac{m-(ax+b)}{n-x}{(n-x)+(m-ax-b-1)\choose n-x-1}\\=a\sum_{i=0}^{n-1}{(n-x)+(m-ax-b-1)\choose n-x-1} \]

我们发现这个的组合意义实际上就是枚举到达 \((n-1,m+1)\) 的路径。（也就是说一条不合法的路径对应 \(a\) 条到达 \((n-1,m+1)\) 的路径）

然后直接组合数爆算就可以了，时间复杂度 \(O(n+m)\)。

13 P3266 [JLOI2015]骗我呢

首先发现题目中值域为 \([0,m]\)，这一点比较特别，考虑从这里下手。

由于一行是递增的，所以我们每一行最多会有一个间隔使得两边的数差为 \(2\)，换句话说，一行整个值域的数只会有一个数不出现。

考虑一种朴素的 dp，设 \(f_{i,j}\) 表示第 \(i\) 行 \(j\) 没有出现的方案数。

手动模拟一下过程可以得到转移方程，然后前缀和优化一波：

\[f_{i,j}=\sum_{k=0}^{j+1}f_{i-1,k}\\g_{i,j}=g_{i,j-1}+g_{i-1,j+1} \]

边界应该是 \(f_{1,0}=f_{1,1}=\cdots=f_{1,m}=1\)。

考虑这个转移方程的组合意义：从起点出发，每次可以向右或向左下走一步，不能越过网格边界，到达 \((n,m)\) 的方案数。

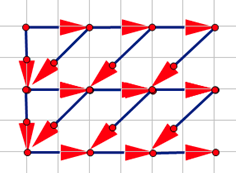
旋转：

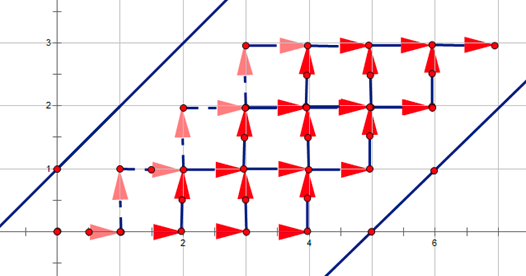
（蒯了几张洛谷题解的图）

那么就转化成了一个经典格路计数问题：求所有不经过 \(y=x+1,y=x-(m+2)\) 这两条直线的 \((n,n+m+1)\) 自由路数量。

考虑所有不合法的情况，其穿过这两条直线 \(A,B\) 的情况一定会变成一个序列 \(ABAABBBAA\cdots\)。

我们把连续的 \(A,B\) 缩在一起，那么我们可以对于 \(A,B\) 间隔的后缀（注意有两种）进行容斥。（前缀也行，不过后缀方便一些）

具体就可以发现每次容斥就将折线对着某一条直线进行翻折，这样这个问题就可以在 \(O(n+m)\) 内解决了，具体实现非常简单。

注意由于网格图经过了旋转，我们作对称的直线应该是 \(y=x-1,y=x+(m+2)\)。

14 AGC018E Sightseeing Plan

暂鸽。

15 P6689 序列

暂鸽。

16 CF997C Sky Full of Stars

这么弱智的转化都没有想到/ll。（除了第一步都想出来了）

首先一个~~很显然~~的转化就是容斥成没有一行一列是颜色相同的。

然后就是套路了，\(f_{i,j}\) 表示恰好 \(i\) 行 \(j\) 列颜色相同（\(f_{0,0}\) 即为所求），\(g_{i,j}\) 表示至少 \(i\) 行 \(j\) 列颜色相同，这样就可以进行二项式反演了。（下文称颜色相同的行/列为特殊行/列）

\[f_{0,0}=\sum_{i=0}^n\sum_{j=0}^n(-1)^{i+j}{n\choose i}{n\choose j}g_{i,j} \]

观察 \(n\leqslant 10^6\)，所以我们需要把 \(g\) 表示成一个简洁的形式便于化简。

当 \(i>0\) 且 \(j>0\) 的时候可以发现所有特殊行列颜色相同，否则特殊行/列相互不影响，于是列出式子：

\[g_{i,j}=\begin{cases}3^{(n-i)(n-j)+1}&i>0,j>0\\3^{n^2-(n-1)i-(n-1)j}&\text{otherwise}\end{cases} \]

我们发现 \(i=0\) 或 \(j=0\) 的式子都可以快速计算，考虑计算剩余的部分：

\[3^{n^2+1}\sum_{i=1}^n(-1)^{i}{n\choose i}3^{-ni}\sum_{j=1}^n(-1)^{j}{n\choose j}3^{(i-n)j} \]

后面的东西一脸二项式定理，可以直接写成 \((1-3^{i-n})^n-1\)，那么总共的复杂度就是 \(O(n\log mod)\) 了。

17 P5400 [CTS2019]随机立方体

暂鸽。

18 AT4119 [ARC096C] Everything on It

考虑对至少出现两次进行容斥，即我们枚举有 \(k\) 个数出现不足两次。

那么对于剩下的数我们先任意放入任意个子集中，然后再将我们钦定的数字选择一个子集或不加入，尝试列出式子。

上面是错误思路，我们发现这个顺序会让后面的贡献与子集大小有关，非常不好搞，于是考虑先将钦定的数字分成若干个集合，并新建一个集合作为垃圾堆放置没有出现的数字。

剩下的 \(n-k\) 个数字可以新建至多 \(2^{n-k}\) 种集合，同时也可以将集合与之前的集合合并，这样就可以列出式子了：

\[\sum_{k=0}^n (-1)^k{n\choose k}\sum_{i=0}^k \begin{Bmatrix}k+1\\i+1\end{Bmatrix}2^{2^{n-k}}(2^{n-k})^j \]

暴力计算即可，时间复杂度 \(O(n^2)\)。

19 P4827 [国家集训队] Crash 的文明世界 / SP7363 TREESUM - Tree Sum

\(k\) 次方考虑第二类斯特林数展开。

\[S(x)=\sum_{i=1}^n\sum_{j=1}^k\begin{Bmatrix}k\\j\end{Bmatrix}{dis(x,i)\choose j}j!\\=\sum_{j=1}^k\begin{Bmatrix}k\\j\end{Bmatrix}j!\sum_{i=1}^n{dis(x,i)\choose j} \]

考虑在外面枚举 \(k\)，然后通过 \(O(n)\) 来统计所有的位置后面那个东西的和。

这个东西一脸换根 dp 的样子，考虑求出每个点子树的答案，设 \(f_{x,k}=\sum_{y\in tree(x)}{dis(x,y)\choose k}\)，我们暴力展开组合数可以得到 \(f_{x,k}=(\sum_{y\in son(x)}f_{y,k}+f_{y,k-1})+[k=0]\)。

那么同样地可以换根得到每个点全局的答案，时间复杂度 \(O(nk)\)。

20 CF961G Partitions

我们考虑集合权值前面乘的 \(|S|\) 的组合意义为给每一个集合内的元素贡献后面的权值，因此我们可以枚举一个元素对自己和别的元素的贡献：（后面的意义为强制取出一个数在分组之后再放入 \(i\) 所在的组）

\[\sum_{i=1}^nw_i(\begin{Bmatrix}n\\k\end{Bmatrix}+(n-1)\begin{Bmatrix}n-1\\k\end{Bmatrix}) \]

后面的东西可以直接 \(O(n)\) 计算斯特林数。

21 P6162 [Cnoi2020]四角链

我们考虑一个 naive 的 dp，设 \(f_{i,j}\) 表示长度为 \(i-1\)，一共用了 \(j\) 个数的方案数。

\[f_{i,j}=f_{i-1,j}+(i-j)f_{i-1,j-1} \]

这个东西可以归纳证明 \(f_{n,m}=\begin{Bmatrix}n\\n-m\end{Bmatrix}\)。

22 ABC154F Many Many Paths

放松训练。

差分转化一手，那么就是求：

\[\sum_{i=1}^r\sum_{j=1}^c{i+j\choose i} \]

下指标求和一手：

\[\sum_{i=1}^r{i+c+1\choose i+1} \]

然后就没了/qd。

23 P4229 某位歌姬的故事

可以发现若一个区间满足了一个最大值更小的条件，那么整个区间都不能对最大值更大的条件造成贡献，，因此我们将限制按照最大值排序，每次对于一个固定的最大值进行处理。

处理最大值为 \(m\) 的位置可以考虑预处理一下每个位置能达到的最大值，把这些能达到最大值的位置取出来，大力 dp 一手，设 \(f_{i,j}\) 表示 \(i\) 这个位置之前达到最大值的位置为 \(j\) 的方案数，直接转移即可。

时间复杂度 \(O(Tn^2)\)。

24 CF294C Shaass and Lights

放松训练。

容易发现任意长度为 \(x\) 的熄灭段的方案数都是 \(2^{x-1}\)，然后若干段合并组合数即可，时间复杂度 \(O(n)\)。

25 P6667 [清华集训2016] 如何优雅地求和

套路地将组合数和多项式转化为下降幂和多项式，我们记这个多项式的下降幂形式为：

\[\sum_{i=0}^m f_ix^{\underline i} \]

然后就是推式子部分了：

\[\sum_{i=0}^m {n\choose i}x^i(1-x)^{n-i}\sum_{j=0}^m f_ji^{\underline j}\\=\sum_{j=0}^m f_jj!\sum_{i=0}^m{n\choose i}{i\choose j}x^i(1-x)^{n-i}\\=\sum_{j=0}^m f_jj!x^j{n\choose j}\sum_{i=j}^m{n-j\choose i-j}x^i(1-x)^{n-i-j}\\=\sum_{j=0}^m f_jj!x^j{n\choose j}(x+1-x)^{n-j}\\=\sum_{j=0}^m f_jx^j n^{\underline j} \]

考虑怎么转下降幂，我们列出式子：

\[\sum_{i=0}^m\frac{f(i)x^i}{i!}=\sum_{i=0}^m\frac{x^i}{i!}\sum_{j=0}^m f_ji^{\underline j}=\sum_{j=0}^m f_j x^j\sum_{i=0}^m\frac{x^{i-j}i^{\underline j}}{i!}=\sum_{j=0}^m f_jx^j\sum_{i=0}^m\frac{x^{i-j}}{(i-j)!} \]

我们发现 \(f\) 可以通过 \(\sum_{i=0}^m\frac{f(i)x^i}{i!}\) 卷上 \(e^{-m}\) 得到，时间复杂度 \(O(m\log m)\)，好像 EI 有 \(O(n)\) 做法，不会。

26 ARC102E Stop. Otherwise...

不会 sb 题，自闭了。

我们考虑对于某一个 \(x\)，我们可以将骰子的点数 \(t\) 分成三类：\(1\leqslant x-t\leqslant k\)（选了一个对应的点数就不能选，可以选若干），\(x-t=t\)（只能选不超过一个），\(\text{otherwise}\)（任意选）。

而容易发现这三类的贡献互不影响，我们考虑 dp 出 \(f_{i,j}\) 表示 \(i\) 个一类，一共用了 \(j\) 个的方案数，\(g_{i,j}\) 表示 \(i\) 个三类，一共用了 \(j\) 个的方案数。输出答案的时候就枚举用不用第二个，然后将另外两个卷起来就好了。

考虑怎么 dp：（第一个式子乘二的原因是两个数都可以用）

\[f_{i,j}=f_{i-1,j}+2\sum_{k=1}^jf_{i-1,j-k}\\g_{i,j}=g_{i-1,j}+\sum_{k=1}^j g_{i-1,j-k} \]

容易发现可以前缀和优化，时间复杂度 \(O(nk)\)。

27 P6478 [NOI Online #2 提高组] 游戏

老套路题。

恰好为 \(k\) 考虑二项式反演，设 \(f_k\) 为至少有 \(k\) 个胜负的情况数，发现这个东西可以树上背包一手，复杂度 \(O(n^2)\)。

28 CF1528E Mashtali and Hagh Trees

观察第三个性质，我们发现实际上等价于存在一个根，从其延伸出去的链都是单向的。

也就是说，满足要求的有向树都是内向树和外向树拼起来的。（或者单个内向/外向树）

我们先考虑对外向树计数，容易发现内向树与其等价，而拼起来的树可以暴力对外向树进行卷积。

设 \(f_x\) 为最长有向链长度为 \(x\) 的根度数不超过 \(2\) 的外向树数量，容易得到 \(f\) 的转移方程：（因为点无标号，所以两个 \(x-1\) 的时候要去重）

\[f_x=f_{x-1}+f_{x-1}\times\sum_{i=0}^{x-2}f_i+\frac{f_{x-1}\times(f_{x-1}+1)}{2} \]

最后长度为 \(x\) 的链的答案就是：

\[f_x+\frac{f_{x-1}\times(f_{x-1}+1)}{2}\sum_{i=0}^{x-2}f_i+f_{x-1}\frac{(\sum_{i=0}^{x-2}f_i)(\sum_{i=0}^{x-2}f_i+1)}{2}+\frac{f_{x-1}\times(f_{x-1}+1)\times(f_{x-1}+2)}{6} \]

注意长度为 \(n\) 的链会在内向和外向树中算重，所以内外向树的答案就是上面的乘二减一。

卷一卷就可以了，时间复杂度 \(O(n)\)。（下面右边要减一手是因为要钦定第二棵树需要有两个儿子避免算重）

\[\sum_{i=0}^{n-2}(f_i-1)(f_{n-i-1}-f_{n-i-2}) \]

29 P5481 [BJOI2015] 糖果

首先容易发现行之间没有影响，也就是说我们只需要求出值域为 \(k\) 长度为 \(m\) 的不降序列数量就可以了。

这个东西也很简单，考虑这个东西等价于 \(m\) 个球放入 \(k\) 个盒子可空的方案数，转化一手就是 \(m+k\) 个球放入 \(k\) 个盒子非空的方案数，即 \({m+k-1\choose k-1}\)，答案就是 \({m+k-1\choose k-1}^{\underline n}\)。

计算这个组合数比较麻烦，首先将其表示为 \({m+k-1\choose m}\)，我们可以将 \(m!\) 用素数表示出来，然后用每一个表示出的素数去筛 \(k,k+1,\cdots,k+m-1\)，由于这些数是连续的，所以我们可以类似调和计数地筛，复杂度明显是 \(O(m\log m+n)\) 的。

30 CF888F Connecting Vertices

看到 \(n=500\)，考虑三次方算法，断环为链然后区间 dp。

由于边不能相交，所以i我们发现考虑了左/右端点的一个连边，那么剩下的两个部分是不想管的，我们只需要随便讨论一下就可以了。

实际上还是有一点点问题，我们要在状态里对左右端点是否连边进行规定即可，时间复杂度 \(O(n^3)\)。

31 P5598 【XR-4】混乱度

已经快一天没有计数了，计数♥♥♥

首先求混乱度是一个经典问题：

\[f(l,r)=\frac{(\sum_{i=l}^r a_i)!}{\sum_{i=l}^r a_i!} \]

很容易通过移动右端点维护左端点答案的方法做到 \(O(n^2\log_p m)\)。（\(m\) 为值域）

模数比较小，考虑从此入手。

根据 Lucas 定理，我们可以发现从一个左端点开始我们只需要移动 \(O(1)\) 步就可以使得答案模 \(p\) 余 \(0\)，那么我们维护 \(O(1)\) 项的答案即可，时间复杂度 \(O(n)\)。（思路是错的）

看题解后：实际上也没有那么神仙。。。。

实际上上面的做法只能应用于数据随机的情况，\(a=0\) 的情况直接卡掉。

考虑优化一手，首先把所有 \(0\) 缩在一起，这样的复杂度是多少呢？我们考虑 Kummer 定理，\(n+m\) 在 \(p\) 进制下若进位则说明 \({n+m\choose n}\bmod p=0\)，而缩掉 \(0\) 之后至少有一个位置会加一，于是复杂度是 \(O(np\log_p^2 m)\)（注意使用 Lucas 定理计算组合数带个 \(\log\)）

实际上我们不需要每次使用 Lucas 定理计算，我们可以直接递推。枚举每个 \(p\) 的幂次，预处理组合数，每次向右移动的时候就让每个幂次都乘个组合数，这样优化一手复杂度就是 \(O(np\log_p m)\) 了，可以通过。

实际上上面的过程等价于使用 Kummer 定理进行数位 dp。

32 AGC028D Chords

好，再次不会做。

考虑一个连通块在圆上实际上对应着一段区间（反之不然）。又因为 \(n\) 是 \(300\)，考虑区间 dp。

我们只需要计算出每个连通块的出现次数，加起来即可。

设 \(f_{l,r}\) 表示仅考虑 \([l,r]\) 这个区间内的连边，使得 \(l,r\) 联通的方案数，\(g_{l,r}\) 表示 \([l,r]\) 任意连边的方案数。

设 \([l,r]\) 内有 \(k\) 个点可以连边，容易发现 \(k\) 为奇数则 \(g_{l,r}=0\)，否则 \(g_{l,r}=k!!\)。

直接算不好搞，考虑容斥一手，使得 \(l,r\) 不连通。这样我们就可以枚举一个断点：

\[f_{l,r}=\sum_{i=l}^{r-1}f_{l,i}\times g_{i+1,r} \]

于是直接 \(O(n^3)\) 计算即可。

33 AGC023E Inversions

34 P3214 [HNOI2011]卡农

35 [2018雅礼集训1-16] 方阵

偶然碰到的一道题。

浅谈一些格路计数问题

posted @ 2021-11-02 08:55 xiaoziyao 阅读(203) 评论(1) 收藏举报

刷新页面返回顶部