亲爱的 解题报告

亲爱的 解题报告

简要题意

给定一个长度为 \(n\) 的字符串 \(s\)，字符集大小 \(62\)。询问有多少子序列满足：

• 长度为 \(6\)。
• 形式如同 \(ABCDCD\)。（其中 \(ABCD\) 为四个互不相同的字符）

数据范围：\(n \le 10^6\)。

分析

首先，我们注意到：第 \(3\) 个字符是特殊的。因为前两个字符只需要不同即刻，自己和后一个字符需要交替出现两次。因此我们枚举第 \(3\) 个字符的位置，枚举第 \(4\) 个字符是什么。

那么第 \(i\) 个位置的贡献为，前面的方案数乘上后面的方案数。

前面的方案数是好确定的：假如我们枚举到了第三个字符位置为 \(i\)，第四个字符为 \(c\)。就是所有可能的取法减去取了两个相同数的情况，也就是 \(\frac{i*(i-1)}{2}-\sum \limits_{i=1}^{62}\frac{cnt_i*(cnt_i-1)}{2}\)。然后还需要减去取了 \(s_i\) 和 \(c\) 的情况（留给读者思考）。

后面的方案数统计需要思考。

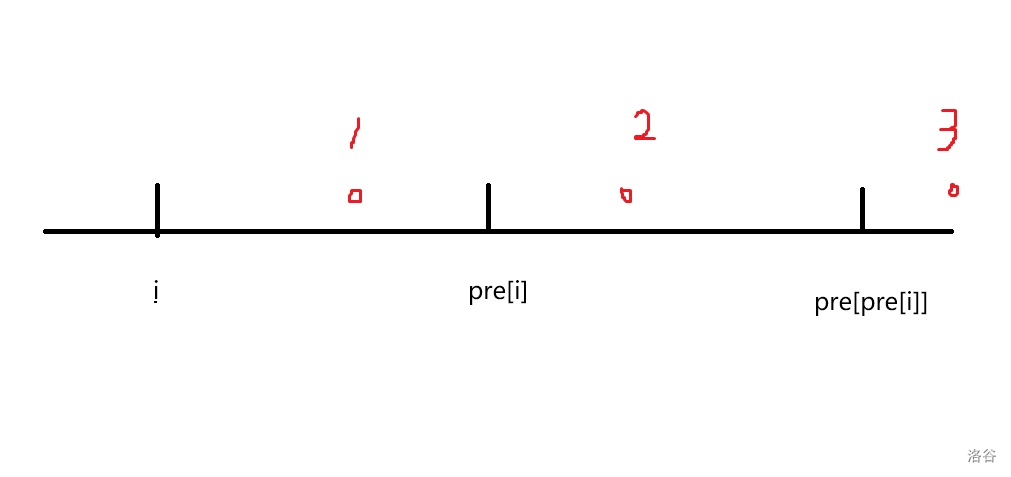
红色点表示 \(c\) 字符的出现位置，\(pre_i\) 表示 \(s_i\) 下一次出现的位置。

首先，\((2,3)\) 是可以贡献的，但是它已经在 \(pre_i\) 处被统计了，所以 \(i\) 处直接继承即可。也就是我们只需要维护在 \((i,pre_i)\) 内的字符的贡献即可。

然后我们我们看点对 \((1,3)\) 的贡献为 \(2\)，\((1,2)\) 的贡献为 \(1\)。为什么不同呢？因为他们间隔的字符 \(s_i\) 个数不同。

所以你需要维护一个字符是从后往前数第几次出现，令 \(t_{i,c}\) 表示位置 \(i\) 第一次被字符 \(c\) 统计时，\(c\) 的的出现次数。然后维护 \(\sum \limits_{i \le j,a_j=c}cnt_{j,c}\)。剩下的我就不赘述了。

时间复杂度 \(O(n|\sum|)\)。

如果有不懂的，在评论区问吧，有空会回的。

代码

const int N=1e5+100,M=70,K=62,mod=998244353;
int n,ans,a[N],ch[300],pre[N],lst[M],tr[N][M],bk[N][M],cnt[N],f[N][M],g[N][M];
char s[N];
int main()
{
//#if !ONLINE_JUDGE
    freopen("habibi.in","r",stdin);
    freopen("habibi.out","w",stdout);
//#endif 
    scanf("%s",s+1);
    n=strlen(s+1);
    For(i,1,26) ch[(int)'a'+i-1]=i;
    For(i,1,26) ch[(int)'A'+i-1]=i+26;
    For(i,1,10) ch[(int)'0'+i-1]=i+52;
    For(i,1,n) a[i]=ch[(int)s[i]];
    //预处理各种东西
    For(i,1,n){
        For(j,1,K) tr[i][j]=lst[j];
        lst[a[i]]=i; 
    }
    //return 0;
    For(i,1,K) lst[i]=n+1;
    Down(i,n,1){
        For(j,1,K) bk[i][j]=lst[j];
        pre[i]=lst[a[i]];
        cnt[i]=cnt[pre[i]]+1;
        lst[a[i]]=i;
    }
    For(i,1,K) lst[i]=0;
    //For(i,1,n) printf("%d ",cnt[i]);
    //putchar('\n');
    //求出 f 数组
    //f[i][j]: 表示当 a[i] 做第三个且 第四个为 j 时的方案数
    Down(i,n,1){
        if(!pre[i]) continue;
        int p=pre[i];
        For(j,1,K){
            if(j==a[i]) continue;
            f[i][j]=f[p][j];
            g[i][j]=g[p][j];
            if(i<=tr[p][j]){
                int u=bk[i][j],v=tr[p][j],tim=cnt[u]-cnt[v]+1;
                //printf("%d %d (%d,%d)\n",i,p,u,v);
                f[i][j]=bmod(1ll*f[i][j]+1ll*tim*(1ll*(cnt[v]-1)*cnt[p]-g[p][j])%mod);
                g[i][j]=bmod(1ll*g[i][j]+1ll*tim*cnt[p]);
            }
        }
    }
    //统计答案
    int tot=0;
    For(i,1,K) cnt[i]=0;
    tot=bmod(tot-cnt[a[1]]);
    ++cnt[a[1]];
    tot=bmod(tot+1-cnt[a[2]]);
    ++cnt[a[2]];
    For(i,3,n){
        int nw=tot;
        For(c,1,K)
                if(c!=a[i])
                    nw=bmod(1ll*nw-1ll*cnt[c]*cnt[a[i]]%mod+mod);
        For(j,1,K){
            if(j==a[i]) continue;
            //int nwtot=bmod(tot-cnt[a[i]]-cnt[j]+mod);
            int nwtot=nw;
            For(c,1,K)
                if(c!=j)
                    nwtot=bmod(1ll*nwtot-1ll*cnt[c]*cnt[j]%mod+mod);
            nwtot=bmod(1ll*nwtot+1ll*cnt[a[i]]*cnt[j]%mod);
            //if(nwtot*f[i][j]) printf("%d %d %d( %d ) %d\n",i,j,nwtot,tot,f[i][j]);
            ans=bmod(1ll*ans+1ll*nwtot*f[i][j]%mod);
        }
        tot=bmod(tot+i-1-cnt[a[i]]);
        ++cnt[a[i]];
    }
    /*For(i,1,n){
        For(j,1,K)
            printf("%d ",f[i][j]);
        putchar('\n');
    }*/
    printf("%d",ans);
    return 0;
}