PAM 学习笔记

一：初步认识

PAM，即回文自动机，是一个有限状态自动机。

接受状态为字符串中的所有回文子串。

二：构造

首先我们有一个结论：对于一个字符串 $s$，在 $s$ 后加入一个字符 $c$，字符串增加至多一个本质不同回文子串。

证明：

我们定义对于一个回文串 $t$，它的最长回文后缀为 $fail_t$；令 $s$ 的最长回文后缀为 $lst$；$|s|$ 表示字符串 $s$ 的长度；$s+t$ 表示将 $t$ 接在 $s$ 的后面。

在加入 $c$ 后，我们重复以下过程：

判断 $s_{|s|-|lst|-1}=c$ 是否成立；
如果成立，那么 $p \leftarrow lst$，退出。
如果不成立，那么 $lst \leftarrow fail_{lst}$，回到第一步。

对于 $p$，我们直接判断 $c+p+c$ 是否是一个新的回文子串。

同时，对于 $p$ 通过跳 $fail$ 可以访问到的所有字符串都不会产生新的回文子串。

这是因为：对于一个 $p$ 可以通过上述操作访问的节点 $q$，那么在字符串中这两个字符串的位置如图所示（请记住，$p$ 是一个回文串）：

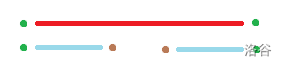
这是一张图片

其中红色线段表示 $p$，蓝色线段表示 $q$，绿色点表示 $c$，棕色点表示 $x$。（上下两部分表示的是同一个字符串）

因为 $p$ 满足 $s_{|s|-|p|-1}=c$，因此 $p$ 的左侧也有 $c$；因为 $p$ 是回文串，所以 $q$ 左侧的字符 $x$，也同时在 $p$ 的另一侧出现在 $q$ 的左侧。如果 $x=c$，那么 $x+q+c$ 是一个回文子串；但是在之前就已经有 $c+q+x$，因此这不是一个新的回文子串。

因此有且仅有 $p$ 有机会产生新的回文子串。

Q.E.D

那么上述过程也是 PAM 的构造方法。

我们约定：

$len_p$ 表示点 $p$ 对应字符串的长度；
$lst$ 表示插入前 $s$ 的最长回文后缀；
$tr_{p,c}$ 在 $p$ 的左右都加一个字符 $c$ 构成的回文串对应节点编号。

具体地，在加入一个新的字符 $c$ 时：

我们不断跳 $lst$ 的 $fail$ 指针直到找到一个点 $p$，满足 $s_{|s|-len_p-1}=c$。
如果 $tr_{p,c}$ 存在，那么直接 $lst \leftarrow tr_{p,c}$，退出。
如果不存在，那么我们就新建一个点 $cur$，$len_{cur} \leftarrow len_p+2,tr_{p,c} \leftarrow cur$。
此时我们要维护 $cur$ 的 $fail$，其实就是从 $p$ 继续跳 $fail$，直到找到一个点 $q$，满足 $s_{|s|-len_q-1}=c$，那么有 $fail_{cur} \leftarrow q$。
$lst \leftarrow tr_{p,c}$，退出。

那么有一个问题：怎么处理长度为 $1$ 或 $2$ 的回文子串呢？

这里有一个神奇的方法：len[1]=-1,fail[0]=1,len[1]=0。（其中 $1$ 节点可以理解为加入字符后构成的是长度为 $1$ 的空串，节点 $0$ 可以理解为加入字符后构成的是长度为 0$ 的空串）。

三：参考实现

选用例题（P3649 [APIO2014] 回文串)

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Inf (1ll<<60)
#define For(i,s,t) for(int i=s;i<=t;++i)
#define Down(i,s,t) for(int i=s;i>=t;--i)
#define ls (i<<1)
#define rs (i<<1|1)
#define bmod(x) ((x)>=mod?(x)-mod:(x))
#define add(x,y) (1ll*(x)+(y))%mod
#define lowbit(x) ((x)&(-(x)))
#define End {printf("NO\n");exit(0);}
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
inline void ckmx(int &x,int y){x=(x>y)?x:y;}
inline void ckmn(int &x,int y){x=(x<y)?x:y;}
inline void ckmx(ll &x,ll y){x=(x>y)?x:y;}
inline void ckmn(ll &x,ll y){x=(x<y)?x:y;}
inline int min(int x,int y){return x<y?x:y;}
inline int max(int x,int y){return x>y?x:y;}
inline ll min(ll x,ll y){return x<y?x:y;}
inline ll max(ll x,ll y){return x>y?x:y;}
inline int read(){
    register int x=0,f=1;
    char c=getchar();
    while(c<'0' || '9'<c) f=(c=='-')?-1:1,c=getchar();
    while('0'<=c && c<='9') x=(x<<1)+(x<<3)+c-'0',c=getchar();
    return x*f;
}
void write(int x){
    if(x>=10) write(x/10);
    putchar(x%10+'0');
}
const int N=3e5+100;
int n,m,len[N],fail[N],tr[N][26],lst,tot,occ[N];
ll ans;
char s[N];
int readstr(){
    int len=0;
    char c=getchar();
    while(c<'a' || 'z'<c) c=getchar();
    while('a'<=c && c<='z') s[++len]=c,c=getchar();
    return len;
}
int main()
{
#if !ONLINE_JUDGE
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
#endif 
    n=readstr();
    len[1]=-1,fail[0]=1,tot=1;
    For(i,1,n){
        int c=s[i]-'a',p=lst;
        while(s[i-len[p]-1]!=s[i]) p=fail[p];
        if(!tr[p][c]){
            int q=++tot,nxt;
            len[q]=len[p]+2;
            nxt=fail[p];
            while(s[i-len[nxt]-1]!=s[i]) nxt=fail[nxt];
            fail[q]=tr[nxt][c];
            tr[p][c]=q;
        }
        lst=tr[p][c];
        ++occ[lst];
    }
    Down(i,tot,1)
        ans=max(ans,1ll*occ[i]*len[i]),occ[fail[i]]+=occ[i];
    printf("%lld",ans);
    return 0;
}

四：时间复杂度证明

设 $lst$ 可以跳 $fail$ 的次数为 $dep$。

此时我们看到 $dep$ 变化的位置：

while(s[i-len[p]-1]!=s[i]) p=fail[p]; 这里每进行一次 $dep$ 减一，因为后续有 lst=tr[p][c]。
while(s[i-len[nxt]-1]!=s[i]) nxt=fail[nxt]; 这里每进行一次 $dep$ 减一，因为后续有 lst=tr[p][c]。
lst=tr[p][c]; 这里 $dep$ 至多加二，因为 $fail_{p}$ 的长度至多加二，也就是至多可以再多跳两次（每一次跳 $fail$ ，字符串长度至少减一）。

故时间复杂度线性。

posted @ 2025-08-24 12:58 XiaoZi_qwq 阅读(8) 评论(0) 收藏举报

刷新页面返回顶部

xiaozi-qwq

PAM 学习笔记