最大团 解题报告

题目描述

给出平面上 \(n\) 个点，并且平面上有一个以原点为圆心，半径为 \(r\) 的圆。我们认为两个点之间有边，当且仅当这两个点连成的直线和圆不相交（保证不存在两点构成的直线与圆相切）。求此图的最大团。

数据范围：\(n \le 2\times 10^3\)，输入中的数据均为整数，且绝对值小于等于 \(5 \times 10^3\)。

分析

首先做一步转化：对于平面上的任意两个点，如果它们连成的直线和以原点为圆心的圆无交，当且仅当这两个点分别对圆做切线，切点构成的劣弧有交且互不包含。

证明可以自行画图体会。

然后有一个补充：对于上述区间，对任意若干个区间取补集，结论仍旧成立。（反证法容易证明）

然后问题转化为：给定若干区间，选出最多的区间使得所有区间互相有交且互不包含。

先考虑刻画“互不包含“的条件：对于互不包含的两个区间 \([l_1,r_1][l_2,r_2]\),如果存在 \(l_1 \le l_2\)，那么肯定存在 \(r_1 \le r_2\)，那么只需要对左端点进行排序，对右端点求 LIS 即可。

再考虑刻画“有交”的条件：考虑左端点最小的区间，所有被选的区间都和它有交，因此只需要对左端点在这个区间内的区间做上述操作即可。

关于求切点构成的区间：

我们以一个向量 \(\vec{a}=(x,y)\) 为例。

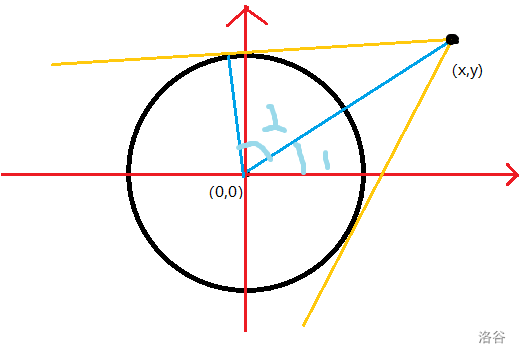
首先我们可以先求 \(\angle 1\)，容易发现 \(\tan \angle 1=\frac{x}{y}\)，那么 \(\angle 1 =\arctan\frac{x}{y}\)。

同理，\(\angle 2=arccos \frac{r}{|a|}\)。

然后简单加减即可。

代码

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Inf (1ll<<60)
#define For(i,s,t) for(int i=s;i<=t;++i)
#define Down(i,s,t) for(int i=s;i>=t;--i)
#define ls (i<<1)
#define rs (i<<1|1)
#define bmod(x) ((x)>=mod?(x)-mod:(x))
#define lowbit(x) ((x)&(-(x)))
#define End {printf("NO\n");exit(0);}
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
inline void ckmx(int &x,int y){x=(x>y)?x:y;}
inline void ckmn(int &x,int y){x=(x<y)?x:y;}
inline void ckmx(ll &x,ll y){x=(x>y)?x:y;}
inline void ckmn(ll &x,ll y){x=(x<y)?x:y;}
inline int min(int x,int y){return x<y?x:y;}
inline int max(int x,int y){return x>y?x:y;}
inline ll min(ll x,ll y){return x<y?x:y;}
inline ll max(ll x,ll y){return x>y?x:y;}
inline int read(){
    register int x=0,f=1;
    char c=getchar();
    while(c<'0' || '9'<c) f=(c=='-')?-1:1,c=getchar();
    while('0'<=c && c<='9') x=(x<<1)+(x<<3)+c-'0',c=getchar();
    return x*f;
}
void write(int x){
    if(x>=10) write(x/10);
    putchar(x%10+'0');
}
const int N=2e3+100;
const double Pi=acos(-1);
int n,r;
double angle1[N],angle2[N];
struct Point{double x,y;}p[N];
#define pow(x) ((x)*(x))
double getlen(Point x){return sqrt(pow(x.x)+pow(x.y));}
struct Node{double l,r;}a[N],b[N];
bool cmp(Node x,Node y){return x.l<y.l;}
int len,m,ans;
double f[N];
int Lis(){
    f[0]=-Pi-1,len=0;
    For(i,1,m){
        if(b[i].r>f[len]){
            f[++len]=b[i].r;
            continue;
        }
        int L=0,R=len,mid,res=0;
        while(L<=R){
            mid=L+R>>1;
            if(f[mid]<b[i].r)
                res=mid,L=mid+1;
            else
                R=mid-1;
        }
        f[res+1]=min(f[res+1],b[i].r);
    }
    return len;
}
int main()
{
    freopen("clique.in","r",stdin);
    freopen("clique.out","w",stdout);
    n=read(),r=read();
    For(i,1,n) p[i].x=read(),p[i].y=read();
    For(i,1,n){
        angle1[i]=atan2(p[i].y,p[i].x);
        angle2[i]=acos(1.0*r/getlen(p[i]));
        a[i].l=angle1[i]-angle2[i];
        a[i].r=angle1[i]+angle2[i];
        if(a[i].l<-Pi) a[i].l+=2*Pi;
        if(a[i].r>Pi) a[i].r-=2*Pi;
        if(a[i].l>a[i].r) swap(a[i].l,a[i].r);
        //printf("%0.3lf %0.3lf %0.3lf %0.3lf %0.3lf\n",angle1[i],angle2[i],a[i].l,a[i].r,Pi);
    }
    //assert(false);
    For(i,1,n){
        m=0;
        b[++m]=a[i];
        For(j,1,n)
            if(a[i].l<a[j].l && a[j].l<a[i].r && a[j].r>a[i].r && i!=j)
                b[++m]=a[j];
        sort(b+1,b+m+1,cmp);
        ckmx(ans,Lis());
    }
    printf("%d\n",ans);
    return 0;
}