树的合并 解题报告

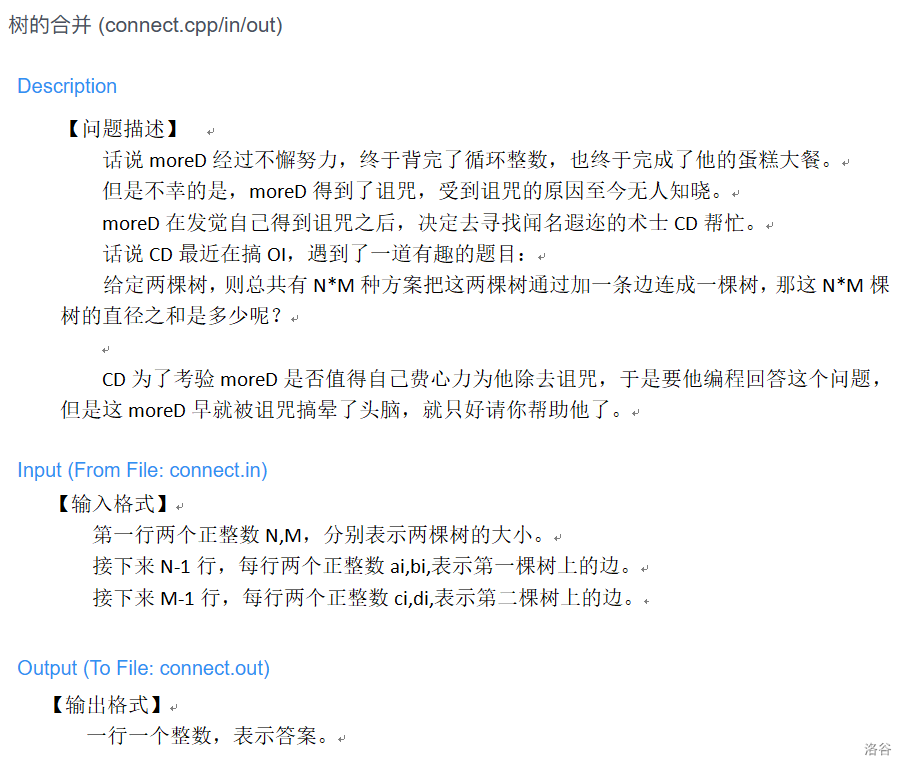
刚看题先想暴力，枚举每一种加边，求一次直径，时间复杂度 \(O(N*M*(N+M))\)
但可以马上想到，加边前，答案为两棵树中较长的直径（记为 \(len\)）；在加边 \((u,v)\) 后，如果直径变化，那么新的直径一定包含新加的那条边；而且，我们在加边前可以预处理出每一个点可以延伸的最长链的长度 \(f_i\),那么此时的直径长度就是\(max(len,f_u+1+f_v)\)，时间复杂度 \(O(n*m)\)
深入思考后可以发现，加边后直径会变化，当且仅当 \(f_u+f_v+1>len\)，变形可得 \(f_u>len-f_v-1\)，所以我们只需要维护两个前缀和 \(d_i\) 和 \(val_i\)，分别表示 \(f_i\) 小于等于 \(i\) 的点的个数和 \(f_i\) 的和。最后计算即可。

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int N=1e5+100;
int n,m,f[N],g[N],d[N],t[N],len;
ll ans,val[N];
struct Edge{int from,to;}e[N<<1];
int num,h[N];
void add(int f,int t){e[++num].from=h[f],e[num].to=t,h[f]=num;}
void dfs(int u,int fa){
  f[u]=0;
  for(int i=h[u];i;i=e[i].from)
    if(e[i].to!=fa)
      dfs(e[i].to,u),f[u]=max(f[u],f[e[i].to]+1);
}
void dfs1(int u,int fa,int lst){
  int mx0,mx1;
  mx1=mx0=-1;
  g[u]=max(lst,f[u]);
  for(int i=h[u],v;i;i=e[i].from){
    v=e[i].to;
    if(v==fa) continue;
    if(f[v]>mx0) mx1=mx0,mx0=f[v];
    else if(f[v]>mx1) mx1=f[v];
  }
  for(int i=h[u];i;i=e[i].from){
    if(e[i].to==fa) continue;
    if(f[e[i].to]==mx0)
      dfs1(e[i].to,u,max(mx1+1,lst)+1);
    else
      dfs1(e[i].to,u,max(mx0+1,lst)+1);
  }
}
int main()
{
  freopen("connect.in","r",stdin);
  freopen("connect.out","w",stdout);
  scanf("%d%d",&n,&m);
  for(int i=1,u,v;i<n;i++) scanf("%d%d",&u,&v),add(u,v),add(v,u);
  dfs(1,0);
  dfs1(1,0,0);
  //g[1]=f[1];
  for(int i=1;i<=n;i++) t[g[i]]++,len=max(len,g[i]);
  for(int i=1;i<=n;i++) d[i]=d[i-1]+t[i],val[i]=val[i-1]+1ll*t[i]*i;
  num=0;memset(h,0,sizeof(h));memset(f,0,sizeof(f)),memset(g,0,sizeof(g));
  swap(n,m);
  for(int i=1,u,v;i<n;i++) scanf("%d%d",&u,&v),add(u,v),add(v,u);
  dfs(1,0);
  dfs1(1,0,0);
  //g[1]=f[1];
  for(int i=1;i<=n;i++) len=max(len,g[i]);
  for(int i=1;i<=n;i++)
    ans+=1ll*(g[i]+1)*(m-d[max(len-g[i]-1,0)])+1ll*len*d[max(len-g[i]-1,0)]+(val[m]-val[max(len-g[i]-1,0)]);
  printf("%lld",ans);
  return 0;
}