自注意力机制

针对输入是一组向量，输出也是一组向量，输入长度为N的向量，输出同样为长度为N的向量。

单个输出

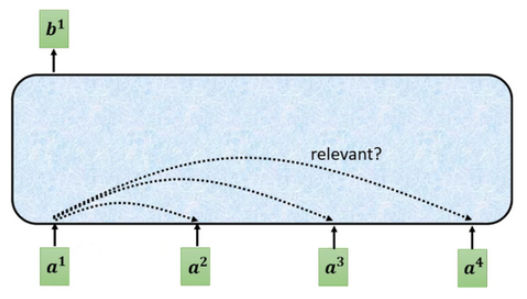
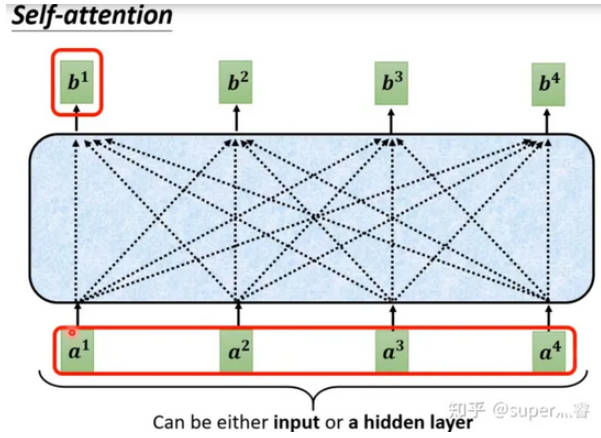
对于每一个输入向量a，经过蓝色部分self-attention之后都输出一个向量b，这个向量是考虑了所有的输入向量对a1产生的影响才得到的，这里有四个词向量a对应就会输出四个向量b。

下面以b1的输出为例

首先，计算sequence中各向量与a1的关联程度，有下面两种方法

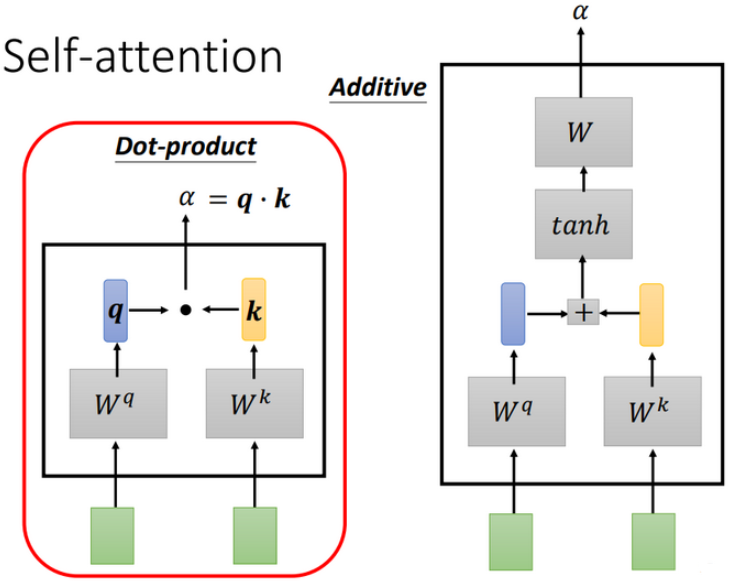
Dot-product方法是将两个向量乘上不同的矩阵w，得到q和k，做点积得到$\alpha$，transformer中就用到了Dot-product。

上图中绿色的部分就是输入向量a1和a2，灰色的Wq和Wk为权重矩阵，需要学习来更新，用a1去和Wq相乘，得到一个向量q，然后使用a2和wk相乘，得到一个数值k。最后使用q和k做点积，得到$\alpha$。$\alpha$也就是表示两个向量之间的相关联程度。

上图右边加性模型这种机制也是输入向量与权重矩阵相乘，后相加，然后使用$\tanh$投射到一个新的函数空间内，再与权重矩阵相乘，得到最后的结果。

计算每一个$\alpha$（又称为attention score），q称为query，k称为key

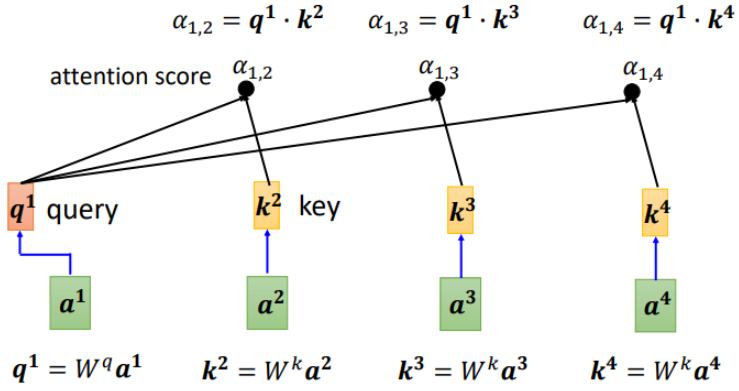
另外，也可以计算a1和自己的关联性，再得到各向量与a1的相关程度之后，用softmax计算出一个attention distribution，这样就把相关程度归一化，通过数值就可以看出哪些向量是和a1最有关系。

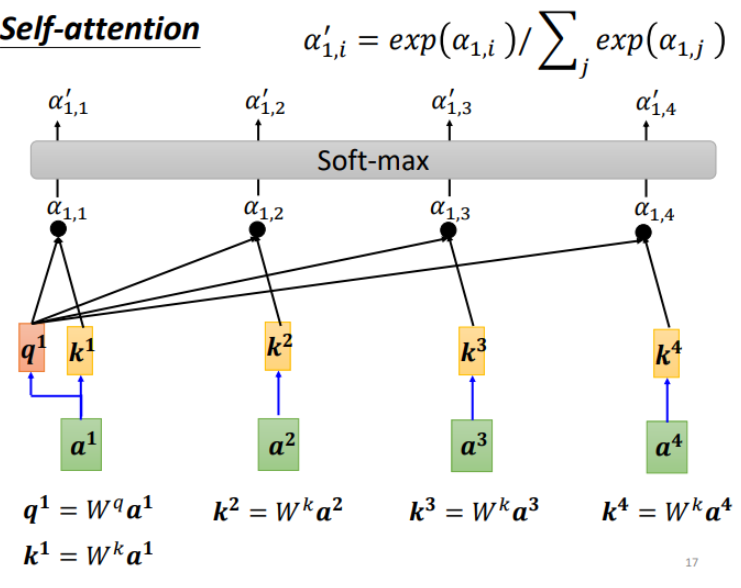
下面需要根据$\alpha'$抽取sequence里重要的信息：

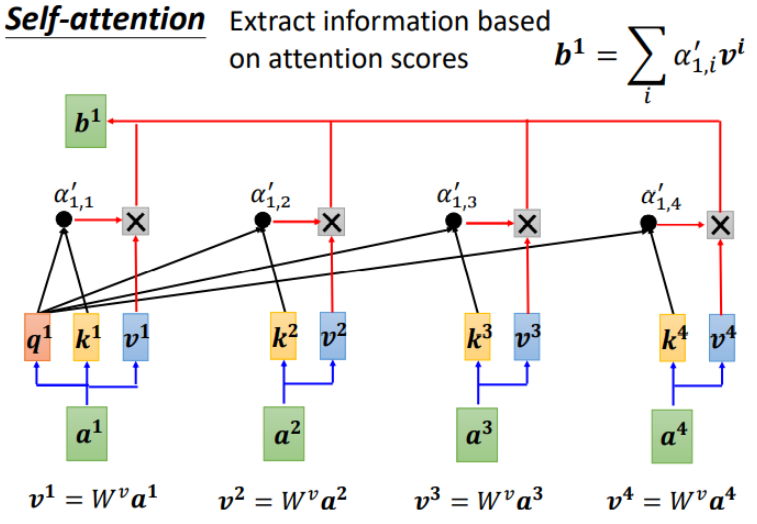
先求v，v就是键值value，v和q、k计算方式相同，也是用输入a乘以权重矩阵W，得到v后，与对应的$\alpha'$相乘，每个v乘和$\alpha'$后求和，得到输出的b1。如果a1和a2关联性比较高，$\alpha'_{1,2}$就比较大，那么，得到的输出b1就可能比较接近v2，即attention score决定了该vector在结果中占的分量。

矩阵运算

用矩阵运算表示b1的生成：

step 1：q、k、v的矩阵形式生成

\[q^i = w^q \cdot a^i \]

\[k^i = w^k \cdot a^i \]

\[v^i = w^v \cdot a^i \]

写成矩阵形式：

\[Q = W^q \cdot I \]

\[K = W^k \cdot I \]

\[V = W^v \cdot I \]

把4个输入$a$拼成一个矩阵$I$，这个矩阵有4个column，也就是$a1$到$a4$,$I$乘上相应的权重矩阵$W$，得到相应的矩阵$Q$、$K$、$V$，分别表示query, key 和value。

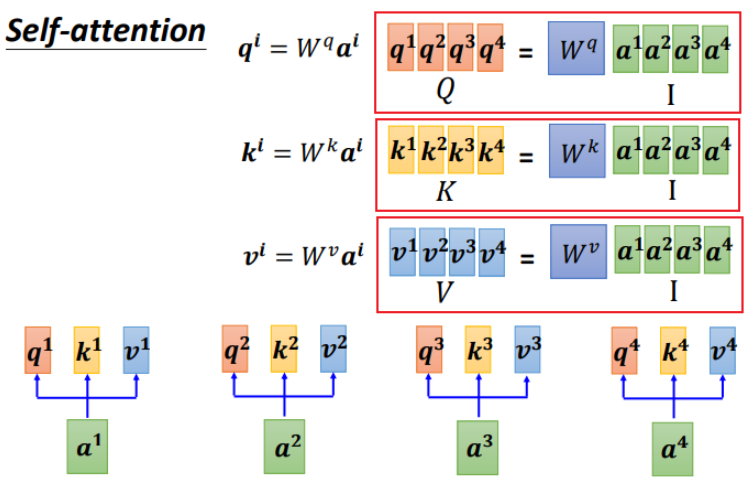
三个$W$是我们需要学习的参数

step 2：利用得到的$Q$和$K$计算每两个输入向量之间的相关性，也就是计算attention的值$\alpha$，$\alpha$的计算方法有多种，通常采用点乘的方式。先针对$q1$，通过与$k1$到$k4$拼接成的矩阵$K$相乘，得到$\alpha_{1,n}$拼接成矩阵。

同样，$q1$到$q4$也可以拼接成矩阵$Q$直接与矩阵$K$相乘：

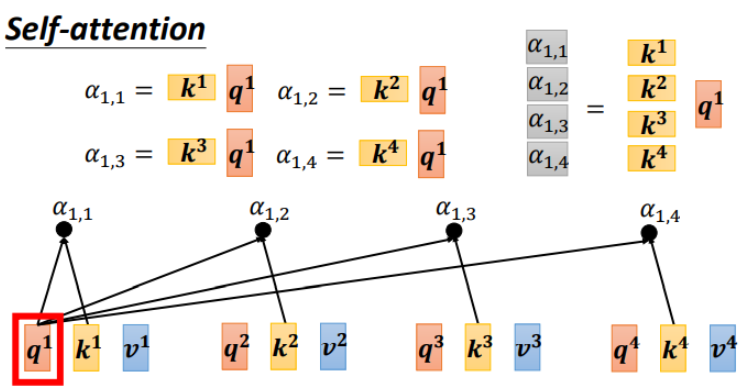
公式为：

\[\alpha_{i,j} = (q^i)^\tau \cdot k^j \]

矩阵形式：

\[A = K^T \cdot Q \]

矩阵中的每一个值记录了对应的两个输入向量的attention的大小$\alpha$，$A'$是经过softmax归一化后的矩阵。

step 3：得到$A'$和$V$，计算每个输入向量$a$对应的self-attention层的输出向量b：

\[b_i = \sum_{j=1}^{n}v_i \cdot \alpha'_{i,j} \]

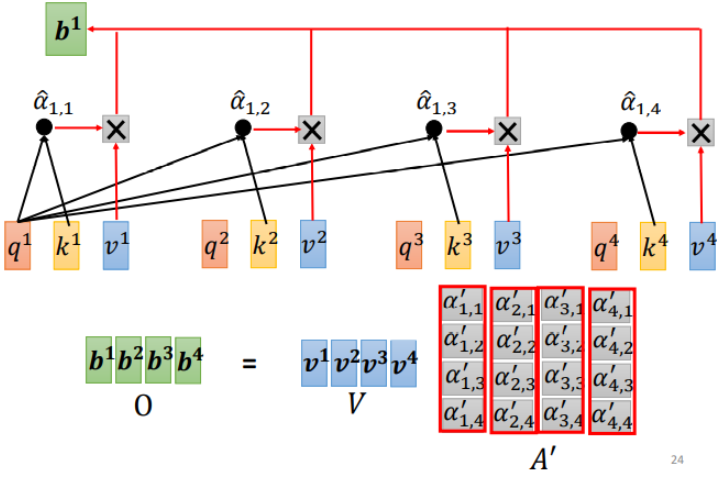
写成矩阵形式：

\[O = V \cdot A' \]

self-attention 总结

输入为$I$，输出为$O$:

矩阵$W^q,W^k,W^v $是需要学习的参数。

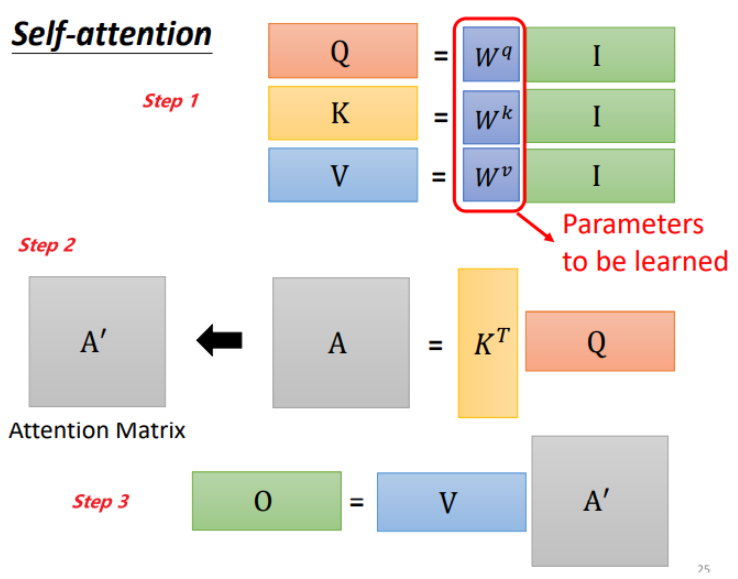
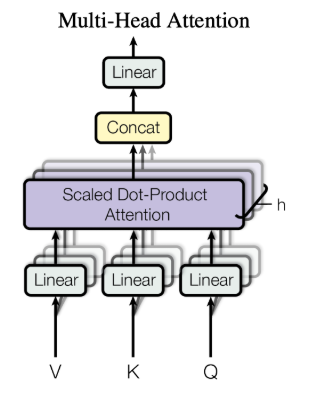
多头自注意力机制

自注意力机制的进阶版本是多头自注意力机制。
因为相关性有很多不同的形式，有很多不同的定义，所以有时不能只有一个$q$，要有多个$q$，不同的$q$负责不同种类的相关性。

对于一个输入$a$

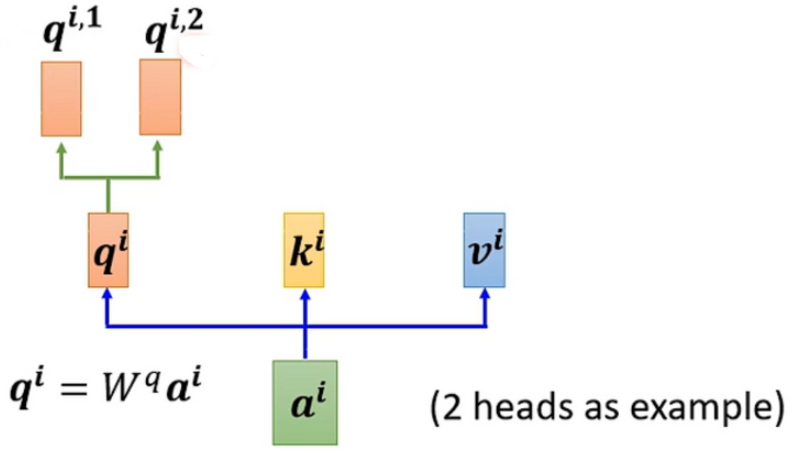
首先，和上面一样，用$a$乘权重矩阵$W$得到$q^i$，然后再用$q^i$乘两个不同的$W$，得到两个不同的$q^{i,n}$，$i$代表的是位置，1和2代表的是这个位置的第几个$q$。

\[q^{i,1} = W^{q,1}q^i \]

\[q^{i,2} = W^{q,2}q^i \]

上面这个图中，有两个head，代表这个问题有两种不同的相关性。

同样，$k$和$v$也需要有多个，两个$k,v$的计算方式和$q$相同，都是先计算出来$k^i$和$v^i$，然后再乘两个不同的权重矩阵。

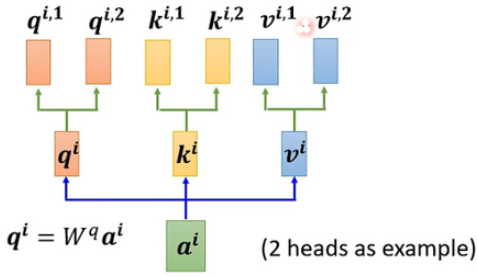
对于多个输入向量也一样，每个向量都有多个head:

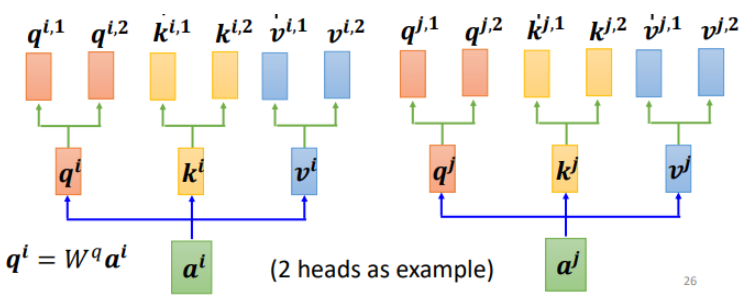
算出来$q,k,v$ 之后怎么做self-attention呢？

和上面讲的过程一样，只不过是1那类的一起做，2那类的一起做，两个独立的过程，算出来两个b。

对于1：

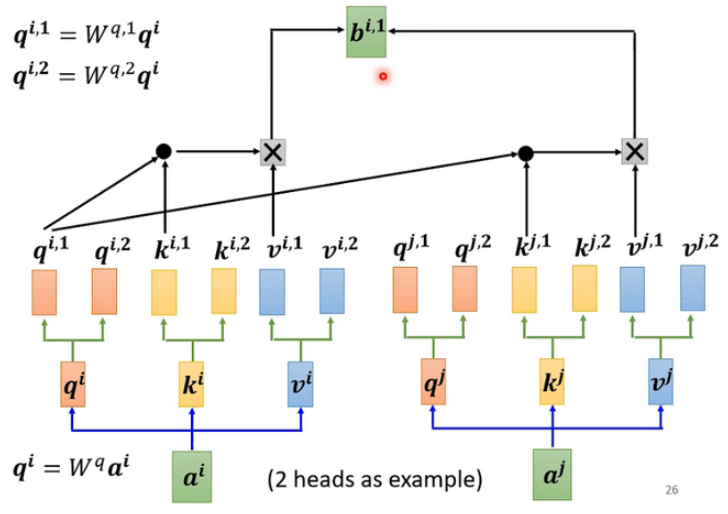
对于2：

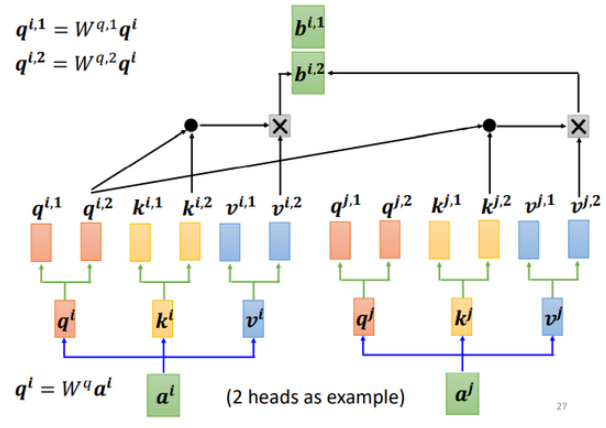
这只是两个head的例子，有多个head过程也一样，都是分开算b。
最后，把$b^{i,1},b^{i,2}$拼接成矩阵再乘权重矩阵$W$，得到$b^i$，也就是这个self-attention向量$b^i$的输出，如下图所示：

positional encoding

在训练self-attention的时候，实际上对于位置的信息是缺失的，没有前后的区别，上面讲的$a1,a2,a3$不代表输入的顺序，只是指输入的向量数量，不像$RNN$，对于输入有明显的前后顺序，比如在翻译任务里面，对于“机器学习”，机器学习依次输入。而self-attention的输入是同时输入，输出也是同时产生然后输出的。

如何在self-attention里面体现位置信息呢？就是使用Positional Encoding。

也就是新引入一个位置向量$e^i$，非常简单，如下图所示：

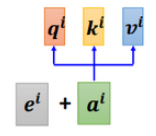
每个位置设置一个vector，叫做positional vector，用$e^i$表示，不同的位置有一个专属的$e^i$。
如果$a^i$加上了$e^i$，就会体现出位置的信息，$i$是多少，位置就是多少。
vector长度是认为设定的，也可以从数据中训练出来。

代码

import torch
import torch.nn as nn
import torch.nn.functional as F

class MultiHeadAttention(nn.Module):
 def __init__(self, in_dim, k_dim, v_dim, num_heads):
     super(MultiHeadAttention, self).__init__()
     self.num_heads = num_heads
     self.k_dim = k_dim
     self.v_dim = v_dim
     
     # 定义线性投影层，用于将输入变换到多头注意力空间
     self.proj_q = nn.Linear(in_dim, k_dim * num_heads, bias=False)
     self.proj_k = nn.Linear(in_dim, k_dim * num_heads, bias=False)
     self.proj_v = nn.Linear(in_dim, v_dim * num_heads, bias=False)
 	# 定义多头注意力的线性输出层
     self.proj_o = nn.Linear(v_dim * num_heads, in_dim)
     
 def forward(self, x, mask=None):
     batch_size, seq_len, in_dim = x.size()
     # 对输入进行线性投影, 将每个头的查询、键、值进行切分和拼接
     q = self.proj_q(x).view(batch_size, seq_len, self.num_heads, self.k_dim).permute(0, 2, 1, 3)
     k = self.proj_k(x).view(batch_size, seq_len, self.num_heads, self.k_dim).permute(0, 2, 3, 1)
     v = self.proj_v(x).view(batch_size, seq_len, self.num_heads, self.v_dim).permute(0, 2, 1, 3)
     # 计算注意力权重和输出结果
     attn = torch.matmul(q, k) / self.k_dim**0.5   # 注意力得分
     
     if mask is not None:
         attn = attn.masked_fill(mask == 0, -1e9)
     
     attn = F.softmax(attn, dim=-1)   # 注意力权重参数
     output = torch.matmul(attn, v).permute(0, 2, 1, 3).contiguous().view(batch_size, seq_len, -1)   # 输出结果
     # 对多头注意力输出进行线性变换和输出
     output = self.proj_o(output)
     
     return output

class CrossAttention(nn.Module):
 def __init__(self, in_dim1, in_dim2, k_dim, v_dim, num_heads):
     super(CrossAttention, self).__init__()
     self.num_heads = num_heads
     self.k_dim = k_dim
     self.v_dim = v_dim
     
     self.proj_q1 = nn.Linear(in_dim1, k_dim * num_heads, bias=False)
     self.proj_k2 = nn.Linear(in_dim2, k_dim * num_heads, bias=False)
     self.proj_v2 = nn.Linear(in_dim2, v_dim * num_heads, bias=False)
     self.proj_o = nn.Linear(v_dim * num_heads, in_dim1)
     
 def forward(self, x1, x2, mask=None):
     batch_size, seq_len1, in_dim1 = x1.size()
     seq_len2 = x2.size(1)
     
     q1 = self.proj_q1(x1).view(batch_size, seq_len1, self.num_heads, self.k_dim).permute(0, 2, 1, 3)
     k2 = self.proj_k2(x2).view(batch_size, seq_len2, self.num_heads, self.k_dim).permute(0, 2, 3, 1)
     v2 = self.proj_v2(x2).view(batch_size, seq_len2, self.num_heads, self.v_dim).permute(0, 2, 1, 3)
     
     attn = torch.matmul(q1, k2) / self.k_dim**0.5
     
     if mask is not None:
         attn = attn.masked_fill(mask == 0, -1e9)
     
     attn = F.softmax(attn, dim=-1)
     output = torch.matmul(attn, v2).permute(0, 2, 1, 3).contiguous().view(batch_size, seq_len1, -1)
     output = self.proj_o(output)
     return output

参考博客：
https://www.cnblogs.com/emanlee/p/17133700.html
https://blog.csdn.net/Michale_L/article/details/126549946
https://blog.csdn.net/qq_39506862/article/details/133868090

posted @ 2025-02-18 22:09 小舟渡河阅读(52) 评论(0) 收藏举报

刷新页面返回顶部

自注意力机制