第二次博客作业
第二次博客作业
前言:
经过几次大作业的“洗礼”——从简单的点线面到现在的三四五边形的各种计算,从比较轻松的通过到揪头发找测试点。我更是知道了清晰的逻辑和规范的代码书写是有多么重要,这几次的大作业让我知道自己以前的书写(代码)的方式是有多么烂。。。
感谢遇见,阿门!
接下来就是回顾和总结一下我那不堪回首的过去。
1:7-2 点线形系列4-凸四边形的计算
用户输入一组选项和数据,进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入四个点坐标,判断是否是四边形、平行四边形,判断结果输出true/false,结果之间以一个英文空格符分隔。
2:输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
3:输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
4:输入六个点坐标,前两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况:假设三角形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
\2) 不符合要求的输入:z 不与xy都相邻,如z x y s、x z s y、x s z y
5:输入五个点坐标,输出第一个是否在后四个点所构成的四边形(限定为凸四边形,不考虑凹四边形)或三角形(判定方法见选项4)的内部(若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。如果点在多边形的某条边上,输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形,输出"not a quadrilateral or triangle"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
选项1、2、3中,若四边形四个点中有重合点,输出"points coincide"。
选项4中,若前两个输入线的点重合,输出"points coincide"。
输入样例1:
选项1,点重合。例如:
1:-1,-1 -1,-1 1,2 1,-2
输出样例:
在这里给出相应的输出。例如:
points coincide
输入样例2:
不符合基本格式。例如:
1:-1,-1 1,2 -1,1 ++1,0
输出样例:
在这里给出相应的输出。例如:
Wrong Format
输入样例3:
选项1,输入点数量不对。例如:
1:-1,-1 -1,2
输出样例:
在这里给出相应的输出。例如:
wrong number of points
输入样例4:
选项1,正确输入判断。例如:
1:-1,-1 -1,1 1,2 1,-2
输出样例:
在这里给出相应的输出。例如:
true false
输入样例5:
选项2,输入点不构成四边形。例如:
2:10,10 1,1 0,0 1,20
输出样例:
在这里给出相应的输出。例如:
not a quadrilateral
输入样例6:
选项2,正方形。例如:
2:0,0 0,80 80,80 80,0
输出样例:
在这里给出相应的输出。例如:
true true true
输入样例7:
选项2。例如:
2:0,0 -10,80 0,160 -10,80
输出样例:
在这里给出相应的输出。例如:
not a quadrilateral
输入样例8:
选项3,凸四边形。例如:
3:-1,-1 -1,1 1,2 1,-2
输出样例:
在这里给出相应的输出。例如:
true 10.472 6.0
输入样例9:
选项3,。例如:
3:0,0 -10,100 0,99 10,100
输出样例:
在这里给出相应的输出。例如:
false 221.097 990.0
解题思路:
1:首先需要面临的问题就是如何判断是否是四边形:
a:首先四个点没有重和
b:输入的相邻的边不相交
c:输入的对边不相交,或者说是:对边平行或者交点不在线段上
2:其次是怎么判断四边形的凹凸性:
这里我用的是向量的方式,临边两两计算向量积,出现异号结果则出现凹点(为凹四边形)
3:直线与四边形的交点及两个交点情况下输出面积:
这里主要是注意交点是不是与输入的四个点(也就是四个顶点)出现重合的情况
4:点与四边形的关系:
我是没有用要求的射线法,而是使用面积的方式,毕竟上面已经有求面积的方法了。
以下是部分代码和代码的分析:
这里的四边形与直线的部分不是全通过,分析直线与四边形的关系的时候出错了
class SiBianXing//不是英文属于是有点不太好,别介意哈,后面的作业改了,知错了。
{
Points D1,D2,D3,D4;
Lines L1,L2,L3,L4;
Trianges T1,T2,T3,T4;
Trianges Tmax,Tm;
SiBianXing(Points p1,Points p2,Points p3,Points p4)
{
D1 = p1;
D2 = p2;
D3 = p3;
D4 = p4;
L1 = new Lines(p1,p2);
L2 = new Lines(p2,p3);
L3 = new Lines(p3,p4);
L4 = new Lines(p1,p4);
T1 = new Trianges(p1,p2,p4);
T2 = new Trianges(p2,p1,p3);
T3 = new Trianges(p3,p2,p4);
T4 = new Trianges(p4,p3,p1);
}
public boolean LinBianBuJiao()
{
if(!L2.LinesToLines(L4))
{
Points p = new Points((L2.GetXCusp(L4)),(L2.GetYCusp(L4)));
if(L2.CuoPiontOnLine(p)&&L4.CuoPiontOnLine(p)) //可以在一条线的线段内,不能在两条线的线段内(一开始的||错了,改成&&,下面同是)
{
return false;
}
}
if(!L1.LinesToLines(L3))
{
Points p = new Points((L1.GetXCusp(L3)),(L1.GetYCusp(L3)));
if(L1.CuoPiontOnLine(p)&&L3.CuoPiontOnLine(p))
{
return false;
}
}
return true;
}
public boolean IsSiBianXing() //判断是否是四边形,返回Boolean(true,false)
{
if(T2.IsTrianges()&&LinBianBuJiao())
{
if(T2.L1.GetPointsToLines(D4) != 0&&T2.L2.GetPointsToLines(D4) != 0&&T2.L3.GetPointsToLines(D4) != 0)
{
return true;
}
else
{
return false;
}
}
else
{
return false;
}
}
public boolean IsPXSBX() //是否是平行四边形,返回Boolean(true,false)
{
double l1 = L1.GetLength(),l2 = L3.GetLength();
if(l1 == l2&&((L1.D1.x==L1.D2.x&&L3.D1.x==L3.D2.x)||L1.LinesToLines(L3)))
{
return true;
}
else
{
return false;
}
}
public boolean IsLX()
{
if(L1.GetLength()==L2.GetLength()&&L1.GetLength()==L3.GetLength()&&L1.GetLength()==L4.GetLength()&&L2.GetLength()==L3.GetLength()&&L2.GetLength()==L4.GetLength()&&L3.GetLength()==L4.GetLength())
{
return true;
}
else
{
return false;
}
}
public boolean IsJX()
{
if(T1.IsZhiJiao()&&T2.IsZhiJiao()&&T3.IsZhiJiao())
{
return true;
}
else
{
return false;
}
}
public boolean IsZFX()
{
if(this.IsJX()&&this.IsLX())
{
return true;
}
else
{
return false;
}
}
public boolean IsTuSBX()
{
Lines l1 = new Lines(D1,D3);
Lines l2 = new Lines(D2,D4);
Points p = new Points(l1.GetXCusp(l2),l1.GetYCusp(l2));
if(l1.CuoPiontOnLine(p)&&l2.CuoPiontOnLine(p))
{
return true;
}
else
{
return false;
}
}
public double GetMianJi()
{
double m = 0;
if(this.IsTuSBX())
{
m = T1.GetMianJi()+T3.GetMianJi();
}
else
{
if(D1.PointsEqualPoints(this.FineAoDian()))
{
m = T2.GetMianJi()+T4.GetMianJi();
}
else
{
m = T1.GetMianJi()+T3.GetMianJi();
}
}
return m;
}
public Points FineAoDian() //用点到直线的距离(不带绝对值符号)用其中两个(D1和D3或者D2和D4)构成的线,求剩余两点到直线距离,如果d1*d2>0则找到凹点
{
Lines l1 = new Lines(D1,D3);
Lines l2 = new Lines(D2,D4);
double dl21 = (l1.A*D2.x+l1.B*D2.y+l1.C)/Math.pow(l1.A*l1.A+l1.B*l1.B, 0.5);
double dl41 = (l1.A*D4.x+l1.B*D4.y+l1.C)/Math.pow(l1.A*l1.A+l1.B*l1.B, 0.5);
double dl12 = (l2.A*D1.x+l2.B*D1.y+l2.C)/Math.pow(l2.A*l2.A+l2.B*l2.B, 0.5);
double dl32 = (l2.A*D3.x+l2.B*D3.y+l2.C)/Math.pow(l2.A*l2.A+l2.B*l2.B, 0.5);
if(dl21*dl41>0)
{
return D2;
}
else
{
return D1;
}
}
public double GetZhouChang()
{
double l = L1.GetLength()+L2.GetLength()+L3.GetLength()+L4.GetLength();
return l;
}
public void GetLineWithSiBianXing(Lines l)
{
Points[] cp =new Points[4];
int cpnum = 0;
if(l.LineCoincideLine(L1)||l.LineCoincideLine(L2)||l.LineCoincideLine(L3)||l.LineCoincideLine(L4))
{
System.out.println("The line is coincide with one of the lines");
return ;
}
if(this.L1.HaveCupsToLines(l))
{
Points cp1 = this.L1.GetCupsToLines(l);
if(this.L1.CuoPiontOnLine(cp1))
{
cp[cpnum] = cp1;
cpnum++;
}
}
if(this.L2.HaveCupsToLines(l))
{
Points cp2 = this.L2.GetCupsToLines(l);
if(this.L2.CuoPiontOnLine(cp2))
{
if((cpnum==1&&!cp2.PointsEqualPoints(cp[0]))||cpnum==0)
{
cp[cpnum] = cp2;
cpnum++;
}
}
}
if(this.L3.HaveCupsToLines(l))
{
Points cp3 = this.L3.GetCupsToLines(l);
if(this.L3.CuoPiontOnLine(cp3))
{
if((cpnum==2&&!cp3.PointsEqualPoints(cp[0])&&!cp3.PointsEqualPoints(cp[1]))||(cpnum==1&&!cp3.PointsEqualPoints(cp[0]))||cpnum==0)
{
cp[cpnum] = cp3;
cpnum++;
}
}
}
if(this.L4.HaveCupsToLines(l))
{
Points cp4 = this.L4.GetCupsToLines(l);
if(this.L4.CuoPiontOnLine(cp4))
{
if((cpnum==3&&!cp4.PointsEqualPoints(cp[2])&&!cp4.PointsEqualPoints(cp[0])&&!cp4.PointsEqualPoints(cp[1]))||(cpnum==2&&!cp4.PointsEqualPoints(cp[0])&&!cp4.PointsEqualPoints(cp[1]))||(cpnum==1&&!cp4.PointsEqualPoints(cp[0]))||cpnum==0)
{
cp[cpnum] = cp4;
cpnum++;
}
}
}
if(cpnum!=2)
{
System.out.println(cpnum);
}
else
{
Lines lcup = new Lines(cp[0],cp[1]);
Points[] cpz = new Points[4];
Points[] cpy = new Points[4];
int cpznum =0;
int cpynum =0;
double dl1 = (lcup.A*D1.x+lcup.B*D1.y+lcup.C)/Math.pow(lcup.A*lcup.A+lcup.B*lcup.B, 0.5);
double dl2 = (lcup.A*D2.x+lcup.B*D2.y+lcup.C)/Math.pow(lcup.A*lcup.A+lcup.B*lcup.B, 0.5);
double dl3 = (lcup.A*D3.x+lcup.B*D3.y+lcup.C)/Math.pow(lcup.A*lcup.A+lcup.B*lcup.B, 0.5);
double dl4 = (lcup.A*D4.x+lcup.B*D4.y+lcup.C)/Math.pow(lcup.A*lcup.A+lcup.B*lcup.B, 0.5);
if(dl1<0)
{
cpz[cpznum]=D1;
cpznum++;
}
else if(dl1>0)
{
cpy[cpynum]=D1;
cpynum++;
}
if(dl2<0)
{
cpz[cpznum]=D2;
cpznum++;
}
else if(dl2>0)
{
cpy[cpynum]=D2;
cpynum++;
}
if(dl3<0)
{
cpz[cpznum]=D3;
cpznum++;
}
else if(dl3>0)
{
cpy[cpynum]=D3;
cpynum++;
}
if(dl4<0)
{
cpz[cpznum]=D4;
cpznum++;
}
else if(dl4>0)
{
cpy[cpynum]=D4;
cpynum++;
}
DecimalFormat d=new DecimalFormat();
String style="#.###";
d.applyPattern(style);
if(cpznum==1)
{
Trianges T = new Trianges(cpz[0],lcup.D1,lcup.D2);
double s1 = T.GetMianJi();
double s2 = this.GetMianJi()-s1;
double max = Math.max(s1, s2);
double min = Math.min(s1, s2);
System.out.println(2+" "+Double.parseDouble(d.format(min))+" "+Double.parseDouble(d.format(max)));
}
else if(cpynum==1)
{
Trianges T = new Trianges(cpy[0],lcup.D1,lcup.D2);
double s1 = T.GetMianJi();
double s2 = this.GetMianJi()-s1;
double max = Math.max(s1, s2);
double min = Math.min(s1, s2);
System.out.println(2+" "+Double.parseDouble(d.format(min))+" "+Double.parseDouble(d.format(max)));
}
else if(cpynum==2) //2个四边形
{
SiBianXing q1;
q1 = new SiBianXing(cpy[0],cpy[1],lcup.D1,lcup.D2);
if(q1.IsSiBianXing())
{
double s1 = q1.GetMianJi();
double s2 = this.GetMianJi()-s1;
double max = Math.max(s1, s2);
double min = Math.min(s1, s2);
System.out.println(2+" "+Double.parseDouble(d.format(min))+" "+Double.parseDouble(d.format(max)));
return;
}
q1 = new SiBianXing(cpy[0],cpy[1],lcup.D2,lcup.D1);
if(q1.IsSiBianXing())
{
double s1 = q1.GetMianJi();
double s2 = this.GetMianJi()-s1;
double max = Math.max(s1, s2);
double min = Math.min(s1, s2);
System.out.println(2+" "+Double.parseDouble(d.format(min))+" "+Double.parseDouble(d.format(max)));
return;
}
}
}
}
public void OutOrInSiBianXing(Points p)
{
if((L1.CuoPiontOnLine(p)&&L1.GetPointsToLines(p)==0)||(L2.CuoPiontOnLine(p)&&L2.GetPointsToLines(p)==0)||(L3.CuoPiontOnLine(p)&&L3.GetPointsToLines(p)==0)||(L4.CuoPiontOnLine(p)&&L4.GetPointsToLines(p)==0))
{
System.out.println("on the quadrilateral");
return;
}
Trianges v1,v2,v3,v4;
v1 = new Trianges(L1.D1,L1.D2,p);
v2 = new Trianges(L2.D1,L2.D2,p);
v3 = new Trianges(L3.D1,L3.D2,p);
v4 = new Trianges(L4.D1,L4.D2,p);
if(v1.GetMianJi()+v2.GetMianJi()+v3.GetMianJi()+v4.GetMianJi()==this.GetMianJi())
{
System.out.println("in the quadrilateral");
}
else
{
System.out.println("outof the quadrilateral");
}
}
}
踩坑心得:
1:对于四边形的判断遗漏了“漏斗”的情况,导致测试点没有过全。



所以大家考虑问题的时候要仔细尽量考虑周全在进行解答,不然我就是很好的“例子”最后错哪里都不知道。还是避免不了会犯错的话,熟悉编译器的调试功能会让你水平更上一层楼。
2:直线与四边形的关系分析这个问题至今没有想明白。
3:还有就是正则表达式的正确性了,好的正则表达式就是成功的一半。
2:7-1 点线形系列5-凸五边形的计算-1
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入五个点坐标,判断是否是五边形,判断结果输出true/false。
2:输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"
3:输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
以上3选项中,若输入的点无法构成多边形,则输出"not a polygon"。输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
\2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例1:
选项1,点重合。例如:
1:-1,-1 1,2 -1,1 1,0
输出样例:
在这里给出相应的输出。例如:
wrong number of points
详细信息及样例请查看附件,本题包含附件中的选项1-3的功能:
五边形跟四边形差不多,但是难度进行了一定程度的延申,主要也是要注意判断是否是五边形,凹凸性和分割情况。
这里给出五边形的凹凸性判断
public boolean IsTuPentagon() // 判断错误,改用向量
{
Points PriVector; //第一个
Points LatVector; //第二个
double[] falg = new double[5];
for (int i = 0; i < 5; i++) {
PriVector = new Points((pi[(i + 1) % 5].x - pi[i].x), (pi[(i + 1) % 5].y - pi[i].y));
LatVector = new Points((pi[(i)].x - pi[(i + 4) % 5].x), (pi[(i)].y - pi[(i + 4) % 5].y));
falg[i] = PriVector.x * LatVector.y - PriVector.y * LatVector.x;
}
for (int i = 0; i < 5; i++) { //出现异号则为凹
if (i == 0) {
if (falg[0] * falg[4] < 0)
return false;
} else {
if (falg[i] * falg[i - 1] < 0)
return false;
}
}
return true;
}
class Pentagon {
Points[] pi;
Lines[] Li;
Pentagon() {
}
Pentagon(Points p1, Points p2, Points p3, Points p4, Points p5) //构造五边形(五个点)
{
pi = new Points[5];
Li = new Lines[5];
pi[0] = new Points(p1.x, p1.y);
pi[1] = new Points(p2.x, p2.y);
pi[2] = new Points(p3.x, p3.y);
pi[3] = new Points(p4.x, p4.y);
pi[4] = new Points(p5.x, p5.y);
Li[0] = new Lines(p1, p2);
Li[1] = new Lines(p2, p3);
Li[2] = new Lines(p3, p4);
Li[3] = new Lines(p4, p5);
Li[4] = new Lines(p5, p1);
}
public boolean IsTuPentagon() // 判断错误,改用向量
{
Points PriVector;
Points LatVector;
double[] falg = new double[5];
for (int i = 0; i < 5; i++) {
PriVector = new Points((pi[(i + 1) % 5].x - pi[i].x), (pi[(i + 1) % 5].y - pi[i].y));
LatVector = new Points((pi[(i)].x - pi[(i + 4) % 5].x), (pi[(i)].y - pi[(i + 4) % 5].y));
falg[i] = PriVector.x * LatVector.y - PriVector.y * LatVector.x;
}
for (int i = 0; i < 5; i++) {
if (i == 0) {
if (falg[0] * falg[4] < 0)
return false;
} else {
if (falg[i] * falg[i - 1] < 0)
return false;
}
}
return true;
}
public double GetZhouChang() {
return Li[0].GetLength() + Li[1].GetLength() + Li[2].GetLength() + Li[3].GetLength() + Li[4].GetLength();
}
public double GetMianJi() {
Quadrangle v = new Quadrangle(pi[0], pi[1], pi[2], pi[3]);
Trianges s = new Trianges(pi[0], pi[3], pi[4]);
return v.GetMianJi() + s.GetMianJi();
}
public boolean IsPentagon() {
Lines L12 = new Lines(pi[0], pi[1]);
Lines L23 = new Lines(pi[1], pi[2]);
Lines L34 = new Lines(pi[2], pi[3]);
Lines L45 = new Lines(pi[3], pi[4]);
Lines L51 = new Lines(pi[4], pi[0]);
if ((LineXiangJiaoFeiLingLine(L12, L34, L45)) || (LineXiangJiaoFeiLingLine(L23, L45, L51)) || (LineXiangJiaoFeiLingLine(L34, L51, L12)) || (LineXiangJiaoFeiLingLine(L45, L12, L23)) || (LineXiangJiaoFeiLingLine(L51, L23, L34))) {
// System.out.println(2);
return false;
}
if (LinePingXingLingLine(L12, L23) || LinePingXingLingLine(L23, L34) || LinePingXingLingLine(L34, L45) || LinePingXingLingLine(L45, L51) || LinePingXingLingLine(L51, L12)) {
// System.out.println(3);
return false;
}
return true;
}
public boolean LinePingXingLingLine(Lines l, Lines l1) {
if (l.HaveCupsToLines(l1)) {
return false;
}
return true;
}
public boolean LineXiangJiaoFeiLingLine(Lines L, Lines LN1, Lines LN2) //五边形边与非相邻的边相交(正确返回true)(不相交返回false)
{
Points cupp = L.GetCupsToLines(LN1);
if ((L.CuoPiontOnLine(cupp) && LN1.CuoPiontOnLine(cupp))) {
return true;
}
cupp = L.GetCupsToLines(LN2);
if ((L.CuoPiontOnLine(cupp) && LN2.CuoPiontOnLine(cupp))) {
return true;
}
return false;
}
public void LineWithPentagon(Lines l12) {
int cupnum = 0;
Points cup;
Points[] cupi = new Points[4];
if (Li[0].LineCoincideLine(l12) || Li[1].LineCoincideLine(l12) || Li[2].LineCoincideLine(l12) || Li[3].LineCoincideLine(l12) || Li[4].LineCoincideLine(l12)) {
System.out.println("The line is coincide with one of the lines");
}
if (Li[0].HaveCupsToLines(l12)) {
cup = Li[0].GetCupsToLines(l12);
if (Li[0].CuoPiontOnLine(cup)) {
cupi[cupnum++] = cup;
}
}
if (Li[1].HaveCupsToLines(l12)) {
cup = Li[1].GetCupsToLines(l12);
if (Li[1].CuoPiontOnLine(cup) && (cupnum == 0 || (cupnum == 1 && !cupi[0].PointsEqualPoints(cup)))) {
cupi[cupnum++] = cup;
}
}
if (Li[2].HaveCupsToLines(l12)) {
cup = Li[2].GetCupsToLines(l12);
if (Li[2].CuoPiontOnLine(cup) && (cupnum == 0 || (cupnum == 1 && !cupi[0].PointsEqualPoints(cup)))) {
cupi[cupnum++] = cup;
}
}
if (Li[3].HaveCupsToLines(l12)) {
cup = Li[3].GetCupsToLines(l12);
if (Li[3].CuoPiontOnLine(cup) && (cupnum == 0 || (cupnum == 1 && !cupi[0].PointsEqualPoints(cup)))) {
cupi[cupnum++] = cup;
}
}
if (Li[4].HaveCupsToLines(l12)) {
cup = Li[4].GetCupsToLines(l12);
if (Li[4].CuoPiontOnLine(cup) && (cupnum == 0 || (cupnum == 1 && !cupi[0].PointsEqualPoints(cup)))) {
cupi[cupnum++] = cup;
}
}
if (cupnum != 2) {
System.out.println(cupnum);
} else {
Operate OP = new Operate();
Lines cupl = new Lines(cupi[0], cupi[1]);
double m1=0, m2=0;
int d1 = this.PointCoinDingPoint(cupl.D1), d2 = this.PointCoinDingPoint(cupl.D2);
if (d1 != 6 && d1 != 6) {
Trianges v;
if ((d1 == 0 && d2 == 2) || (d1 == 2 && d2 == 0))
v = new Trianges(cupl.D1, cupl.D2, pi[1]);
else if ((d1 == 1 && d2 == 3) || (d1 == 3 && d2 == 1))
v = new Trianges(cupl.D1, cupl.D2, pi[2]);
else if ((d1 == 2 && d2 == 4) || (d1 == 4 && d2 == 2))
v = new Trianges(cupl.D1, cupl.D2, pi[3]);
else if ((d1 == 3 && d2 == 0) || (d1 == 0 && d2 == 3))
v = new Trianges(cupl.D1, cupl.D2, pi[4]);
else
v = new Trianges(cupl.D1, cupl.D2, pi[0]);
m1 = Math.min(v.GetMianJi(), this.GetMianJi() - v.GetMianJi());
m2 = Math.max(v.GetMianJi(), this.GetMianJi() - v.GetMianJi());
System.out.println(2 + " " + OP.GeShiOutPut(m1) + " " + OP.GeShiOutPut(m2));
}
else {
Points[] plz = new Points[3]; //<0
Points[] ply = new Points[3]; //>0
int znum = 0,ynum = 0;
for(int i=0;i<5;i++) //将点分开,在线的两侧
{
if((cupl.A*pi[i].x+cupl.B*pi[i].y+cupl.C)/Math.pow(cupl.A*cupl.A+cupl.B*cupl.B, 0.5)<0)
{
plz[znum++] = pi[i];
}
if((cupl.A*pi[i].x+cupl.B*pi[i].y+cupl.C)/Math.pow(cupl.A*cupl.A+cupl.B*cupl.B, 0.5)>0)
{
ply[ynum++] = pi[i];
}
}
Trianges v ;
if(znum == 1)
{
v = new Trianges(cupl.D1,cupl.D2,plz[0]);
m1 = v.GetMianJi();
}
else if(ynum == 1)
{
v = new Trianges(cupl.D1,cupl.D2,plz[0]);
m1 = v.GetMianJi();
}
else if(znum == 2)
{
Quadrangle q = new Quadrangle(cupl.D1,cupl.D2,plz[0],plz[1]);
if(q.IsSiBianXing()) {
m1 = q.GetMianJi();
}
else {
q = new Quadrangle(cupl.D1, cupl.D2, plz[1], plz[0]);
m1 = q.GetMianJi();
}
}
else if(ynum == 2){
Quadrangle q = new Quadrangle(cupl.D1,cupl.D2,ply[0],ply[1]);
if(q.IsSiBianXing()) {
m1 = q.GetMianJi();
}
else {
q = new Quadrangle(cupl.D1, cupl.D2, ply[1], ply[0]);
m1 = q.GetMianJi();
}
}
m2 = this.GetMianJi()-m1;
}
}
}
private int PointCoinDingPoint(Points d) {
for (int i = 0; i < 5; i++) {
if (pi[i].PointsEqualPoints(d)) {
return i;
}
}
return 6;
}
}
7-2 点线形系列5-凸五边形的计算-2
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
4:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)。
各种关系的输出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况。
6:输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。输入入错存在冗余点要排除,冗余点的判定方法见选项5。如果点在多边形的某条边上,输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
\2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例:
在这里给出一组输入。例如:
4:0,0 6,0 7,1 8,3 6,6 0,0 6,0 7,1 8,3 6,6
输出样例:
在这里给出相应的输出。例如:
the previous pentagon coincides with the following pentagon
更多样例请查看附件:
[点线形系列5-五边形题目详情.pdf](


踩坑心得:
1:在经过四边形的“毒打”下写五边形的问题解决犯的错误相对更少(因为前面错过了)。
2:懂得熟练进行调试会让问题变得更加简单。
https://images.ptausercontent.com/68388f4f-d3b9-4d60-bb14-f8ebbcec3d0a.pdf)
接下来就是期中测试的题目了,因为难度和题量都不大,所以这里一起说了。
7-1 点与线(类设计)
-
设计一个类表示平面直角坐标系上的点Point,私有属性分别为横坐标x与纵坐标y,数据类型均为实型数,除构造方法以及属性的getter与setter方法外,定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息,格式如下:
(x,y),数值保留两位小数。为简化题目,其中,坐标点的取值范围设定为(0,200]。若输入有误,系统则直接输出Wrong Format -
设计一个类表示平面直角坐标系上的线Line,私有属性除了标识线段两端的点point1、point2外,还有一个字符串类型的color,用于表示该线段的颜色,同样,除构造方法以及属性的getter与setter方法外,定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息,输出格式如下:
The line's color is:颜色值 The line's begin point's Coordinate is: (x1,y1) The line's end point's Coordinate is: (x2,y2) The line's length is:长度值其中,所有数值均保留两位小数,建议可用
String.format("%.2f", data)方法。设计类图如下图所示。
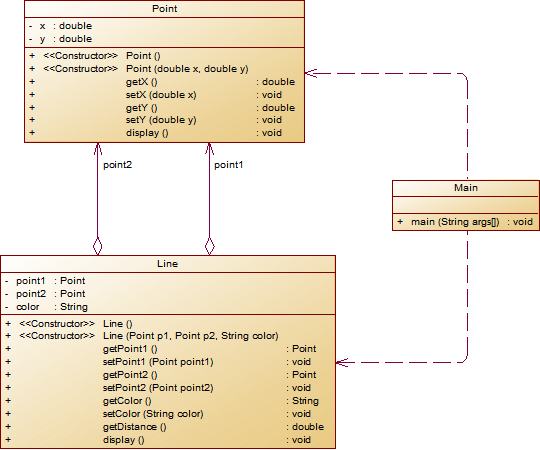
** 题目要求:在主方法中定义一条线段对象,从键盘输入该线段的起点坐标与终点坐标以及颜色,然后调用该线段的display()方法进行输出。**
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red
输出样例1:
在这里给出相应的输出。例如:
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
输入样例2:
在这里给出一组输入。例如:
80.2356
352.12
24.5
100
Black
输出样例2:
在这里给出相应的输出。例如:
Wrong Format
以下是相关代码:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
double x1,x2,y1,y2;
String s;
x1 = in.nextDouble();
y1 = in.nextDouble();
x2 = in.nextDouble();
y2 = in.nextDouble();
s = in.next();
if(InPutIsRight(x1)&&InPutIsRight(y1)&&InPutIsRight(x2)&&InPutIsRight(y2)){
Point point1 = new Point(x1,y1);
Point point2 = new Point(x2,y2);
Line line = new Line(point1,point2,s);
line.display();
}
else{
System.out.println("Wrong Format");
}
}
public static boolean InPutIsRight(double num){
if(num>0&&num<=200)
return true;
return false;
}
}
class Point{
private double x;
private double y;
public Point() {
}
public Point(double x, double y) {
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public double getY() {
return y;
}
public void setX(double x) {
this.x = x;
}
public void setY(double y) {
this.y = y;
}
public void display(){
System.out.println("("+getX()+","+getY()+")");
}
}
class Line{
private Point point1 = new Point();
private Point point2 = new Point();
private String color;
public Line() {
}
public Line(Point point1, Point point2, String color) {
this.point1 = point1;
this.point2 = point2;
this.color = color;
}
public void setPoint1(Point point1) {
this.point1 = point1;
}
public void setPoint2(Point point2) {
this.point2 = point2;
}
public void setColor(String color) {
this.color = color;
}
public Point getPoint1() {
return point1;
}
public Point getPoint2() {
return point2;
}
public String getColor() {
return color;
}
public double getDistance(){
return Math.pow(Math.pow(point2.getX()-point1.getX(),2)+Math.pow(point2.getY()-point1.getY(),2),0.5);
}
public void display(){
System.out.println("The line's color is:"+getColor());
System.out.println("The line's begin point's Coordinate is:\n"+"("+String.format("%.2f", point1.getX())+","+String.format("%.2f",point1.getY() )+")");
System.out.println("The line's end point's Coordinate is:\n"+"("+String.format("%.2f", point2.getX())+","+String.format("%.2f", point2.getY())+")");
System.out.println("The line's length is:"+String.format("%.2f", getDistance()));
}
}
7-2 点线面问题重构(继承与多态)
在“点与线(类设计)”题目基础上,对题目的类设计进行重构,以实现继承与多态的技术性需求。
-
对题目中的点Point类和线Line类进行进一步抽象,定义一个两个类的共同父类Element(抽象类),将display()方法在该方法中进行声明(抽象方法),将Point类和Line类作为该类的子类。
-
再定义一个Element类的子类面Plane,该类只有一个私有属性颜色color,除了构造方法和属性的getter、setter方法外,display()方法用于输出面的颜色,输出格式如下:
The Plane's color is:颜色 -
在主方法内,定义两个Point(线段的起点和终点)对象、一个Line对象和一个Plane对象,依次从键盘输入两个Point对象的起点、终点坐标和颜色值(Line对象和Plane对象颜色相同),然后定义一个Element类的引用,分别使用该引用调用以上四个对象的display()方法,从而实现多态特性。示例代码如下:
element = p1;//起点Point element.display(); element = p2;//终点Point element.display(); element = line;//线段 element.display(); element = plane;//面 element.display();类结构如下图所示。
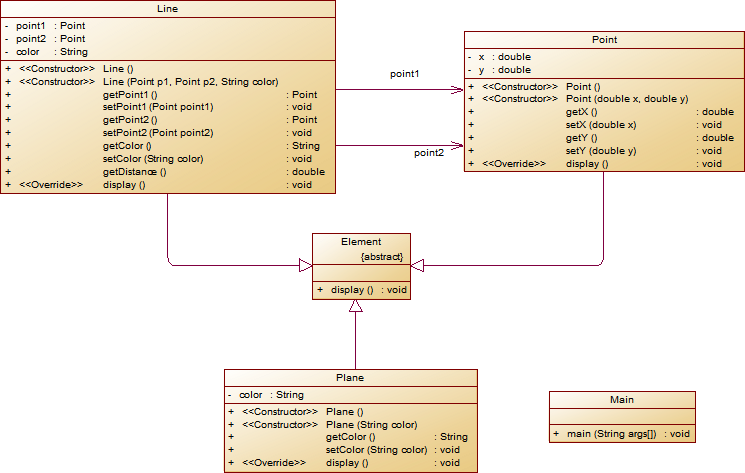
其中,所有数值均保留两位小数,建议可用String.format("%.2f", data)方法。
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
(x1,y1)
(x2,y2)
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
The Plane's color is:颜色值
输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red
输出样例1:
在这里给出相应的输出。例如:
(5.00,9.40)
(12.30,84.00)
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
The Plane's color is:Red
输入样例2:
在这里给出一组输入。例如:
5
9.4
12.3
845
Black
输出样例2:
在这里给出相应的输出。例如:
Wrong Format
这里代码实现上都差不多就不进行展示了
7-3 点线面问题再重构(容器类)
在“点与线(继承与多态)”题目基础上,对题目的类设计进行重构,增加容器类保存点、线、面对象,并对该容器进行相应增、删、遍历操作。
-
在原有类设计的基础上,增加一个GeometryObject容器类,其属性为
ArrayList<Element>类型的对象(若不了解泛型,可以不使用<Element>) -
增加该类的
add()方法及remove(int index)方法,其功能分别为向容器中增加对象及删除第index - 1(ArrayList中index>=0)个对象 -
在主方法中,用户循环输入要进行的操作(choice∈[0,4]),其含义如下:
- 1:向容器中增加Point对象
- 2:向容器中增加Line对象
- 3:向容器中增加Plane对象
- 4:删除容器中第index - 1个数据,若index数据非法,则无视此操作
- 0:输入结束
示例代码如下:
choice = input.nextInt(); while(choice != 0) { switch(choice) { case 1://insert Point object into list ... break; case 2://insert Line object into list ... break; case 3://insert Plane object into list ... break; case 4://delete index - 1 object from list int index = input.nextInt(); ... } choice = input.nextInt(); }输入结束后,按容器中的对象顺序分别调用每个对象的
display()方法进行输出。
类图如下所示:
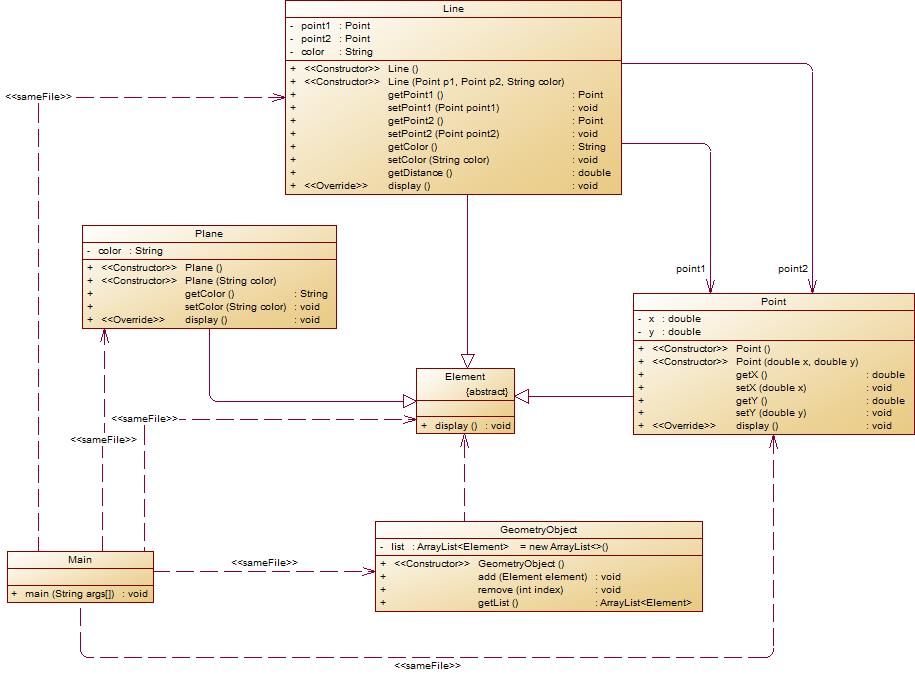
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
switch(choice) {
case 1://insert Point object into list
输入“点”对象的x,y值
break;
case 2://insert Line object into list
输入“线”对象两个端点的x,y值
break;
case 3://insert Plane object into list
输入“面”对象的颜色值
break;
case 4://delete index - 1 object from list
输入要删除的对象位置(从1开始)
...
}
输出格式:
- Point、Line、Plane的输出参考题目2
- 删除对象时,若输入的index超出合法范围,程序自动忽略该操作
输入样例:
在这里给出一组输入。例如:
1
3.4
5.6
2
4.4
8.0
0.98
23.888
Red
3
Black
1
9.8
7.5
3
Green
4
3
0
输出样例:
在这里给出相应的输出。例如:
(3.40,5.60)
The line's color is:Red
The line's begin point's Coordinate is:
(4.40,8.00)
The line's end point's Coordinate is:
(0.98,23.89)
The line's length is:16.25
(9.80,7.50)
The Plane's color is:Green



 浙公网安备 33010602011771号
浙公网安备 33010602011771号