集成学习入门及代码实现
bagging原理
bagging的思路是训练k个独立的基学习器,对于每个基学习器的结果进行结合(加权或者多数投票)来获得一个强学习器。
boostrap
boost最早用于经济学,为了研究大样本中的特征值,通过有放回的多次采样研究样本的特征。
- 在原有的样本中通过重抽样抽取一定数量(比如100)的新样本,重抽样(Re-sample)的意思就是有放回的抽取,即一个数据有可以被重复抽取超过一次。
- 基于产生的新样本,计算我们需要估计的统计量。
- 重复上述步骤n次(一般是n>1000次)。
- 最后,我们可以计算被估计量的均值和方差
其中,均值为n次采样的平均值的均值,方差为n次采样方差/样本数-1
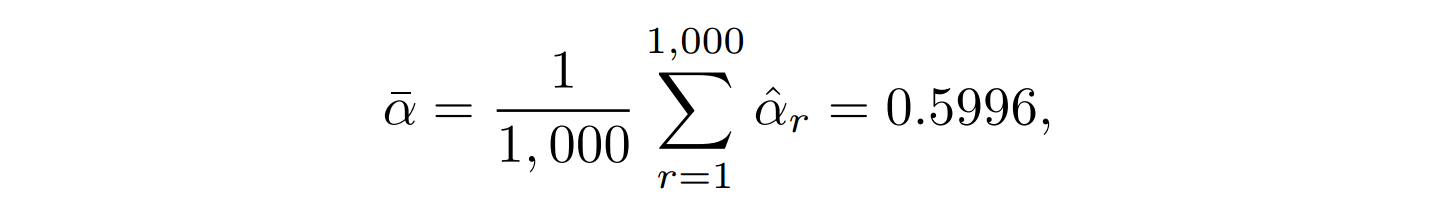
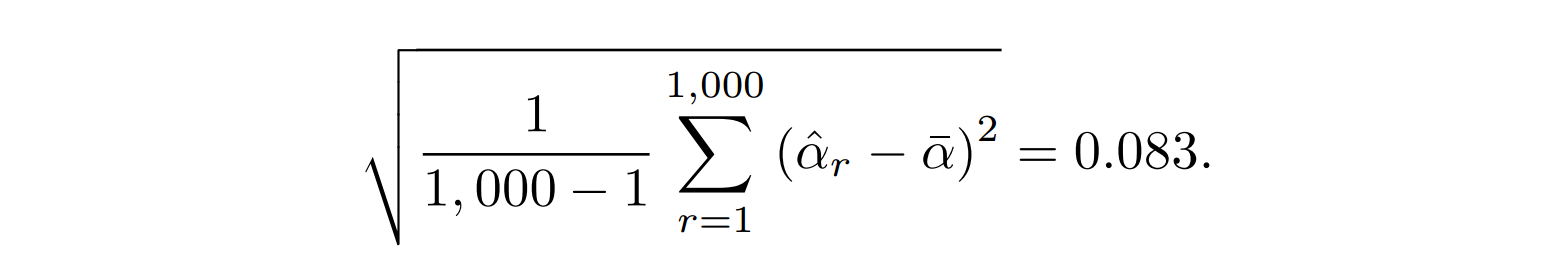
类似于概统中的样本分布估计总体
在此bagging使用了boostrap的思想,从m个样本的训练集中有放回地抽取m次,获得第一个样本集,用于训练第一个基学习器,以此类推可获得k个样本集供基学习器训练。由于训练数据不同,我们获得的基学习器会有很大的差异。同时保证了数据尽可能被使用到。
由于使用了boostrap进行训练集的抽取,由于其抽泣方法的特性,会有约0.368的样本未被抽到,此部分样本称为包外样本(记作oobs),可用作测试集,此部分的测试结果称为“包外估计”,为真实误差的无偏估计。
obbs估计等价于k折交叉验证,使用obbs作为测试集能大幅减少计算。
基分类器选取
bagging要求基分类器对样本分布敏感,常用的基分类器为决策树、神经网络。KNN、线性分类器由于过于“稳定”不适合作为基分类器。
- 树的节点分裂随机选择特征子集带来随机性,设定层数来控制泛化;
- 神经网络通过调整神经元数量、连接方式、网络层数、初始权值引入随机性;
基分类器聚合
bagging的另一个重要步骤是模型聚合,我们通常使用比较简单的方法来聚合多个模型,对于分类问题我们采用投票的方式,将出现最多的一个作为分类结果,对于回归问题取m个的平均值。
RandomForest
样本集N,共N个样本;特征集M,共M个特征
(1)样本集N中以boostrap方法抽取k个训练集,每个训练集样本个数为n(第一个随机,随机有放回抽取),且分类误差取决于:
- 每棵树的分类能力:单棵树分类能力越强,分类误差越小
- 树之间的相关性:树之间的相关性越小,分类误差越小
(2)对每个训练集,抽取M个特征中的m个特征(随机无放回抽取):
- M较大时: m=\(log_2\)M或\(m=log_2M+1\);
- M较小时,在M中取L个特征(L<k),用[-1, +1]上的均匀分布来构建权重对L个特征进行线性组合,构成k个特征;
- m越小,相关性越小、分类能力越差;
- 是随机森林唯一的超参(在不考虑树本身的超参前提下),可以使用obb error(out of bag error)进行选择
(3)对某n个样本的训练集,m个特征的特征集进行决策树训练
- 只训练二叉树:减少计算量;方便模型构建
- 无需剪枝:满足差异性;减少计算量
m = n时,RF等价于CART树
m越小,模型方差减小,偏差增大,趋近欠拟合;m越大,模型方差增大,偏差减小,趋近过拟合
bagging方法的代码实现——用于鸢尾花数据集
导入相关的库
from sklearn import neighbors
from sklearn import datasets
from sklearn.ensemble import BaggingClassifier
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
数据加载
加载鸢尾花数据集进行demo实现
iris = datasets.load_iris()
x_data = pd.DataFrame(iris.data, columns=iris.feature_names)
y_data = iris.target # 标签
x_train,x_test,y_train,y_test, = train_test_split(x_data,y_data)
为了方便可视化,我们选取两列
x_data = x_data[['sepal width (cm)','petal length (cm)']]
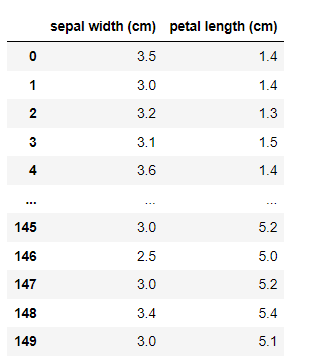
分割数据集
X_train,X_test,y_train,y_test = train_test_split(x_data,y_data,
test_size = 1/3,random_state = 0)
我们利用KNN进行bagging实验
knn = neighbors.KNeighborsClassifier()
knn.fit(X_train,y_train)
plot(knn)
plt.scatter(x_data.iloc[:,0],x_data.iloc[:,1],c = y_data)
plt.show()
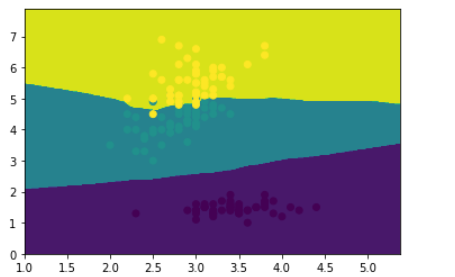
此时的得分为0.94
使用集成学习 参数(一个模型,有返回的抽样一百次) ,就是说进行一百次的knn分类器去分类,然后进行投票最高的那个模型
bagging_knn = BaggingClassifier(knn,n_estimators=60)
# 输入数据建立模型
bagging_knn.fit(X_train,y_train)
plot(bagging_knn)
# 样本散点图
plt.scatter(x_data.iloc[:,0],x_data.iloc[:,1],c = y_data)
plt.show()
bagging_knn.score(X_test,y_test)
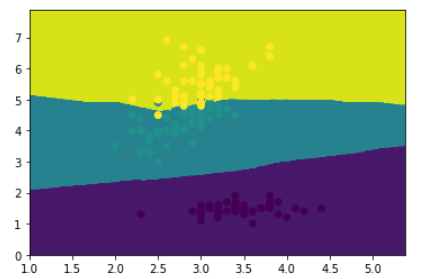
将KNN模型bagging的分类结果
得到结果为0.96
绘图函数放在这里,这种画法可以较好地可视化分类问题。
def plot(model):
# 获取数据所在的范围
x_min,x_max = x_data.iloc[:,0].min() - 1,x_data.iloc[:,0].max()+1
y_min,y_max = x_data.iloc[:,1].min() - 1,x_data.iloc[:,1].max()+1
#生成网格矩阵
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02),
np.arange(y_min,y_max,0.02))
z = model.predict(np.c_[xx.ravel(),yy.ravel()]) # ravel与flatten类似,多维数据转一维.flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape)
# 登高线图
cs = plt.contourf(xx,yy,z)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号