自然语言处理实战---基于HMM算法实现命名实体识别

是《自然语言处理》课程的小作业之一，内容是基于隐马尔科夫模型进行命名实体识别任务。

引言

本文要求基于HMM模型进行命名实体识别任务，数据集中共有十个标签类别，分别为: 地址（address），书名（book），公司（company），游戏 （game）政府（government）， 电影（movie），姓名（name），组织机构（organization），职位（position），景点（scene）。任务要求利用隐马尔可夫标注命名实体。实例如下：

隐马尔可夫模型介绍

隐马尔可夫模型是比较经典的机器学习模型，它在语言识别，自然语言处理，模式识别等领域都得到广泛的应用。其结构图如下所示：

上图中\(Y_i\)为隐藏状态序列，其可取的隐藏状态空间定义如下式所示。其中，\(n\)为所有可取的隐藏状态数。

\[Q = q_1,q_2,...,q_n \]

而\(X_i\)为观测状态序列，其观测状态空间定义如下式所示。其中，\(m\)为所有可能的观测状态数。

\[V = v_1,v_2,...,v_m \]

同时，隐马尔可夫含有两个假设：
• 齐次马尔可夫链假设：假设当前的隐藏状态 仅依赖于前一个时刻的隐藏状态 ，而与其它时刻的隐藏状态无关。如上图中的箭头所示。
• 观测独立性假设： 即任意时刻的观察状态 只仅仅依赖于当前时刻的隐藏状态 。如上图中的箭头所示。

利用隐马尔可夫模型实现命名实体识别

基于隐马尔可夫的模型可以将命名实体识别问题转化为序列标注问题——定义一个实体开始的字标记为B；实体中间的字标记为I，不属于实体的字标记为O，在本人的模型中，为了使得实体的结束位置更加精确，我在实体的末尾多定义了一种状态S，以便于较好地切分实体单元。

使用隐马尔可夫模型进行实体识别，就是给定一个句子，然后通过隐马尔可夫模型求出该句子对应的标注，然后基于标注提取命名实体。
在隐马尔可夫模型中，标注为隐藏状态序列\(Y_i\) ，而句子为观测序列\(X_i\) 。要求出隐藏状态序列\(Y_i\) ，就是在给定观测序列\(X_i\)的条件下，使其概率达到最大。即：

\[(Y_1,Y_2,...,Y_t) = \arg\max(Y_1,Y_2,...,Y_t|X_1,X_2,...,X_t) \]

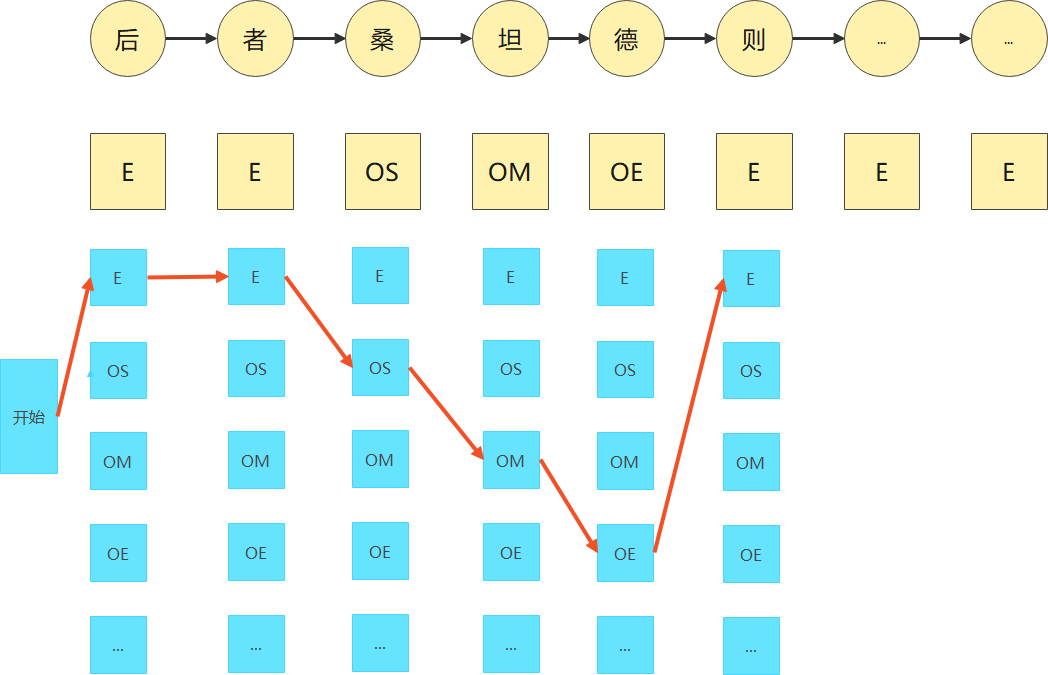
实际就构成了一个最优路径问题，目标是在观测序列已知时，找到概率最大的隐藏状态

利用维特比算法实现序列标注

维特比算法使用了动态规划的思想：如果最优路径在时刻\(T_t\)通过节点\(T_t^i\)。那么这一路径从节点\(T_0\)到节点\(T_t^i\)之间的路径一定是最优的。

列出状态转移方程

\[V_{1,k}=P(y_1|k)\cdot \pi_k \]

\[V_{t,k}=P(y_t|k) \cdot max_{x \in S}(a_{x,k}\cdot V_{t-1,x}) \]

其中，\(V_{i,k}\)指的是时刻t下出现隐藏状态k的概率
取\(V_{t,k}\)中取值最大的数，得到一条最大的路径。

代码实现

这里是代码实现的思路

训练数据的标注

数据分为10个标签类别，分别为: 地址（address），书名（book），电影（movie），姓名（name），组织（organization），公司（company），游戏（game），政府机构（goverment），职位（position），景点（scene）。

为了便于处理，我们采用了开头-中间-结尾的标签标注规则，对于每一个标签类型设置其缩写如下所示：

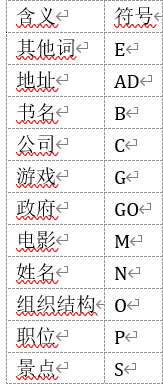
其中缩写+S代表命名实体开头，缩写+M表示中间词，缩写+E代表符号结尾。
根据此规则对训练进行标注，代表着每一个字的隐含状态，便于之后进行训练。
一共有31种标注标签。

模型的训练

隐马尔可夫的训练过程就是基于训练集样本统计出各种状态的占比，得到其初始状态矩阵\(\pi\)和转移状态矩阵\(A\)，以及发射矩阵\(B\)，实质上是一个用频率估计概率的过程 。我们定义init_mat，储存初始状态矩阵 \(\pi\)，transform_mat储存状态转移矩阵\(A\)，singleword_mat储存状态发射矩阵\(B\),训练中的结果如下所示：
初始状态矩阵
初始状态矩阵的含义是初始状态出现某一状态的概率：

状态转移矩阵A
状态转移矩阵的横轴和纵轴都是隐含的状态，根据我们先前设置的状态，该状态转移矩阵为31×31的矩阵。

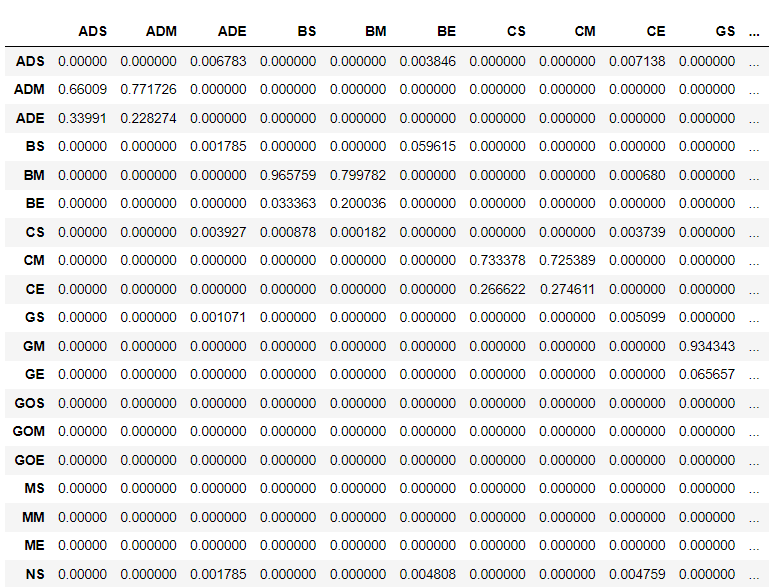
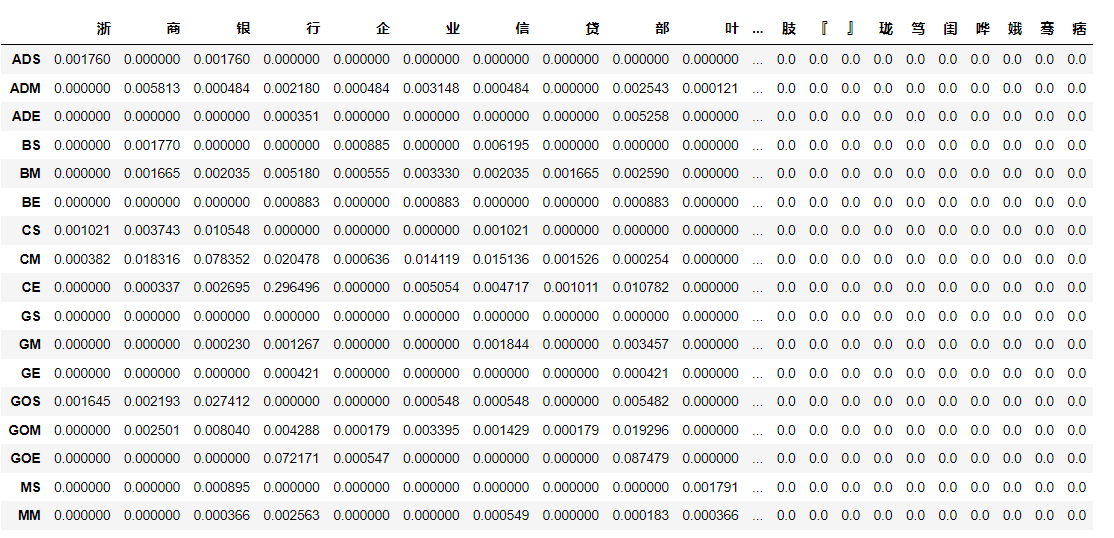
发射矩阵B
发射矩阵衡量的是一个隐藏状态下出现每个字符的概率，在本实验中，是一个31×3671的矩阵。

基于维特比算法进行计算

定义to_seq函数基于发射矩阵，初始状态矩阵和状态转移矩阵，对句子进行标注，得出其结果，其数学推导在第二章中已经论述过了。下面展示一下标注结果：

利用标注结果进行划分

定义cut函数，作为识别命名实体的函数。
调用函数cut(sentence, to_seq(sentence, init_mat, transform_mat, singleword_mat))，得到命名实体的识别结果如下：

编码的转化

本文定义的标注类型和实验要求的标注类型有一定的出入，定义transform函数现将编码标准化，将编码转化为B-缩写和I-缩写形式。
经过转化的编码可以利用seqeval模块进行评估。

结果分析

使用seq-eval函数进行模型结果的评估。

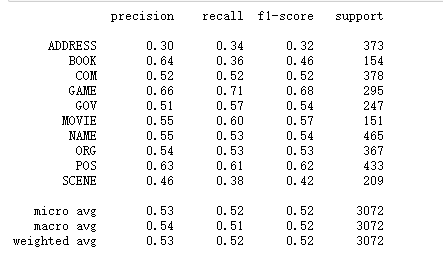
对于隐藏状态数的选择

对于隐含状态的数目的选择，有两种常规的思路，正如我在前面所说的，既可以将命名实体的开头和其余部分标为两个状态，此时共有21种隐含状态，也可以将开头，中间，结尾三个部位分别设为三个状态，此时共有31种隐含状态。
这两种设置方式对应了不同的结果：

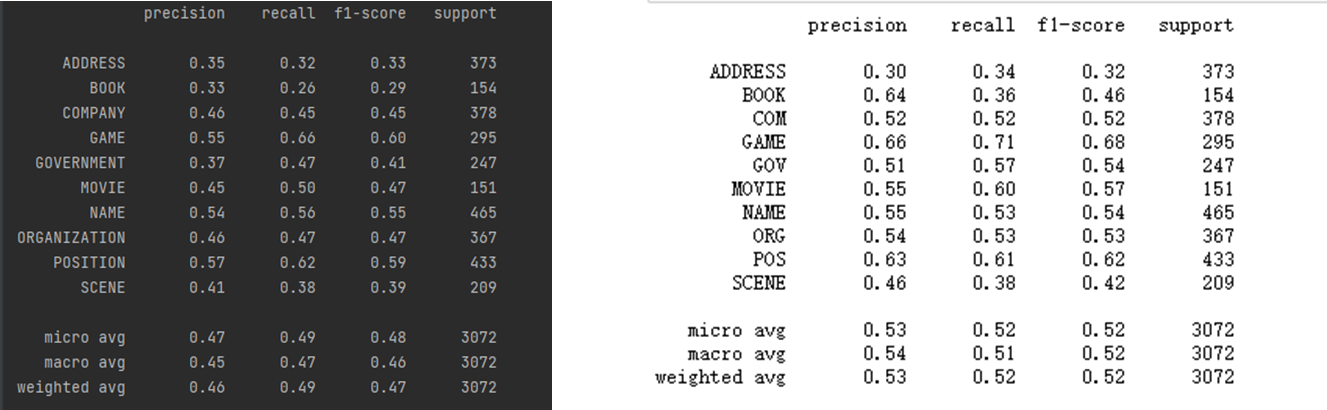
如上图，左边是其他同学使用21种状态的标注结果，右边是我使用31种状态的结果，明显31种隐含状态的标注方法更优。

模型局限性

对于实现的算法，有两大局限性：
效率低：进行一次训练需要十几分钟的时间，效率太低
对生字敏感：由于发射矩阵的特性，导致模型不能识别没有出现过的生字。
解决方案：对于第一种情况，需要我们优化代码，以达到更高的效率，对于第二种方法，目前可行的解决方案是尽可能扩展训练数据集，以达到更全面的识别效果。

对于未出现字的处理我采用了一种偷懒的方法：处理未出现字时会出错，我就直接用try...except捕捉这个错误，当作处理失败，感觉会有更好的解决方法

代码链接

https://gitee.com/xiaoyun-blog/GRE-base-on-HMM/tree/master/