统计学习方法 3 K近邻

原理

K近邻，对于一个点，求和它数量最近的K的元素的类别，以此推断它的类别

1. K近邻思想：物以类聚

2. K近邻没有显式的训练过程

3. 距离度量：

   （1）欧式距离：两点之间直线

   （2）曼哈顿距离：城市街区距离

   （3）切比雪夫距离：棋盘距离

K值选择

选择较小的k值

用较小的邻域进行预测。预测结果对邻 近的实例点非常敏感。如果邻近的实例点恰好是噪声，预测就会出错。

选择较大的k值

用较大的邻域进行预测。对于输入实例 较远的（已经不太相似）的样本点也会对预测起作用，使预测发生错误。

在应用中，一般先取一个较小的K值，再通过交叉验证 法来选取最有的K值

多数表决算法

按多数的类型来决定应分到的类别

也可以定义一个损失函数，其含义为一个以待测点为中心的圆中，分类错误的个数

损失函数为

\[\frac{1}{k}\sum_{x_i \in N_k(x)}I(y_i \neq c_j) \]

以下图为例：

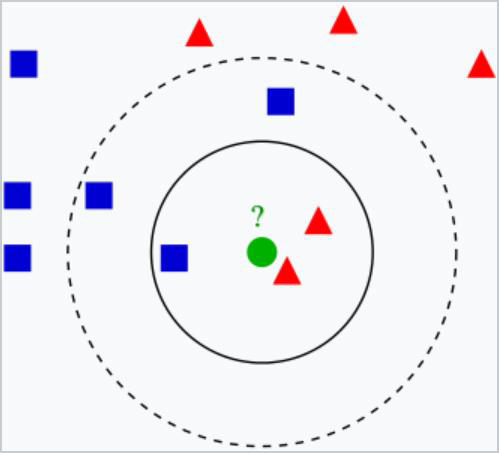
此时实心圆内都判断为红色的损失值（0+0+1）*1/3 = 1/3

实心圆内都判断为蓝色的损失值（0+1+1）*2/3 = 2/3

KD树

KD树通过分割平面来保证最高效率地查找（从近到远）

1. Kd树采用了特殊的结构存储训练数据。
2. Kd树可以减少计算距离的次数。
3. 但当空间维数接近训练实例数时，它的效率会迅速下降。