统计学习方法 2 感知机

模型内容

求\(f(x)\)

\[f(x)=sign(\omega \cdot x + b ) \]

其中，signx在大于零的时候取值为1，否则取值为0

𝒘 · 𝒙 + 𝒃是一个n维空间中的超平面S，其中w是超平面的法向量，b是超平面的截距，这个 超平面将特征空间划分成两部分，位于两部分的点分别被分为正负两类，所以，超平面S称 为分离超平面。

w是超平面的法向量

b是超平面的截距

特征空间也就是整个n维空间，样本的每个属性都叫一个特征，特征空间的意思是在这个空 间中可以找到样本所有的属性组合

模型的范围

适用于线性可分的数据集

函数间隔和几何间隔

函数间隔

\[|\omega \cdot x_0 + b| \]

几何间距

\[\frac{1}{||\omega||}|w\cdot x_0 + b| \]

感知机的损失函数

\(-y_i(\omega \cdot x_i+b)>0\)

说明此时\(w \cdot x_i+b\)和预测标签异号

\(-\frac{1}{||\omega||}y_i(\omega \cdot x_i+b)0\)

一次，所有误分类点到超平面S的总距离为

\(-\frac{1}{||\omega||}\sum_{x_i\isin M}y_i(\omega \cdot x_i+b)\)

由于感知机是默认数据集线性可分的，所以此时衡量距离对结果无影响，此时只要使误分类的数量最少，就会自动最后到0

\(L(\omega,b)=-\sum_{x_i \isin M}y_i(\omega \cdot x_i+b)\)

此时的策略称为误分类驱动

学习过程

1. 任选取超平面 \(𝑤_0\),\(𝑏_0\)

2. 采用梯度下降法极小化目标函数

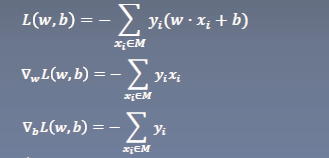
3. 更新\(\omega\),\(b\)
   \[\omega \leftarrow \omega + \eta y_ix_i \]

\[b \leftarrow b + \eta y_i \]

感知机的对偶形式

对偶实例可以减少运算量