统计学习方法 1 绪论
统计学习的三要素
模型
输出的模型有两类,决策函数或条件概率分布
决策函数,表示属于哪一个类别
条件概率分布,表示分布空间
策略
损失函数

求极值的策略
经验风险最小化
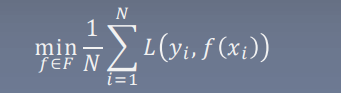
结构风险最小化
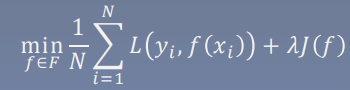
添加正则项以防止过拟合,正则项可用于约束模型参数大小或者值的个数,调整模型结构,减少复杂度
算法
挑选一个合适的算法, 使得可以求解最优模型
训练集,验证集,测试集
数据集 随机划分为 以下3部 分,
- 训练集:模型的训练 train
- 测试集:模型的选择 dev
- 验证集:模型的评估 test
| 轮次 | train | dev |
|---|---|---|
| 0 | 30 | 25 |
| 1 | 50 | 51 |
| 2 | 70 | 75 |
| 3 | 90 | 60 |
| 4 | 95 | 43 |
由验证集知,训练三次之后出现过拟合的趋势,所以选择第三次作为结果放入验证集中评估
泛化能力
泛化误差上界
对于二分类问题,当假设空间是 有限个函数的集合𝐹 = 𝑓1, 𝑓2, ⋯ , 𝑓𝑑 时,对任意一个函 数𝑓 ∈ 𝐹,至少以概率1 − 𝛿,以 下不等式成立:
其中\(R(f)\)是泛化误差(期望风险),含义为\(E[L(Y,f(x))]\),为损失函数的期望
\(\hat{R}(f)\)是经验误差(经验风险),指测试集中误差的平均值
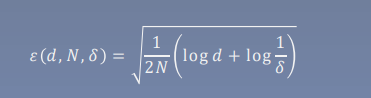
推导很麻烦,关键是记住结论:
-
经验风险越小,期望风险越小
-
数据集越大,经验风险越小(观察\(\epsilon\)项)
生成式模型与判别式模型
生成方法
模型表示了给定输入X后产生输出Y的生成关系,包括贝叶斯和马尔可夫模型
判别方法
直接学习决策函数或概率分布密度
\(f(X)\)或\(P(y|x)\)
异同
对于生成式模型和判别式模型,有一个比喻,对于一个人的名字,生成式模型是生成其父母直接问其父母,判别式是判断他叫不同名字的概率
分类问题
-
TP—将正类预测为正类数;
-
FN—将正类预测为负类数;
-
FP—将负类预测为正类数;
-
TN—将负类预测为负类数。
T\F表示原本为正/负类
P\N表示预测的结果是正/负类
精确率: 预测为正类的样本中有多少被分对了
召回率:在实际正类中,有多少正类被模型发现了
F1值:
极大似然估计
当一系列事实给定后,我们可以通过已经得知的事 情发生情况去反推隐含的参数,使得在使用这些参 数的情况下,事情按事实发生的概率最大
对于\(p(X|\theta)\)如果\(\theta\)确定,\(X\)不确定,为概率函数,反之,为似然函数
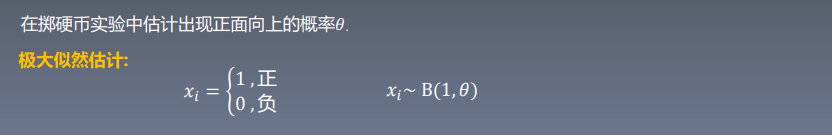
若要使参数成立,则应使参数产生样本结果的概率最高,此时X(i)为已知量
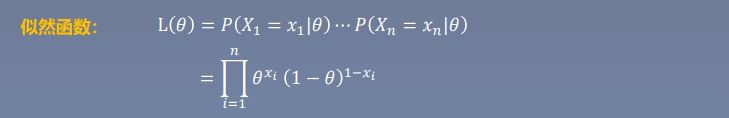



 浙公网安备 33010602011771号
浙公网安备 33010602011771号