# 社会计算《网络、群体与市场》 笔记 9 小世界现象

主要内容

基本实验

两点启示

• “小世界”现象
• “自我寻的”现象

体现小世界现象的模型

体现自我寻的现象的模型

送信实验

Stanley Milgram做了一个实验：

几百名“初始者”，要求每人尝试通过转发让一个指定的人收到一封信；

向每个初始者提供了目标收信人的姓名、地址、职业等个人信息；

规定：参与者只能将信件转发给能直呼其名的熟人，并请他继续转发。因此，如果一个参与者不认识目标收信人，则他不能直接将信寄给他；

结果，约三分之一的信件经过平均六次转发到达了目标

社会网络中包含丰富的短路径

通过“有意识的转发”能够“自动地”找到这些短路径

形成社会网络的两种基本力量

同质性（选择，社会影响），三元闭包

• 家庭成员，邻里关系，同学，同事
• 对应社会网络中的大量的“三角形”
• 体现某种“亲近”（例如地理范围的）

弱联系

• 偶然的联系，认识的“远程”朋友
• 对其所在的圈子并不一定熟悉

Watts-Strogatz模型

存在许多“三角形”和少数随机的“远程边”

小世界网络指聚类系数较大且平均路径长度较小的网络Watts-Strogatz(W-S) 模型

W-S模型的构建: (1)从一个有N个节点的一维规则圆环开始，每一个点与它的r个最近邻居连结。(2)以概率P按顺时针方向对规则圆环中每一条边进行重新连结。重连生成k条边。在重连过程中，不能进行自我连结和重复连结。

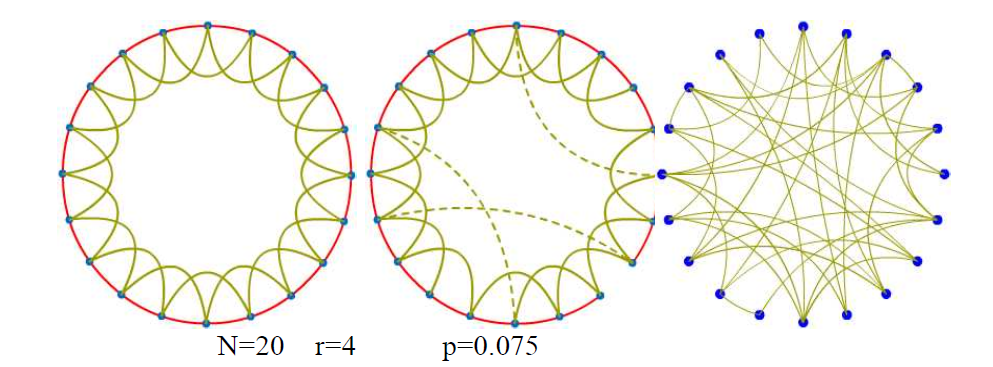
体现了同质连接和弱关系连接的概念（利用r和k控制相关的强度），于是可以看成是现实社会网络的一个合理近似

Watts-Strogatz证明了：在这样的网络中，任意两点之间存在短路径的概率很高

• 基本思路：弱连接的随机性使其形成闭包的概率很小

只要在基础网络结构上存在很少的全局随机性，就可以看到小世界现象

但是这个模型存在的一定的局限性：对于路径的寻找其实是低效的，需要一种既反映任何节点对之间短路径的存在性，也反映这种转发方式达到目的的可能性

扩展的Watts-Strogatz网络模型

同质性局部连接相同：每个节点与在r个网格步内的节点都有直接的边

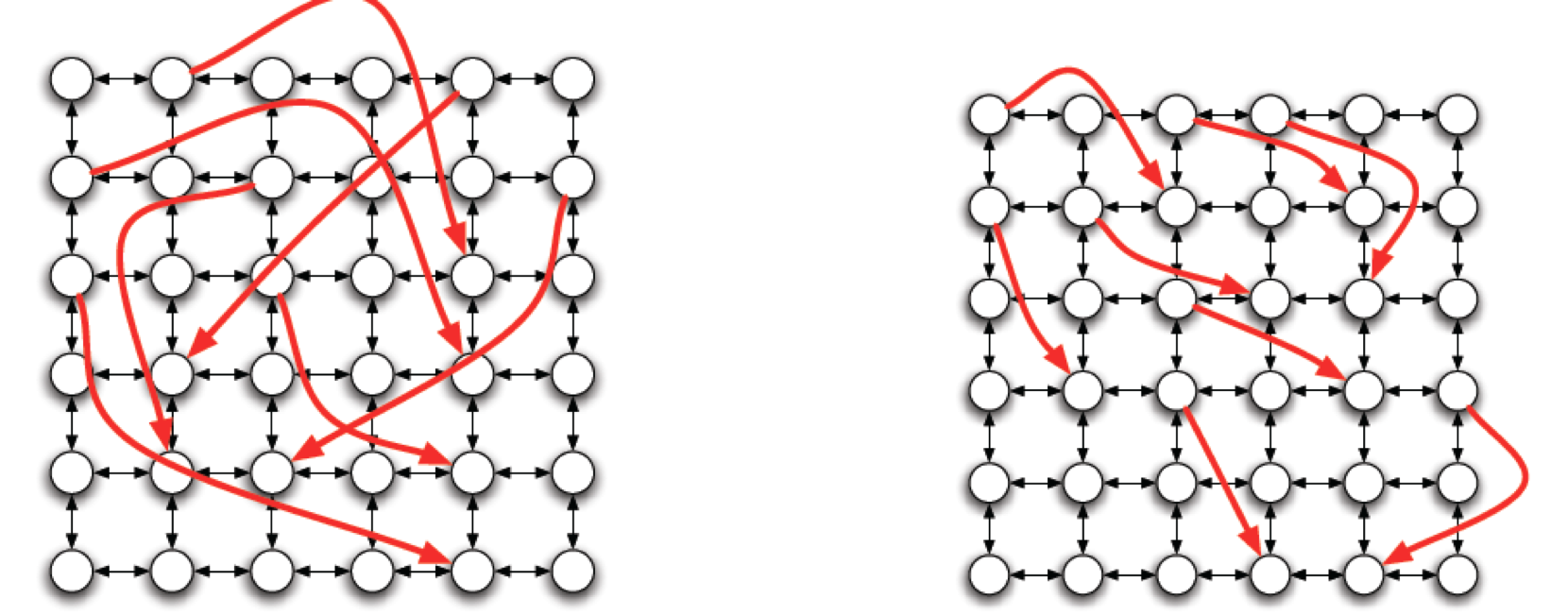
• 对随机远程弱连接加以一定的控制：让两个节点之间连接的概率与它们的网格距离的幂次成反比关系（即随距离增加而衰减）
• 记\(d(v,w)\) 为v到w的距离（网格步数），则产生一条从v到w的随机边的概率与\(d(v,w)^{-q}\) 成正比。

当q=2时，分散搜索达到最佳效果

原因：

节点数与\(d^{2}\) 成正比（均匀分布，节点数与面积成比例），随机连接到其中一个节点的概率与\(d^{-2}\) 成比例

Watts-Strogatz-Kleinbeig网络模型试图反映的社会网络特征

• 由某种“亲近”（相似性）形成的近距离边

• 随机的远距离弱联系边

• 远程相邻节点的数量在同距离节点数中的占比随距离的
  平方减少

Adamic和Adar以惠普实验室人员的email数据为对象进行的分析表明，该性质体现明显：社会距离为d的员工之间产生连接的概率与d-3/4成比例

社团（social foci，社交聚点）与距离

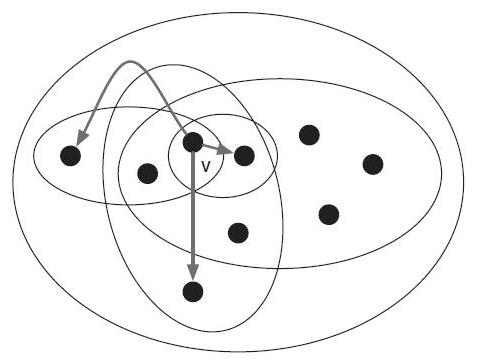
一个人可能参加多种社团（组织机构，兴趣爱好群体等），社团是两人建立关系的一个基础（社团闭包）

可以想象，两人的亲近程度（“距离”）与社团的规模有关，越小越近

定义“社会距离”：两人同属最小社团的规模

配套习题

20.1

在基本的“六度分隔”问题中，有人问是否世界上大多数的人通过社会网络中一条最多有六个边的路径彼此连接，其中连接任何两个人的边基于能够直呼其名的关系。

现在，我们考虑这个问题的一个变化形式。假设我们考虑整个世界的人口，并假设每个人到其 10 个最亲密的朋友分别创建一条有向边（除此之外不再与其他好朋友建立连接）。在这个基于“最亲密朋友”的社会网络，是否可能有一条最多六个边的路径连接世界上的每一对人？请解释

答：

基于“最亲密朋友”的社会网络中，不可能有一条最多 6 个边的路径连接世界上的每一个人。 因为“最亲密朋友”的联系属于强关系，这一网络里边的边全部是强关系，而小世界现象产 生需要依靠远距离的弱关系存在，因此不存在这样的路径。

20.3

假设你正在和一个研究小组研究社会交际网络，特别关注在这类网络中人们之间的距离，探索小世界现象更广泛的影响。

该研究小组目前正在与一个大型移动电话公司协商一项协议，了解他们 “谁给谁打电话”的快照。具体而言，根据严格的保密协议，电话公司答应将提供一个图表，其中每个节点代表一个客户，每条边表示固定的一年间一对彼此通话的人。（每条边附加说明呼叫的次数和时间。每个节点并不提供个人的其他信息。）

最近，电话公司提出他们将只提供那些一年中平均每周至少通话一次的边，而不是所有的边。（也就是说，所有节点都包含，但只有那些通话至少 52 次的边。）电话公司知道这并不是完整的网络，但他们坚持提供更少的数据，他们认为这已经是一个很好的逼近完整的网络。

尽管你的研究小组反对，但电话公司依然不愿意改变立场，除非你的团队能确定具体的研究结果，证明这种减少的数据集很可能产生误导。研究小组负责人要求你准备一个简短的论据回应电话公司，确定一些具体方法说明减少的数据集可能会产生误导性的结论。请简述你的论据。

答：

人群中存在着小世界现象，即局部同质性连接上散落着少量随机弱关系。当只提供平均每周至少通话一次的边时，有可能导致少量随机弱关系消失（可以假设弱关系的人之间并不经常联系）。这种减少的数据集事实上剔除了几乎所有的“弱关系”的边，这样整个网络只有“三元闭包”这一类较紧密的关系。在研究中，就极大的增加人与人的距离，产生了较大的误差。
可以通过对得到的数据集建图，来判断是否失真：当弱关系消失时，由此生成的网络会产生误导，因为此时网络中，仅含局部同质性连接。