# 社会计算《网络、群体与市场》 笔记 5 博弈论基础
主要内容
博弈论的基本概念
典型博弈的类型
博弈模型的建立以及实际问题的解决
博弈的基本概念
假设在截止前一天,有两件事情要做
- 考试
- 如果复习,则可以在考试中得到92分,没复习,则只有80分
- 报告需要和拍档一起准备
- 若两人都准备,则两人都是100
- 只有一人,则每人都是92
- 如果两人都没准备,则每人都是84
该如何选择?
如果两人都准备报告,则平均成绩为\(\frac{80+100}{2}=90\)
如果都准备考试,则平均成绩为\(\frac{92+84}{2}=88\)
如果一方复习考试,另一方准备报告的话:
- 准备报告的平均分\(\frac{80+92}{2}=86\)分
- 复习的一方有\(\frac{92+92}{2}=92\)分
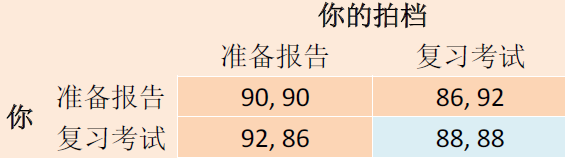
可以据此列出收益矩阵:
| 准备报告 | 复习考试 | |
|---|---|---|
| 准备报告 | 90,90 | 86,92 |
| 复习考试 | 92,86 | 88,88 |
第一个数字表示第一个人(斜体表示的列)的收益,第二个数字表示第二个人(加粗的行)的收益
博弈的基本要素
博弈具有三大要素
- 参与者
- 策略集:每个参与者都有一组关于如何行为的备选项
- 收益(回报):每个策略行为的选择都会使参与人得到一个收益
- 收益结果绝大多数受互动中他人策略选择的影响
- 同一种策略不同参与人的收益可能不同
收益的记号:P1(S,T),P2(S,T)
| 字母 | 含义 |
|---|---|
| P | 受益 |
| S | 第一个人的策略选择 |
| T | 第二个人的策略选择 |
博弈行为的基本假设
- 每个参与人对博弈结构(收益矩阵)有充分的了解
- 参与人都是理性的
- 追求自己的收益最大化
- 知道其他参与人也是如此
- 独立决策,不商量
严格占优策略
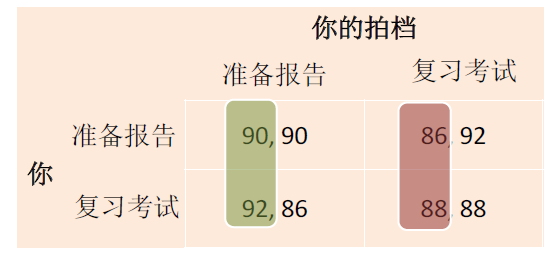
严格占优策略是参与人的最优策略。
如果参与人i的一个纯策略si与其纯策略集Si中所有其他纯策略相比总是最优的,那么si是严格占优策略。不管别人选择了什么策略,严格占优策略总是参与人的最优策略。寻找严格占优策略时应从一个参与人的角度进行考虑,不需要正确预测其他人的行动。
如果一个人有严格占优策略,那么他的其他策略都是严格劣策略,所以参与人一定会选择其严格占优策略。(根据理性原则)
收益决定选择
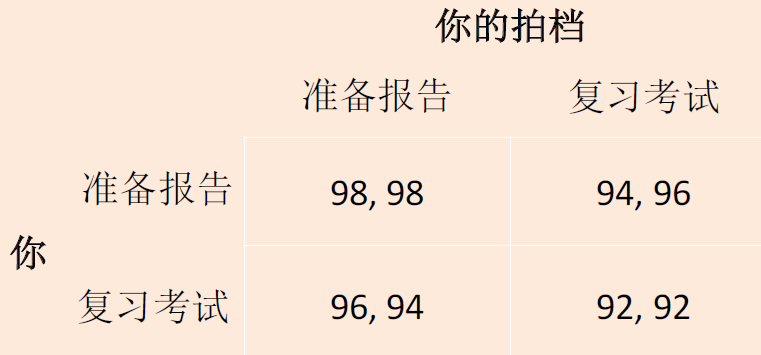
如果降低考试的难度,如图所示,此时的严格占优策略发生了变化,变为准备报告,此时我们可以发现,收益决定选择
最佳应对与占优策略
S是参与人甲的一个选择策略,T是参与人乙的一个选择策略。在收益矩阵中的某个单元格对应这策略组(S,T)
\(P_1(S,T)\)🚼🍼🅱️示参与人甲从这组决策获得的收益
\(P_2(S,T)\):表示参与人乙从这组决策获得的收益
最佳应对:针对参与人乙的策略T,若参与人甲采用策略S产生的收益大于等于自己的任何其他策略,则称参与人甲的策略S是参与人乙的策略的最佳应对
P1(S,T) ≥ P1(S’,T),其中\(S' \neq S\)
占优策略:对于另一参与人的每一策略都属于最佳应对
严格最佳应对:S会产生比任何策略应对T的其他策略都更高的收益,则称参与人甲的策略S是对于参与人乙的策略T的严格最佳应对。
严格占优策略:严格占优策略对于参与人乙的每一策略都是严格最佳应对
纳什均衡
假定参与人甲选择策略S,参与人乙选择策略T。若S是T的最佳应对,且T也是S的最佳应对,则称策略组(S,T)是一个纳什均衡。
在均衡状态,任何参与人都没有动机(理性的动机)去换另一种策略。
可以被看成是一种信念上的均衡,两者都不可能通过单方面改变策略而得到额外好处,尽管两人都改变可能会得到更好。
多重均衡
在一个博弈中存在多个均衡的情况。
如[猎鹿博弈](# 猎鹿博弈)
简单博弈的推理思路
如果两参与人都有严格占优策略,则可以预计他们均会采取严格占优策略
如果只有一个人参与严格占优策略,则这个参与人会采取严格占优策略,而另一方会采取此策略的最佳应对。
如果不存在严格占优策略,则应寻找纳什均衡
- 如果存在一个纳什均衡,则就对应合理结果
- 如果存在多个,就应该需要额外信息辅助决策
- 协调博弈,鹰鸽博弈等
零和博弈
两人扔硬币,若两人的面相同,则甲获得乙的硬币,反之相反
此时不存在纳什均衡
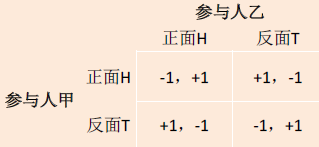
混合策略
引入随机性,考虑参与人将以一定的概率分布在不同策略间进行博弈,一种分布对应一个“混合策略”
对于双策略(H与T)博弈,混合策略则可简略表示为一个概率。纯策略就是概率为(0,1)的混合策略。
参与人1的策略是概率p,是指参与人以概率p执行H,以1-p执行T
参与人2的策略是概率q,是指参与人以概率q执行H,以1-q执行T
混合策略的收益
对于参与人1采用p概率执行H
若参与人2采用H,收益期望为
\(\overline{P_2} (p, H ) = p⋅ P2 (H, H )+ (1− p)⋅ P2 (T, H )\)
若参与人2采用T
\(\overline{P_2} (p, T ) = p⋅ P2 (H, T)+ (1− p)⋅ P2 (T, T)\)
混合策略的均衡
混合策略的纳什均衡:是一对混合策略,彼此都是对方的最佳应对
在混合策略中,有一个充要条件:双方都不存在纯策略的较优
即有
\(\overline{P_2}(p,H)=\overline{P_2}(p,T)\)
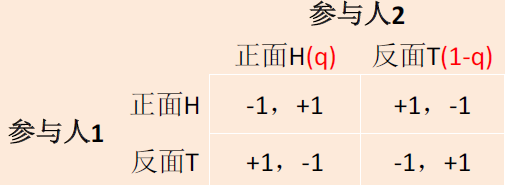
对于1,期望收益为\((-1)\times{q}+(1-q)=1-2q\)
对于2,期望收益为\(1\times(q)+(-1)(1-q)=2q-1\)
若不存在,则两者相等
对于混合策略均衡的求解,可见[持球抛球混合策略均衡](# 持球抛球混合策略均衡)
常见的博弈模型
囚徒困境
两个囚徒被怀疑是抢劫犯
如果两人坦白,则两人会因认罪每人关押4年
如果两人都不坦白,两人会以拒捕罪每人被判1年
如果两人一人坦白,一人不坦白,则坦白的人不被关押,不坦白的人会被关10年
(两人分开关押,没有交流)
| 抵赖 | 坦白 | |
|---|---|---|
| 抵赖 | 1,1 | 10,0 |
| 坦白 | 0,10 | 4,4 |
对于两个疑犯来说,严格占优策略都是坦白
说明了“有关个体私立前,建立合作是十分困难的”
兴奋剂博弈/军备竞赛
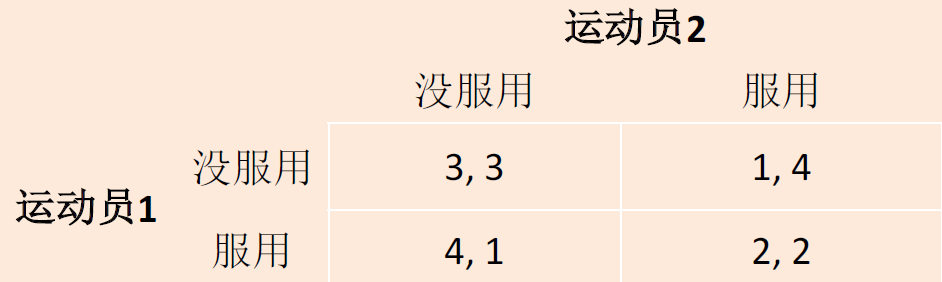
对于相同体能的运动员,若一方服用兴奋剂,则会在对决中取得较大优势
称为军备竞赛,竞争双方为保持彼此实力相当,都会选择生产更具威胁性的武器,尽管会对自身造成伤害。
营销战略博弈
三客户博弈是只有一方有严格占优策略的例子
某一种商品,分为廉价和高档次两种型号,所占市场比例为6:4
若两公司选择从一个型号上竞争,则瓜分一种型号所占的市场,否则瓜分两个市场,在同一市场竞争时,由于A公司信誉较好,可以比公司B占有更多的市场份额

此时对于公司1,廉价为严格占优策略,而对于公司二无严格占优策略,则需选择公司1廉价策略的最佳应对——高档次
三客户博弈
三客户博弈中,两者均无严格占优策略
两公司一、二,三客户,有目标客户A,B,C
如果两家公司找到一个客户,两者必须平分此次收益
公司一由于规模过小,只有和其他公司合作时才能完成客户要求
A客户只有在两公司合作下才能接下任务,此时总收益为8
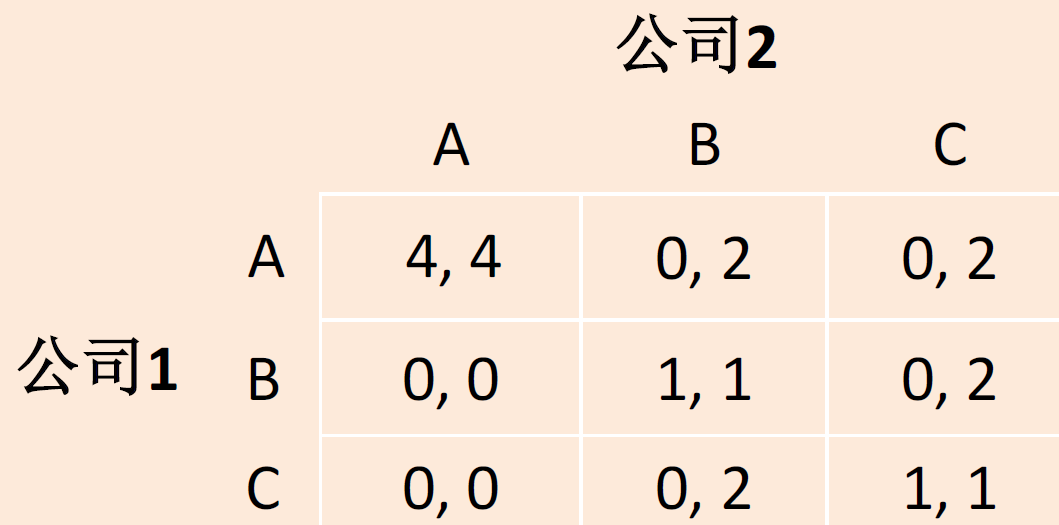
由上面的收益矩阵可知,两者均不存在最优策略
猎鹿博弈
两猎人外出猎物,若合作可以猎到鹿
每个人单飞可以猎到兔
如果一方想单独猎鹿,则收益是0.另一方依然能猎到兔
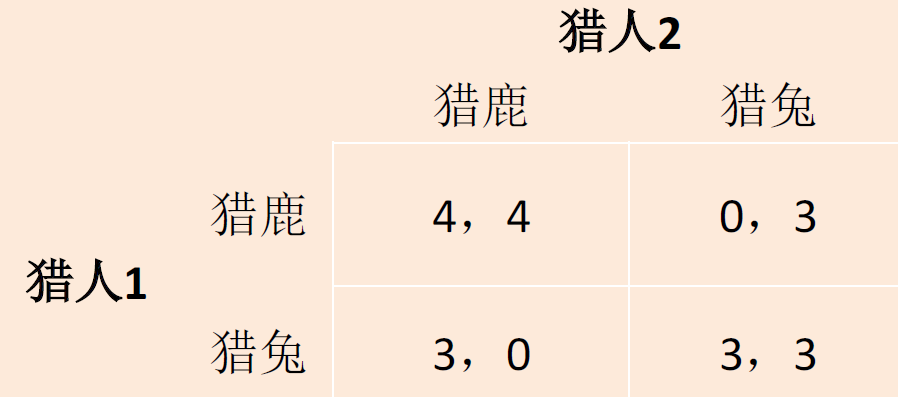
此时需要在高收益和由于另一方不合作造成损失之间进行权衡。
鹰鸽博弈
如果两者都不争夺,则平分食物
如果两者都争夺,食物会因打斗而浪费
如果一者争夺,会得到大部分食物
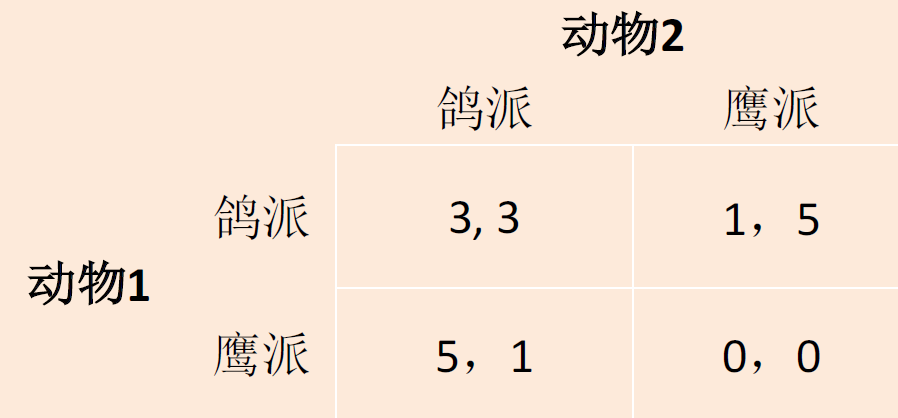
此时参与者的行为很难预测,由于(5,1)和(1,5)都是均衡
持球抛球混合策略均衡
帕累托最优
一个策略组被称为帕累托最优,若不存在其他策略组满足:所有参与者得到至少和目前一样高的回报,且至少有一个参与者得到严格较高的回报
存在3个帕累托最优,但都不是均衡
社会最优
一组策略选择是社会最优(或社会福利最大化),若它使参与者的回报之和(总收益)最大

(报告,报告)是社会最优
社会最优同时也是帕累托最优
用博弈论思想分析问题
重要的是理解不同博弈的类型,以及求解的基本方法。均衡是一个基本目标
对问题的要求进行准确地把握,并抽象成收益矩阵同时十分重要


 浙公网安备 33010602011771号
浙公网安备 33010602011771号