2 曲面表示法

曲面表示法

点采样形式/点云 Point Cloud

点云是空间（通常是三维空间）中一系列点的集合。点云数据通常可以由三维扫描仪得到，每个数据点的属性包括颜色和该处的法向量等。点云是一种原始数据，它只是一系列点的集合，并不显式地表示曲面。

体素 Voxels

体素是三维空间中的最小分割单位，通常利用二元值或是概率值来表示该位置的体素是否属于某个特定集合。我们可以用一个特定集合的体素来近似某物体的体积，从而表示物体的三维形状。

每个体素本身并不知道物体的整体形状是怎样的，物体的表面通过计算等值面通过的网格点来重建。

边界表示使用一组曲面来描述三维对象，这些曲面将物体分成内部和外部，从而精确描述物体型形状。本章涉及到的曲面表示法由多边形表示法、等等。

多边形网格形式 Polygonal Meshes

三维图像对象中运用边界表示最普遍的方式是使用一组包围对象内部的表面多边形。

任何多边形曲面都可以由一组多边形网格（polygon mesh）线性近似（piecewise linear approximation ）表示。每一个多边形网格都包含顶点、边界和曲面三种元素。

多边形网格可以用来近似任何拓扑结构(arbitrary topology)。

多边形近似的误差可表示为

\[O(h^{p+1}) \]

可以通过以下方式来提高多边形网格的近似质量：

• 增加p的数值： 使用高阶的多边形 (p method)
• 减小h的数值： 使用更小更多的分割 (h method)

所以在确定物体表面的拓扑结构之后要对多边形网格进行优化，尽可能在控制误差率的同时减少顶点的数目。为了更加细化表面结构，有时需要对多边形网格进行合适的细分（piecewise smooth subdivision surfaces）来获得平滑的表面。误差和多边形网格面的数目有关，面越多误差越小。(flexibility for adaptive refinement/piecewise smooth surfaces)

三角形网格

对于三角形网格来说，近似误差为

\[O(h^2) \]

h指最大边的长度。由于平方的存在，将边长减为原来的一半可以使得误差减为原来的1/4。每一次对三角形网格的细分都会将边长减半，面的数量会相应增加四倍，同时误差会减为原来的1/4。

Euler Formula states an interesting relation between the numbers of vertices V，edges E and faces/triangulation F in a closed and connected mesh

\[V - E + F= 2(1-g) \]

g is the genus of the surface. For typical mesh the genus is small compared to the number of elements, the right-hand side of Equation can be assumed to be almost zero. The mesh statistics:

\[F \approx 2V\\ E \approx 3E\\ \]

the average vertex valence is 6.

多边形网格易于渲染。

多边形网格的约束

多边形网格是满足某些约束的多边形的集合，并非任意多边形都可以加入多边形网格。

A triangle mesh is called manifold if:

• the intersection of two triangles is
  • empty
  • a common vertex
  • a common edge
• edge have
  • one adjacent - border edge
  • two adjacent triangle - inner adge
• for a vertex the adjacent triangles
  • build a single open fan - border vertex
  • build a single closed fan - inner vertex

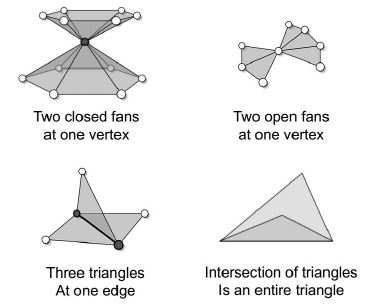
non - manifold meshes:

• two closed fans at one vertex
• two open fans at one vertex
• three triangles at one edge
• intersection of triangles is an entire triangle

多边形网格的拓扑和几何结构

Topology vs. Geometry

• Topologically equivalent but different geometry
• Geometrically equivalent but different topology

多边形网格的数据结构

算法中通常会用到的操作有：

• 访问个别的顶点、边和面。包括以特定顺序遍历某种元素
• 按一定方向遍历所有边
• 访问一条边的相关面
• 通过给定的边访问它的两个端点
• 给定一个顶点，访问所有邻域元素

一般多边形网格的数据结构都是基于边的，课程中主要用到了基于半边的数据结构和有向边数据结构。

Half-Edge Data Structure

For each half edge we store a reference to

• the vertex it points to
• the next half-edge of the face or boundary
• its inverse/opposite halfedge
• its adjacent face
• the previous half-edge in the face(optional)

在半边数据结构中，半边的方向是沿着每个面或者边界的逆时针方向。

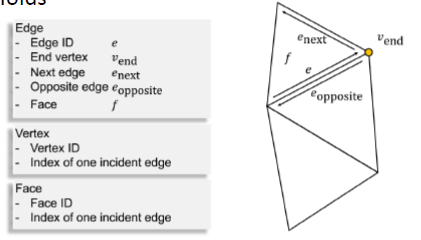
每个面存储一个半边的引用，每个顶点也存储一个半边的引用。而一个半边又可以让我们方便地遍历每个元素的所有周围元素。

directed Edge Data Structure

有向边数据结构是基于半边数据结构，专门为三角形网格设计的一种高效数据类型。

the directed edges data structure is a memory efficient variant of the half-edge data structure designed for triangle meshes. It has following restrictions:

• only triangle meshes can be represented
• There is no explicit representation of edges

The directed edges data structure is based on indices as reference to each element(vertex, face, half-edge).

如果某一个面的索引号为f，那么它三个半边的索引号分别为 3f+i, i=1,2,3

如果已知某半边的索引号为h，那么它相邻面的索引号为 h/3，它临边的索引号为 (h+1) mod 3

参数形式 Parametric Surface

所谓参数表示的曲线，即把空间中一点p的三个坐标都写成某个参数u的标量函数。而参数表示的曲线则是把曲面表示成双参数u和v的矢函数，即p=p(u,v)。因为可以实现任何形状的表面，所以此法多用于设计和建构过程。

曲面的参数表示：它用一个拥有两个参数的方程来表示一个欧几里得空间内的曲面。

(Parametric Surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters.)

\[f(u,v): R^2 \rightarrow R^3 \]

常见的有：贝塞尔曲线(Bezier-Spline)， B样条曲线(B-Spline)

贝塞尔曲线

假设给定n+1个控制点位置pk, k = 1,2,3...n，这些坐标点将混合产生下列位置向量p(u)，用来描述p0和pn间逼近多项式函数的路径：

\[P(u) = \sum_{k=0}^np_kBEZ_{k,n}(u) \\ u \in [0,1] \]

\[BEZ_{k,n}(u) = C_{n}^ku^k(1-u)^{n-k} \]

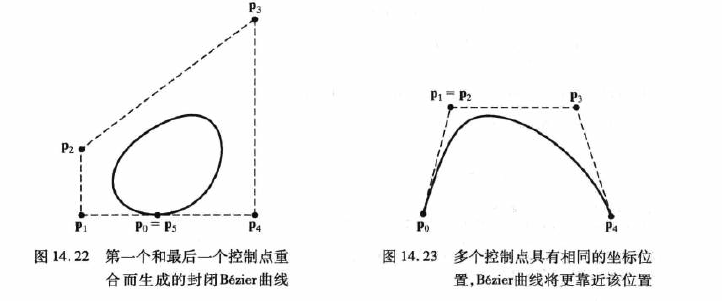
多数情况下，贝塞尔曲线是一个阶数比控制点少1的多项式：三点生成一个抛物线，四点生成一个三次曲线。贝塞尔曲线总是通过第一个和最后一个控制点，其一定会落在控制点的凸壳内。我们可以使用任何数目的控制点来拟合一条贝塞尔曲线。

贝塞尔曲面

可以使用两组正交的贝塞尔曲线来设计一个对象曲面。贝塞尔曲面的参数向量函数可以按照贝塞尔混合函数的张量积形式来描述：

\[P(u,v) = \sum_{j=0}^m\sum_{k=0}^np_{j,k}BEZ_{j,m}(v)BEZ_{k,n}(u) \]

p_jk指定了(m+1)*(n+1)个控制点的位置。常数u的曲线时通过u取单位内一定值并将v从0变到1绘制出的。常数v的曲线绘制也类似。

非参数表示分为隐式形式和显式形式。

隐式形式 Implicit Surface

存在一个方程f，使得空间中的每个点对应于一个标量值。曲面则由方程f的水平集定义。例如，给定曲面上一点p及其法向量n，曲面上的点应满足：

\[f(x,y,z) = ((x,y,z) - \vec p )*\vec n = 0 \]

f 又叫符号距离函数(signed distance function)

符号距离函数

符号距离函数的构造方法

• 给定一组采样点
• 寻找一个方程f，使得方程f满足以下条件
  • 在采样点处 f=0
  • 在物体内部 f<0
  • 在物体外部 f>0

Hoppe's 92

\[f(x) = (\vec x - \vec p)*\vec n_p \]

• 分段线性近似(piecewise linear surface approximation)

• 在多边形边界处存在不连续性

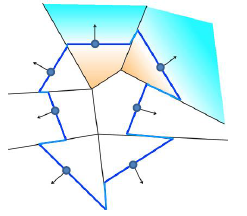
• 其效果受采样点密度影响(depend on input density)

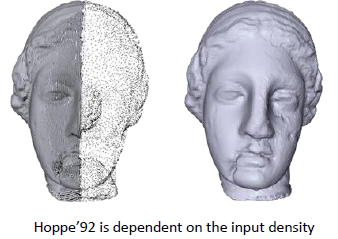
我们给符号构造函数增加一个新约束以获得较好的表面效果

符号距离函数的构造方法

• 给定一组采样点
• 寻找一个方程f，使得方程f满足以下条件
  • 在采样点处 f=0
  • 在物体内部 f<0
  • 在物体外部 f>0
  • 方程f应当平滑

径向基函数(Radial Basis Function)

复杂函数可以用不同尺度、不同位置的核函数的和来近似

\[g(x) = f(x) = \sum_i a_i\phi_i(x) = \sum_ia_i\phi(\lVert x - c_i\rVert) \]

径向基函数可以实现任意复杂度的方程。如果我们所用的核函数是平滑的，那么最终复现的方程也是平滑的。为了实现对线性方程的模拟，我们在函数最后加上一个线性项

\[f(\vec x) = \sum_i a_i\phi_i(\vec x) + \vec b*\vec x + d\\ \phi_i(\vec x ) = \lVert \vec p_i - \vec x\rVert \]

在上式中，a_i,b,d是未知量。在三维空间中，如果有n个采样点，我们将有n+4个未知数。

根据符号距离函数的约束可知，在采样点附近f(x)的值应当等于零。由此可以的到n个等式，但由此构造的方程组是一个欠定方程组(underdetermined system)，由此我们需要增加新的约束：对于每一个采样点，我们随机获取一个新点，使这些新点在表面法向量的方向上正向或反向移动距离epsilon，由此得到另外n个等式，此时我们构造的方程组是一个超定方程组，通过求最小二乘解可以得到未知数的值。

Hoppe和RBF方法对比：

• Hoppe：局部算法，计算速度快，不能处理噪声、外点影响
• RBF：全局算法，计算速度慢，可以应对噪声、外点影响

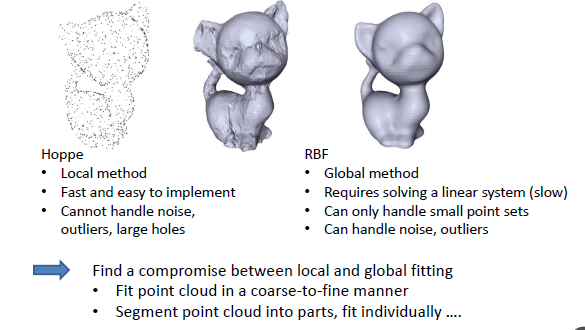
RBF with floating centers

Poisson Reconstruction

符号距离函数的渲染

获取等高面的方法

• Ray Marching

  固定步长，线性插值得到零点。

• Sphere Tracing

  动态步长，如果距离曲面的距离小于某个阈值则停止。

将等高面转换为多边形网格 - Marching Cubes

Marching Cubes is a popular algorithm for iso-surface extraction(creating a polygonal mesh from a voxel model)

The input of the MC algorithm is a voxelization representing a scalar field v = f(x,y,z). The input scalar field might be binary(or not). If the input data is not binary ,MC requires an additional parameter to classify samples as inside/outside the surface.

Traverse all cubes formed by 2x2x2 neighboring samples.For each cube, MC generates a set of triangles corresponding to the output iso-surface inside the cube.

每个立方体有8个顶点，每个顶点的取值有两种可能，八个顶点组成的编码共有 2^8=256种可能。但其中有很多种组合是对称的，我们可以将对称的情况归为一类，最终简化成14种类型，见下图：

对于每一个立方体，我们都要生成等高面的顶点和对应组成的三角形。

生成顶点：线性插值法

假设标量场是连续的，那么等高面所过的顶点可以用线性插值的方式来求。定点可以位于立方体12条边中的任意一条。

\[P = P_1\frac{v-v2}{v2-v1} + P_2\frac{v-v1}{v2-v1} \]

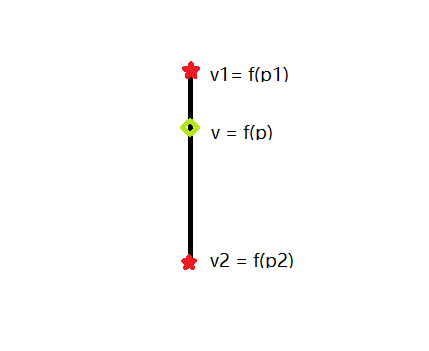
某些情境下可能不能唯一确定面的构成（有歧义存在）

生成三角形： 查表法（LOOK-UP-TABLE）

MC的表格中包含了256种情况，对应之前所提到的8个顶点取值的所有可能。对于每一种情况，表格中都保存着相应的三角形构造方法。例如：

左下图的顶点代码应为 0011 0011，转十进制换算后得到是config51

查表，得到config51中的三角形构造为{{8,9,10},{9,11,10}}

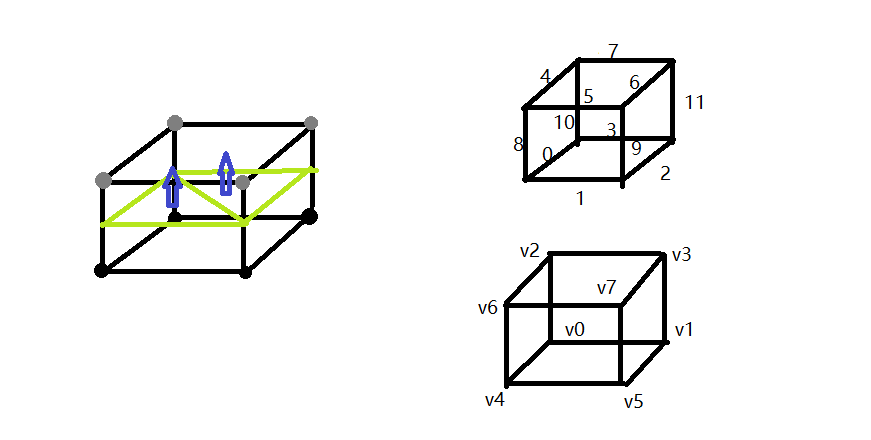
在有歧义的情况下，选择最简单的构造方法。

显式形式 Explicit Surface

直接用方程描述曲线/曲面的形状

例如，对于直线来说：

\[f(x) = y=mx+c \]

对于曲面来说，定义 z=f(x,y)， 那么曲面可以表示为

\[S(x,y) = (x,y,f(x,y)) \]

直接法对可以表示的曲面有一定限制，比如每一个(x,y)点对只能有一个高度值，不能表示多值曲面。

应用场景主要有：

• 高度场(height field)

构造实体几何 Constructive Solid Geometry

构造实体几何是实体造型中应用的一项技术。在构造实体几何中，建模人员可以使用逻辑运算符(Boolean operators)并、交或差操作将不同物体组合成复杂的曲面或球体。物体表面可由计算实体边界得到。