13年12月CCF_CSP
CSP冲冲冲
acwing 3192
- 出现次数最多的数
给定 nn 个正整数,找出它们中出现次数最多的数。
如果这样的数有多个,请输出其中最小的一个。
输入格式
输入的第一行只有一个正整数 nn,表示数字的个数。
输入的第二行有 nn 个整数 s1,s2,…,sns1,s2,…,sn。
相邻的数用空格分隔。
输出格式
输出这 nn 个次数中出现次数最多的数。
如果这样的数有多个,输出其中最小的一个。
数据范围
1≤n≤10001≤n≤1000,
1≤si≤100001≤si≤10000
输入样例:
6
10 1 10 20 30 20
输出样例:
10
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1e4+10;
int a[maxn];
int main()
{
int n,t;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>t;
a[t]++;
}
int maxx=0,p=0;
for(int i=1;i<=10000;i++)
{
if(a[i]>maxx)
{
maxx=a[i];
p=i;
}
}
printf("%d\n",p);
return 0;
}
acwing 3193
\3193. ISBN号码
每一本正式出版的图书都有一个 ISBN 号码与之对应。
ISBN 码包括 99 位数字、11 位识别码和 33 位分隔符,其规定格式如 x-xxx-xxxxx-x,其中符号 - 是分隔符(键盘上的减号),最后一位是识别码,例如 0-670-82162-4 就是一个标准的ISBN码。
ISBN 码的首位数字表示书籍的出版语言,例如 00 代表英语;第一个分隔符 - 之后的三位数字代表出版社,例如 670670 代表维京出版社;第二个分隔之后的五位数字代表该书在出版社的编号;最后一位为识别码。
识别码的计算方法如下:
首位数字乘以 11 加上次位数字乘以 22……以此类推,用所得的结果 mod11mod11,所得的余数即为识别码,如果余数为 1010,则识别码为大写字母 XX。
例如 ISBN 号码 0-670-82162-4 中的识别码 44 是这样得到的:对 067082162067082162 这 99 个数字,从左至右,分别乘以 1,2,…,91,2,…,9,再求和,即 0×1+6×2+……+2×9=1580×1+6×2+……+2×9=158,然后取 158mod11158mod11 的结果 44 作为识别码。
编写程序判断输入的 ISBN 号码中识别码是否正确,如果正确,则仅输出 Right;如果错误,则输出是正确的 ISBN 号码。
输入格式
输入只有一行,是一个字符序列,表示一本书的 ISBN 号码(保证输入符合 ISBN 号码的格式要求)。
输出格式
输出一行,假如输入的 ISBN 号码的识别码正确,那么输出 Right,否则,按照规定的格式,输出正确的 ISBN 号码(包括分隔符 -)。
输入样例1:
0-670-82162-4
输出样例1:
Right
输入样例2:
0-670-82162-0
输出样例2:
0-670-82162-4
#include <iostream>
using namespace std;
int main()
{
string s;
cin>>s;
int k=1,ans=0;
for(int i=0;i<11;i++)
{
if(i==1 || i==5) continue;
ans=ans+(s[i]-'0')*k;
k++;
}
ans=ans%11;
if(ans==s[12]-'0' || (ans==10 && s[12]=='X'))
printf("Right");
else
{
if(ans==10) s[12]='X';
else s[12]='0'+ans;
cout<<s;
}
return 0;
}
acwing 3194
\3194. 最大的矩形
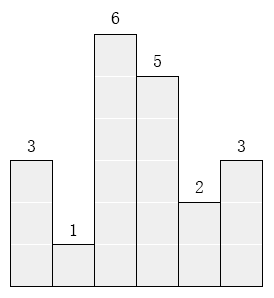
在横轴上放了 nn 个相邻的矩形,每个矩形的宽度是 11,而第 ii(1≤i≤n1≤i≤n)个矩形的高度是 hihi。
这 nn 个矩形构成了一个直方图。
例如,下图中六个矩形的高度就分别是 3,1,6,5,2,33,1,6,5,2,3。
请找出能放在给定直方图里面积最大的矩形,它的边要与坐标轴平行。
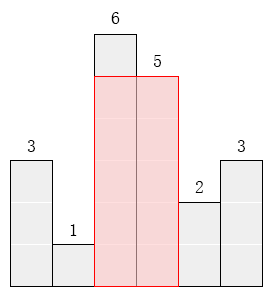
对于上面给出的例子,最大矩形如下图所示的阴影部分,面积是 1010。
输入格式
第一行包含一个整数 nn,即矩形的数量。
第二行包含 nn 个整数 h1,h2,…,hnh1,h2,…,hn,相邻的数之间由空格分隔。hihi 是第 ii 个矩形的高度。
输出格式
输出一行,包含一个整数,即给定直方图内的最大矩形的面积。
数据范围
1≤n≤10001≤n≤1000,
1≤hi≤100001≤hi≤10000
输入样例:
6
3 1 6 5 2 3
输出样例:
10
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1010;
int a[maxn];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
int maxx=n,cnt=0;
for(int i=2;i<=10000;i++)
{
cnt=0;
for(int j=1;j<=n+1;j++)
{
if(a[j]>=i)
{
cnt++;
}
else
{
maxx=max(maxx,i*cnt);
cnt=0;
}
}
}
cout<<maxx;
return 0;
}
acwing 3195
\3195. 有趣的数
我们把一个数称为有趣的,当且仅当:
- 它的数字只包含 0,1,2,30,1,2,3,且这四个数字都出现过至少一次。
- 所有的 00 都出现在所有的 11 之前,而所有的 22 都出现在所有的 33 之前。
- 最高位数字不为 00。
因此,符合我们定义的最小的有趣的数是 20132013。
除此以外,44 位的有趣的数还有两个:20312031 和 23012301。
请计算恰好有 nn 位的有趣的数的个数。
由于答案可能非常大,只需要输出答案除以 109+7109+7 的余数。
输入格式
输入只有一行,包括恰好一个正整数 nn。
输出格式
输出只有一行,包括恰好 nn 位的整数中有趣的数的个数除以 109+7109+7 的余数。
数据范围
4≤n≤10004≤n≤1000
输入样例:
4
输出样例:
3
思路:递推
需要满足以下的条件
0在1之前
2在3之前
则有以下6种状态
0-- 0 1 (2) 3 出现2
1-- (0) 1 (2) 3 出现0和2
2-- 0 1 (2) (3) 出现2和3
3-- (0) (1) (2) 3 出现0,1,2
4-- (0) 1 (2) (3) 出现0,2,3
5-- (0) (1) (2) (3) 出现0,1,2,3
f[i][0]表示0状态的次数,只有一个数的时候次数为1
f[i][1]表示1状态的次数,填充第i位使得状态为1状态。
有两种情况如果是0状态则只能填充(0),如果是1状态本身,则可以填充(0)或者(2)所以
f[i][1]=(f[i-1][1]*2+f[i-1][0])%mod;
#include <iostream>
using namespace std;
typedef long long ll;
const int maxn = 1010;
const int mod = 1e9+7;
ll f[maxn][6];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
f[i][0]=1;
f[i][1]=(f[i-1][1]*2+f[i-1][0])%mod;
f[i][2]=(f[i-1][2]+f[i-1][0])%mod;
f[i][3]=(f[i-1][3]*2+f[i-1][1])%mod;
f[i][4]=(f[i-1][4]*2+f[i-1][2]+f[i-1][1])%mod;
f[i][5]=(f[i-1][5]*2+f[i-1][4]+f[i-1][3])%mod;
}
cout<<f[n][5];
return 0;
}
acwing 3196dfs

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 55;
int n,m;
char g[N][N];
bool st1[N][N],st2[N][N];
int dx[] = {-1,0,1,0},dy[]={0,1,0,-1};
bool check(int x,int y,int k)
{
char c=g[x][y];
if(c=='+' || c=='S' || c=='T') return true;
if(c=='-' && k%2==1) return true;
if(c=='|' && k%2==0) return true;
if(c=='.' && k==2) return true;
return false;
}
void dfs1(int x,int y)
{
st1[x][y]=true;
for(int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a<0 || a>=n || b<0 || b>=m || g[a][b]=='#') continue;
if(st1[a][b]) continue;
if(check(x,y,i)) dfs1(a,b);
}
}
void dfs2(int x,int y)
{
st2[x][y]=true;
for(int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a<0 || a>=n || b<0 || b>=m || g[a][b]=='#') continue;
if(st2[a][b]) continue;
if(check(a,b,i^2)) dfs2(a,b);
}
}
int main()
{
cin>>n>>m;
int tx,ty;
for(int i=0;i<n;i++) cin>>g[i];
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
if(g[i][j]=='S') dfs1(i,j);
else if(g[i][j]=='T')
{
tx=i,ty=j;
dfs2(i,j);
}
}
if(!st1[tx][ty]) puts("I'm stuck!");
else
{
int res=0;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
if(st1[i][j] && !st2[i][j])
res++;
cout<<res<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号