求正数数组的最小不可组成和（Java实现，01背包衍生问题）

目录

• • 题目
  • 思路与代码展示
  • • 与01背包的思路转换
    • 二维数组代码展示
    • • 二维数组示意图
    • 优化代码

题目

• 链接

牛客：求正数数组的最小不可组成和

• 题目

给定一个全是正数的数组arr，定义一下arr的最小不可组成和的概念： 1，arr的所有非空子集中，把每个子集内的所有元素加起来会出现很多的值，其中最小的记为min，最大的记为max； 2，在区间[min,max]上，如果有一些正数不可以被arr某一个子集相加得到，那么这些正数中最小的那个，就是arr的最小不可组成和； 3，在区间[min,max]上，如果所有的数都可以被arr的某一个子集相加得到，那么max+1是arr的最小不可组成和；
举例： arr = {3,2,5} arr的min为2，max为10，在区间[2,10]上，4是不能被任何一个子集相加得到的值中最小的，所以4是arr的最小不可组成和； arr = {3,2,4} arr的min为2，max为9，在区间[2,9]上，8是不能被任何一个子集相加得到的值中最小的，所以8是arr的最小不可组成和； arr = {3,1,2} arr的min为1，max为6，在区间[2,6]上，任何数都可以被某一个子集相加得到，所以7是arr的最小不可组成和； 请写函数返回arr的最小不可组成和。

题目很啰嗦，但是想表达的意思很简单：

• 给定一个数组 arr；
• 得到这个数组 子集 的最大值和最小值；
• 在这个最大值和最小值区间内，找出数组任意几个数的和不能出现在这个区间的最小值，如果没有输出最大值加1；

• 输入

int[] arr = {3,2,4};

• 输出

8

• 解释

最大值为 9 ，最小值为 2；
3；
3 + 2 = 5；
3 + 4 = 7；
2； 2+ 4 = 6；
4，
能够组成的值有 2，3，4， 5， 6 ，7 ，9 在 [2，9] 这个区间内，8 是不可能组成的最小和。

思路与代码展示

这道题刚开始没看出来是01背包问题，我们需要做的是 枚举 出数组中所有数字能够组成的 和，然后找到 最小的不可能组成的和。该怎么枚举呢？我尝试过使用 dfs ，然后 回溯，但是没做出来。后来看了一下解析，想到了使用 动态规划 ，也就是 01背包 模型来完成。

与01背包的思路转换

arr[i] ==> 物品；
在最大值和最小值区间内 ==> 背包容量；
找到数组中最小不可能组成和 ==> 找到最小不可能装满的背包。

1. 查找得到最大值最小值；
2. 定义二维数组 int[][] dp = new int[arr.length+1][max+1]，初始化 dp[1][1] = 1；
3. 进行递推
4. 查询结果

二维数组代码展示

    public static int getFirstUnFormedNum(int[] arr) {
        // 1. 找到最大值和最小值
        int max = 0;
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < arr.length; i++) {
            max += arr[i];
            if (min > arr[i]) {
                min = arr[i];
            }
        }

        // 2. 定义 dp 数组
        int[][] dp = new int[arr.length+1][max+1];
        // 初始化
        dp[1][1] = 1;

        // 3. 递推
        for (int i = 1; i <= arr.length; i++) {
            for (int j = 1; j <= max; j++) {
            	// 小于情况下
                if (j < arr[i-1]) {
                    dp[i][j] = dp[i-1][j];
                }
                // 等于情况下
                else if (j == arr[i-1]) {
                    dp[i][j] = 1;
                }
                // 大于情况下
                else {
                    if (dp[i-1][j-arr[i-1]] == 1) {
                        dp[i][j] = 1;
                    }else if (dp[i-1][j] == 1) {
                        dp[i][j] = 1;
                    }
                    else {
                        dp[i][j] = 0;
                    }
                }
            }
        }

        // 查看二维数组
        for (int i = 0; i <= arr.length; i++) {
            for (int j = 0; j <= max; j++) {
                System.out.print(dp[i][j] + " ");
            }
            System.out.println();
        }

        // 4. 查询结果 结果在最后一行
        int index = arr.length;
        for (int i = min; i <= max; i++) {
            if (dp[index][i] != 1) {
                return i;
            }
        }
        return max+1;
    }

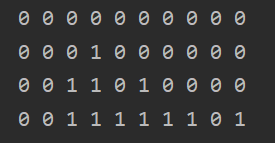
二维数组示意图

优化代码

    public static int getFirstUnFormedNum2(int[] arr) {
        // 全是正数的 arr
        // i 代表物品
        // j 代表背包容量
        // 目地: 找出数组中最小不可能组成和
        //       ==> 找出最小不能被填满的背包

        // 1. 得到最大最小值
        int max = 0;
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < arr.length; i++) {
            max += arr[i];
            if (min > arr[i]) {
                min = arr[i];
            }
        }

        // 2. 定义 dp 数组
        boolean[] dp = new boolean[max+1];
        // 初始化
        dp[0] = true;

        // 3. 递推过程
        for (int i = 0; i < arr.length; i++) {
            for (int j = max; j >= arr[i]; j--) {
                // 当 j == arr[i] 的时候, j - arr[i] 代表自己能够到达的下标 2-2 = 0
                // 第一个为 T 的是 3, 当 j == 3 的时候, j - arr[i] = 0;
                // 第二个位 T 的是 5, 当 j == 5 的时候, j - arr[i] = 3;
                // 第三个为 T 的是 2, 当 j == 2 的时候, j - arr[i] = 0;
                // 第四个为 T 的是 9, 当 j == 9 的时候, j - arr[i] = 5;
                // 第五个为 T 的是 7, 但 j == 7 的时候, j - arr[i] = 3;
                // 第六个为 T 的是 6, 当 j == 6 的时候, j - arr[i] = 2;
                // 第七个为 T 的是 4, 当 j == 4 的时候, j - arr[i] = 0;
                dp[j] = dp[j-arr[i]] || dp[j];
                // dp[j-arr[i]] 代表 "拿" 当前数字
                // dp[j] 代表不拿当前数字 比如 5 的时候, dp[5] || dp[5-1] 原来 dp[5] 是 T dp[1] 是 F, 所以这个时候 "不拿"
            }
        }

        // 打印数组
        System.out.println(Arrays.toString(dp));

        // 4. 查询结果
        for (int i = min; i < dp.length; i++) {
            if (!dp[i]) {
                return i;
            }
        }
        return max + 1;
    }