RNN学习笔记

Introduction of Recurrent Neural Network

Basic concept

论语中有 “学而不思则罔，思而不学则殆”。其中 “学而不思则罔” 这句话指的是如果我们在读书的过程中，对书本的内容不加以思考和理解，我们就无法有效地利用书本的知识。人类本身就是善于应用自己所学知识来解决问题的动物。当我们读某本书某篇论文，我们会根据已经阅读过的内容来对后面的内容进行理解，而不会把已经理解的内容丢掉从头思考，毕竟我们对内容的理解是贯穿的。

但是，传统的Neural Network (NN)还无法做到这一点。（i.e., 无法通过上下文来预测某个将要出现的单词）因为传统的NN没用保存信息的作用。幸运的是，我们可以通过构建一种循环的结构来允许信息保存一段时间。

那就是Recurrent Neural Network (RNN) 。字面意思可以翻译为循环神经网络。为什么称为循环神经网络？如图下所示：

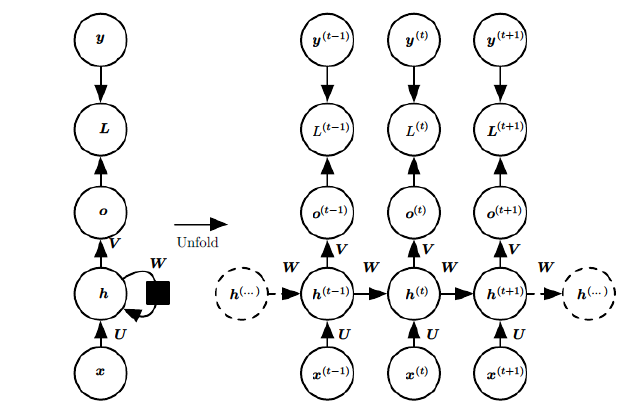
上图的左边是未展开的RNN,右图为展开式的RNN.其中\(X_t\) 是 \(t\) 时刻训练样本的输入， \(h_t\) 是隐藏层， \(o_t\) 是隐藏层的加权输入， \(L_t\) 为损失函数，\(y_t\) 为真实值。 可以看到，隐藏层的输出一部分用作输出（作为下一层网络的输入）， 一部分以下一刻输入的形式重新回到隐藏层当中。

如果把上图用公式表示的话：

首先对单个时刻的网络进行公式化（前向传播）：

\( h_t = tanh( Ux_t + Wh_{t-1} + b) （1） \)
\( o_t = Vh_t + c （2） \)
\( y~t = softmax( o_t ) (预测输出） （3） \)

如果将式（1）反复代入（2）中：

\( o_t = Vh_t + c \)
\( = V（tanh( Ux_t + Wh_t-1 + b) ）+ c \)
\( = V（tanh( Ux_t + W（tanh( Ux_t-1 + Wh_t-2 + b) ） + b) ）+ c \)
\( = V（tanh( Ux_t + W（tanh( Ux_t-1 + W（tanh( Ux_t-2 + Wh_t-3 + b) ） + b) ） + b) ）+ c \)
这就是为什么称为循环神经网络。

Update procedure/method of RNN

如果要让我们的网络学习通过上下文来预测一个词语或单词，我们需要对网络进行训练。这里的训练指的是对网络中的参数（i.e., \(W, V, U, c, b\)）进行不断地更新（学习过程），使网络的输出值更加接近真实值。上面我们已经有了前向传播公式的基础，接下来可以通过back propagation (BP, 反向传播) 来对网络进行训练。实际上对于RNN来说，反向传播并严谨，毕竟RNN是时间序列的模型，所以应该是 BPTT (back propagation through time)。

首先定义我们的损失函数为 Cross entropy Error Function (交叉熵损失函数), 输出层的激活函数很自然就是 softmax 函数（毕竟是预测，那就是求每个可能出现的单词的概率），隐藏层为 tanh 函数。

在RNN当中，每个时刻都有一个对应的损失， 所以总的损失是：

\(L = \sum_{t = 1}^{\tau }L^t\)

我们可以先对 \(V\) 和 \(c\) 进行梯度计算。因为它们仅与当前时刻的输出有关。

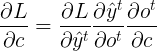
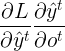部分为 Cross entropy 求偏导， 这里直接给出结果 ,对c求偏导为1，所以最后结果为:

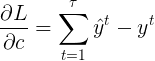
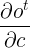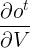同样的，对V的梯度只是换成，所以
.

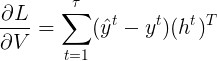因为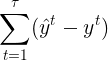是列向量，所以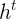转置为行向量。

接下来对\(W，U，b\)进行梯度计算。相对于\(V\)和\(b\)来说，\(W, U, b\)的梯度相对复杂。
首先我们来考虑\(W\)的梯度，因为上面已经定义了总的损失，所以对\(W\)的总损失可以表示为：

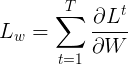
现在试着展开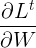。根据链式法则：

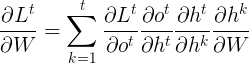
为什么时求和？
因为对于时刻\(t\)的梯度损失是所有经过的时刻的损失的总和。也可以理解为，当前时刻的梯度变化是由所有经过的时刻的梯度来决定的，每一时刻所产生的变化都对现在当前时刻的梯度有所影响（这也是为什么要求偏导数，因为我们需要知道每一部分的变化对总体的影响）。
上述式子中：

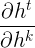
是当前时刻对\(k\)时刻的偏导，这里可以继续展开为：

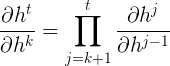
例如当前时刻\(t=3\)，当\(k=1\)时:

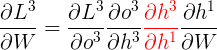
其中
\(h^1\)的函数是\(h^2\), \(h^2\)的函数又是\(h^3\)，所以这里又可以根据链式法则写成：

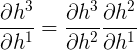
所以某时刻对\(W\)的梯度损失可以表达为：

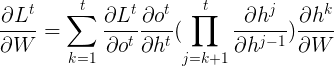
其中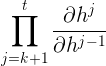是函数向量对向量求偏导，因为：

\( h_t = tanh( Ux_t + Wh_{t-1} + b) \)

可以表示为：

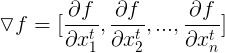
这里函数也是用向量中的每个元素求和组成的，所以可以进一步写成Jacobian矩阵：

除对角线外，其余偏导数为0，所以:

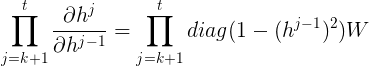
激活函数tanh和它的导数图像如下：

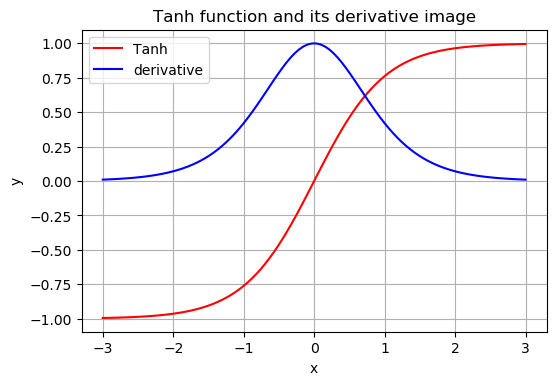
当时间序列\(t\)越大的情况, 如果tanh的偏导数小于1，矩阵\(W\)也小于1的话，距离当前时刻很远的参数的梯度将无限趋于0，这时神经网络的梯度损失由最近距离的梯度所主导，导致网络无法学到（更新）远距离的参数，即模型无法学到一开始的知识。这就是所谓的“梯度消失”。
相反，如果矩阵\(W\)中的元素不是小于1，即便tanh的偏导数是很小，累乘项也难以保证tanh'与矩阵的乘积在1附近，因为矩阵\(W\)与tanh'的乘积偶尔出现一两项大于1都会导致数值脱离0~1的范围，随着\(t\)的增大, 梯度大于1，即“梯度爆炸”。