线性代数-矩阵乘积

一、点积

概念：相同位置的按元素乘积的和，可以通过dot()函数调用

y = torch.ones(4, dtype=torch.float32)
print(y)
print(x)

# 点积：相同位置的按元素乘积的和
print(torch.dot(x, y))

# 可以通过执行元素乘法，然后进行求和来表示两个向量的点积
print(x*y)
print((x*y).sum())

#输出结果

tensor([1., 1., 1., 1.])
tensor([0., 1., 2., 3.])
tensor(6.)
tensor([0., 1., 2., 3.])
tensor(6.)

　　

二、矩阵-向量积

1、调用mv函数求矩阵向量积

2、矩阵向量积 𝐀𝐱 是一个长度为 𝑚 的列向量，其第 𝑖 个元素是点积（都是1行n列，可以做点积，最后得到一个标量）

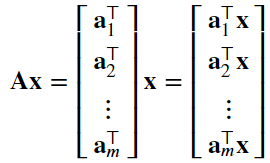
# torch.mv是矩阵与向量积

print(A)
print(x)
print(torch.mv(A,x))
A.shape, x.shape, torch.mv(A, x)
# A是5行4列的元素，x是一个有四个元素的向量

#输出结果

tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [12., 13., 14., 15.],
        [16., 17., 18., 19.]])
tensor([0., 1., 2., 3.])
tensor([ 14.,  38.,  62.,  86., 110.])
(torch.Size([5, 4]), torch.Size([4]), tensor([ 14.,  38.,  62.,  86., 110.]))

　　

三、矩阵-矩阵乘法

1、调用mm函数求矩阵的乘法

2、注意矩阵乘法与哈达玛积的区别

3、哈达玛积：将两个矩阵按元素乘积

# torch.mm：矩阵的乘法，行与列相乘

B = torch.ones(4, 3)
print('我是B矩阵\n',B)
print('我是A矩阵\n',A)

torch.mm(A, B)

#输出结果

我是B矩阵
 tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])
我是A矩阵
 tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [12., 13., 14., 15.],
        [16., 17., 18., 19.]])
tensor([[ 6.,  6.,  6.],
        [22., 22., 22.],
        [38., 38., 38.],
        [54., 54., 54.],
        [70., 70., 70.]])

　　

四、范数

1、一个向量的范数告诉我们一个向量的大小。这里考虑的大小（size）概念不涉及维度，而是分量的大小

2、L2范数：向量元素平方和的平方根

3、范数只能计算浮点数类型

# ‖𝐱‖就是x向量元素平方和的平方根
# 在深度学习中，我们更经常地使用  𝐿2  范数的平方。

u = torch.tensor([3.0, -4.0])
v = torch.tensor([[4,3],[6,8]])
print(u)
print(v)


# 使用 norm 来求L2范数
torch.norm(u)

#torch.norm(v):如果对其求范数会报错

#输出结果
tensor([ 3., -4.])
tensor([[4, 3],
        [6, 8]])
tensor(5.)

4、L1范数：表示为向量元素的绝对值之和

# L1范数是向量各元素的绝对值之和
print(u)
print(u.abs())
print(abs(u))

torch.abs(u).sum()

#输出结果

tensor([ 3., -4.])
tensor([3., 4.])
tensor([3., 4.])
tensor(7.)

5、弗罗贝尼乌斯范数：计算矩阵元素平方和的平方根

# 弗罗贝尼乌斯范数：可以用来计算矩阵元素平方和的平方根
# 使用norm（）函数来调用

torch.norm(torch.ones((2, 2)))

#输出函数

tensor(2.)