算法day38-动态规划（11）

目录

1. 最长公共子序列
2. 不相交的线
3. 最大子序和
4. 判断子序列

一、最长公共子序列（不要求元素之间连续）

 https://leetcode.cn/problems/longest-common-subsequence/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp = new int[text1.length()+1][text2.length()+1];
        for(int i=1; i<text1.length()+1; i++){
            for(int j=1; j<text2.length()+1; j++){
                if(text1.charAt(i-1) == text2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1]+1;                    
                }else{
                    dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j]);
                }
            }
        }
        return dp[text1.length()][text2.length()];
    }
}

 

二、不相交的线

 https://leetcode.cn/problems/uncrossed-lines/?envType=problem-list-v2&envId=8At1GmaZ

 

 

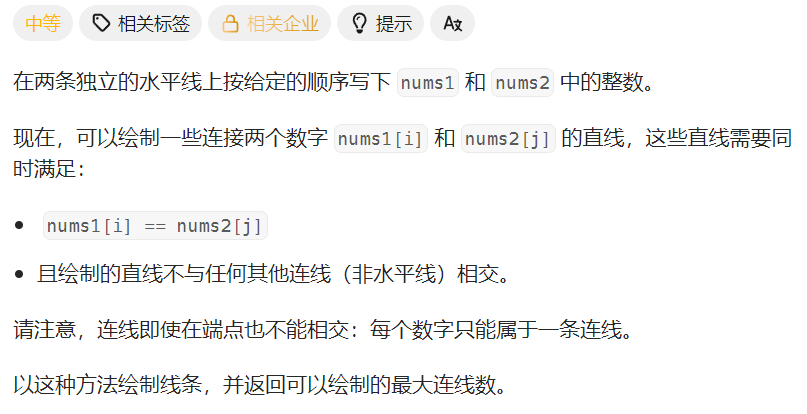
class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length+1][nums2.length+1];
        for(int i=1; i<nums1.length+1; i++){
            for(int j=1; j<nums2.length+1; j++){
                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1]+1;
                }else{
                    dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j]);
                }
            }
        }
        return dp[nums1.length][nums2.length];
    }
}

 

三、最大子序和

 https://leetcode.cn/problems/maximum-subarray/?envType=problem-list-v2&envId=8At1GmaZ

 　　这道题用贪心的做法也可以做，代码如下：

class Solution {
    public int maxSubArray(int[] nums) {
        int minPrefix = 0; 
        int maxSubSum = Integer.MIN_VALUE;
        int prefix = 0;
        for (int num : nums) {
            prefix += num;      //求当前的前缀和
            // 用当前最大的前缀和 - 前面最小的前缀和
            maxSubSum = Math.max(maxSubSum, prefix - minPrefix);
            minPrefix = Math.min(minPrefix, prefix);
        }
        return maxSubSum;
    }
}

　　用动态规划的做法：

class Solution {
    public int maxSubArray(int[] nums) {
        //dp[i]：以nums[i]结尾的最大连续子数组的和
        //两种情况：延续前面的；不延续前面的
        int[] dp = new int[nums.length+1];
        int res = nums[0];
        dp[0] = nums[0];
        for(int i=1; i<nums.length; i++){
            dp[i] = Math.max(dp[i-1]+nums[i], nums[i]);
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

 

四、判断子序列

 https://leetcode.cn/problems/is-subsequence/?envType=problem-list-v2&envId=8At1GmaZ

 

1. 定义状态：

• dp[i][j] 表示 s 的前 i 个字符是否能在 t 的前 j 个字符中找到，且保持顺序一致。

2. 状态转移：

• 初始化 dp[0][j] = 0，即当 s 是空字符串时，t 的任何前缀都能包含空字符串。

• 初始化 dp[i][0] = 0，即当 t 是空字符串时，只有当 s 也是空字符串时才能为子序列。

• 对于每一对字符 (i, j)：

  • 如果 s[i-1] == t[j-1]，说明这两个字符相等，我们可以将 dp[i-1][j-1] 的值加 1，表示 s 的前 i 个字符中，t 的前 j 个字符中可以找到 s[i-1]。

  • 否则，dp[i][j] 等于 dp[i][j-1]，表示我们可以通过删除 t[j-1] 来保持 s 的顺序。

3. 最终结果：

• 当遍历完所有字符后，dp[s.length()][t.length()] 记录了 s 是否能在 t 中作为子序列出现。如果它等于 s.length()，则说明 s 是 t 的子序列。

4. 时间复杂度：

• 时间复杂度是 O(m * n)，其中 m 和 n 分别是字符串 s 和 t 的长度。由于我们需要遍历 s 和 t 的每一对字符。

5. 空间复杂度：

• 空间复杂度是 O(m * n)，因为我们需要一个二维的 DP 数组来存储中间结果。

class Solution {
    public boolean isSubsequence(String s, String t) {
        
        int[][] dp = new int[s.length()+1][t.length()+1];
        for(int i=1; i<s.length()+1; i++){
            for(int j=1; j<t.length()+1; j++){
                if(s.charAt(i-1) == t.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1]+1;
                }else{
                    dp[i][j] = dp[i][j-1];      //这里只“删”t的元素
                }
            }
        }
        return dp[s.length()][t.length()] == s.length() ? true : false;
    }
}