算法day37-动态规划（10）子序列系列

目录

1. 最长递增子序列
2. 最长连续递增子序列
3. 最长重复子数组

一、最长递增子序列

 https://leetcode.cn/problems/longest-increasing-subsequence/description/?envType=problem-list-v2&envId=8At1GmaZ

 

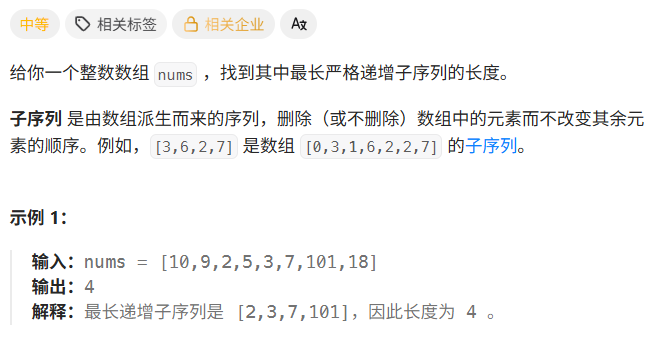
class Solution {
    public int lengthOfLIS(int[] nums) {//dp[i]:以nums[i]结尾的最长递增子序列的长度
        int[] dp = new int[nums.length];
        Arrays.fill(dp,1);
        int maxSize = 1;
        for(int i=1; i<nums.length; i++){
            for(int j=0; j<i; j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i], dp[j]+1);  
                }      
            }
            maxSize = Math.max(maxSize, dp[i]);
        }
        //return dp[nums.length-1];       //× 这不是我们最终的结果
        return maxSize;
    }
}

 

二、最长连续递增子序列

 https://leetcode.cn/problems/longest-continuous-increasing-subsequence/description/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        dp[0] = 1;
        int res = 1;
        for(int i=1; i<nums.length; i++){
            if(nums[i-1] < nums[i]){
                dp[i] = Math.max(dp[i], dp[i-1]+1);
            }
            res = Math.max(dp[i], res);
        }
        return res;
    }
}

 

三、最长重复子数组

 https://leetcode.cn/problems/maximum-length-of-repeated-subarray/description/?envType=problem-list-v2&envId=8At1GmaZ

 

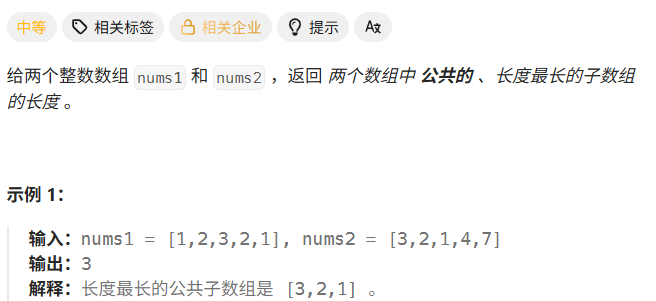
class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        //dp[i][j]：以nums1[i-1]为结尾、以nums2[j-1]为结尾的公共的 、长度最长的子数组的长度
        int res = 0;
        int[][] dp = new int[nums1.length+1][nums2.length+1];
        for(int i=1; i<nums1.length+1; i++){
            for(int j=1; j<nums2.length+1; j++){
                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1]+1;
                    res = Math.max(dp[i][j], res);
                }
            }
        }
        return res;
    }
}