算法day33-动态规划（6）

目录

1. 零钱兑换
2. 完全平方数
3. 单词拆分
4. 多重背包了解

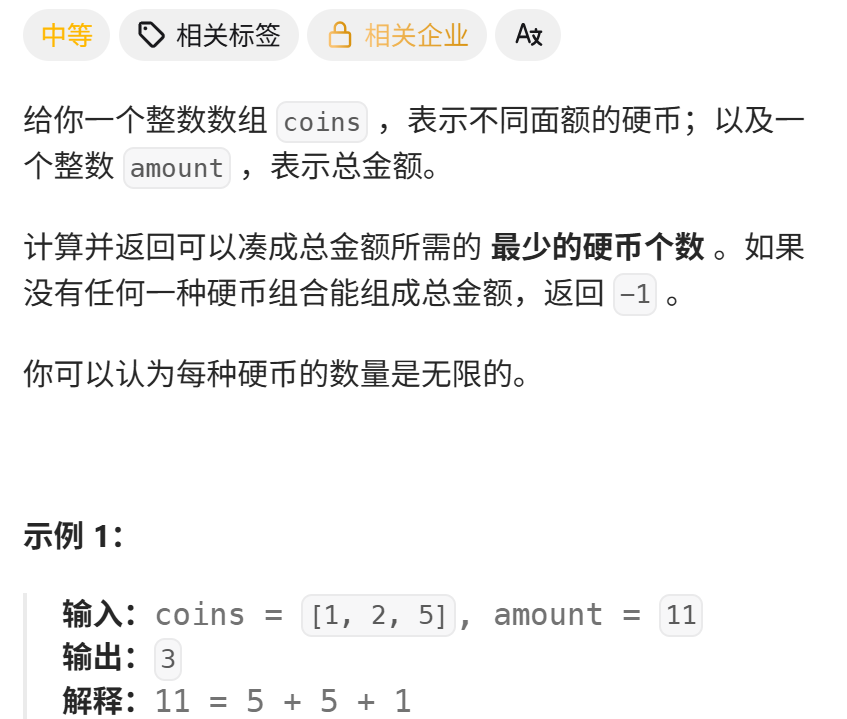
一、零钱兑换

 https://leetcode.cn/problems/coin-change/description/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int coinChange(int[] coins, int amount) {
        //dp[j]：装满容量为j的背包最少物品的数量
        int[] dp = new int[amount+1];
        int max = Integer.MAX_VALUE;
        Arrays.fill(dp, max);
        dp[0] = 0;
        for(int i=0; i<coins.length; i++){
            for(int j=coins[i]; j<=amount; j++){
                if(dp[j-coins[i]] != max){
                    dp[j] = Math.min(dp[j], dp[j-coins[i]]+1);
                }
            }
        }
        return dp[amount] == max ? -1 : dp[amount];
    }
}

 

📋 初始状态

定义：

• dp[j] 表示组成金额 j 的方法数

初始化：

dp[0] = 1 dp[1~5] = 0

---

🧮 逐个硬币处理：

我们一行一行模拟 dp[j] += dp[j - coins[i]] 的过程：

---

✅ 第一轮：使用硬币 1

for (j = 1; j <= 5): dp[j] += dp[j - 1]

j	0	1	2	3	4	5
dp[]	1	1	1	1	1	1

 

含义：所有金额都能由多个 1 元硬币凑出，方法数为 1

---

✅ 第二轮：使用硬币 2

for (j = 2; j <= 5): dp[j] += dp[j - 2]

j	0	1	2	3	4	5
dp[]	1	1	2	2	3	3

 

解释：

• dp[2] += dp[0] → 1 + 1 = 2

• dp[3] += dp[1] → 1 + 1 = 2

• dp[4] += dp[2] → 1 + 2 = 3

• dp[5] += dp[3] → 1 + 2 = 3

组合方式多了，如：

• 2+2, 1+1+2, 等等

---

✅ 第三轮：使用硬币 5

for (j = 5; j <= 5): dp[5] += dp[0]

j	0	1	2	3	4	5
dp[]	1	1	2	2	3	4

 

最终结果：

• dp[5] = 4，有四种组合方式可以凑出 5：

  1+1+1+1+1 1+1+1+2 1+2+2 5

二、完全平方数

 https://leetcode.cn/problems/perfect-squares/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int numSquares(int n) {
        //dp[j]:装满容量为j的背包的元素的最少数量
        int[] dp = new int[n+1];
        int max = Integer.MAX_VALUE;
        Arrays.fill(dp, max);
        dp[0] = 0;
        int[] nums = generateSquares(n);
        for(int i=0; i<nums.length; i++){
            for(int j=nums[i]; j<=n; j++){
                if(dp[j-nums[i]] != max){
                    dp[j] = Math.min(dp[j],dp[j-nums[i]]+1);
                }
            }
        }
        return dp[n];
    }

    // 生成所有 <= n 的完全平方数
    public int[] generateSquares(int n){
        List<Integer> list = new ArrayList<>();
        int i = 1;
        while(i * i <= n){
            list.add(i*i);
            i++;
        }
        // List<Integer> 转 int[]
        int[] res = new int[list.size()];
        for(int j=0; j<list.size(); j++){
            res[j] = list.get(j);
        }
        return res;
    }
}

 

三、单词拆分

 https://leetcode.cn/problems/word-break/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        //dp[i]:长度为i的字符串能否由字典组成
        boolean[] dp = new boolean[s.length()+1];
        for(int i=0; i<dp.length; i++){
            dp[i] = false;
        }
        dp[0] = true;
        for(int i=1; i<=s.length(); i++){
            for(int j=0; j<i; j++){
                String word = s.substring(j, i);
                if(wordDict.contains(word) && dp[j] == true){
                    dp[i] = true;
                }
            }
        }
        return dp[s.length()];
    }
}

 

四、多重背包了解