算法day32-动态规划（5）完全背包问题

目录

1. 完全背包理论
2. 零钱兑换II
3. 组合总和IV
4. 爬楼梯（进阶）

一、完全背包理论

 

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int bagWeight = scanner.nextInt();

        int[] weight = new int[n];
        int[] value = new int[n];

        for (int i = 0; i < n; i++) {
            weight[i] = scanner.nextInt();
            value[i] = scanner.nextInt();
        }

        int[][] dp = new int[n][bagWeight + 1];

        // 初始化
        for (int j = weight[0]; j <= bagWeight; j++) {
            dp[0][j] = dp[0][j - weight[0]] + value[0];
        }

        // 动态规划
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= bagWeight; j++) {
                if (j < weight[i]) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
                }
            }
        }

        System.out.println(dp[n - 1][bagWeight]);
        scanner.close();
    }
}

 

二、零钱兑换II——不强调顺序

 https://leetcode.cn/problems/coin-change-ii/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int change(int amount, int[] coins) {
        // dp[j]：装满容器为j的背包有多少种方法
        int[] dp = new int[amount+1];
        dp[0] = 1;          //背包容量为0只有一种方法
        for(int i=0; i<coins.length; i++){
            for(int j=coins[i]; j<=amount; j++){
                dp[j] += dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
}

-----------------------------------------
//目标和（0-1背包）

class Solution {

    public int findTargetSumWays(int[] nums, int target) {

        //求容量为target的背包有多少种装的方法

        int sum = 0;

        for(int x : nums){

            sum += x;

        }

        //left+right = sum

        //left-right = target

        //left = (sum+target)/2;

        if(Math.abs(target)>sum)    return 0;

        if((sum+target) % 2 == 1)   return 0;

        int bagSize = (sum+target)/2;

        int[] dp = new int[bagSize+1];

        dp[0] = 1;

        for(int i=0; i<nums.length; i++){

            for(int j=bagSize; j>=nums[i]; j--){

                dp[j] += dp[j-nums[i]];

            }

        }

        return dp[bagSize];

    }

}

 

三、组合总和IV——强调顺序

 https://leetcode.cn/problems/combination-sum-iv/description/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int combinationSum4(int[] nums, int target) {
        //dp[j]：容量为j的背包能装的物品组合有多少种
        int[] dp = new int[target+1];
        dp[0] = 1;
        //遍历背包
        for(int j=0; j<=target; j++){
            //遍历物品
            for(int i=0; i<nums.length; i++){
                if( j >= nums[i]){
                    dp[j] += dp[j-nums[i]];
                }
            }
        }
        return dp[target];
    }
}

 

四、爬楼梯（进阶）

 

 

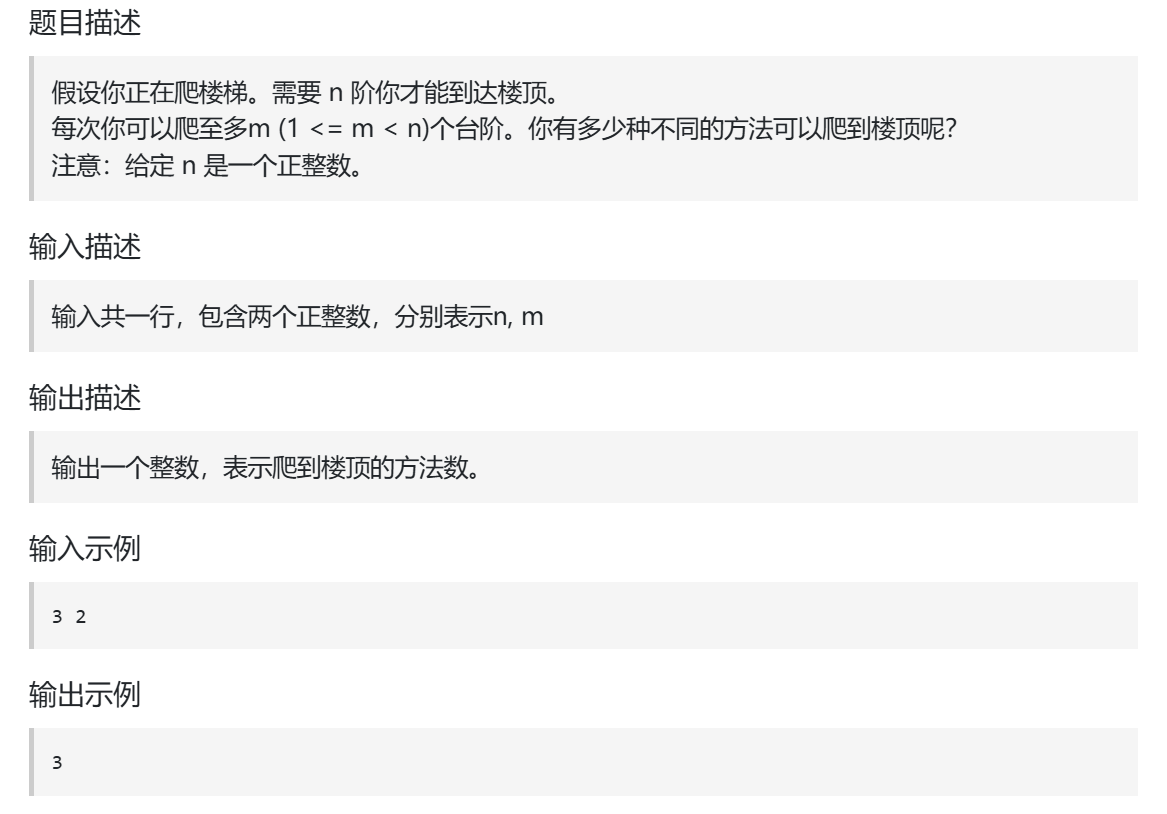
import java.util.Scanner;
class climbStairs{
    public static void main(String [] args){
        Scanner sc = new Scanner(System.in);
        int m, n;
        while (sc.hasNextInt()) {
            // 从键盘输入参数，中间用空格隔开
            n = sc.nextInt();
            m = sc.nextInt();

            // 求排列问题，先遍历背包再遍历物品
            int[] dp = new int[n + 1];
            dp[0] = 1;
            for (int j = 1; j <= n; j++) {
                for (int i = 1; i <= m; i++) {
                    if (j - i >= 0) dp[j] += dp[j - i];
                }
            }
            System.out.println(dp[n]);
        }
    }
}

------------------------------------------------------------
//斐波那契数做法
class Solution {
    public int climbStairs(int n) {
        //1.确定dp数组的含义：dp[i]，达到第i层有多少种方法
        //2.确定递推公式：dp[i] = dp[i-1]+dp[i-2];
        //3.初始化
        if(n == 1){
            return n;
        }
        int[] dp = new int[n+1];
        dp[1] = 1;
        dp[2] = 2;
        for(int i=3; i<=n; i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
}