算法day29-动态规划（2）

目录

1. 不同路径
2. 不同路径II
3. 整数拆分
4. 不同的二叉搜索树

一、不同路径

https://leetcode.cn/problems/unique-paths/description/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int uniquePaths(int m, int n) {
        //1.dp[i][j]：到达(i,j)这个位置这么多条路径
        //2.dp[i][j] = dp[i-1][j] + dp[i][j-1];
        //3.初始化
        int[][] dp = new int[m+1][n+1];
        for(int i=0; i<n; i++){
            dp[0][i] = 1;           //到第一列的格子只有一种走法：从左边来
        } 
        for(int i=0; i<m; i++){
            dp[i][0] = 1;           //到第一列的格子只有一种走法：从右边来
        }
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

 

二、不同路径II

https://leetcode.cn/problems/unique-paths-ii/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        //1.dp[i][j]：表示到达(i,j)这个点的不同路径数量
        //2.dp[i][j] = dp[i-1][j] + d[i][j-1];      //注意障碍物
        //3.初始化
        int[][] dp = new int[m][n];

        //判断起点或终点是不是障碍
        if(obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1){
            return 0;
        }
        dp[0][0] = 1;
        for(int i=1; i<n; i++){
            if(obstacleGrid[0][i] != 1){        //如果这个点不是障碍
                dp[0][i] = 1;
            }else{
                break;
            }
        }
        for(int i=1; i<m; i++){
            if(obstacleGrid[i][0] != 1){        //如果这个点不是障碍
                dp[i][0] = 1;
            }else{
                break;
            }
        }
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                if(obstacleGrid[i][j] != 1){
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
}

 

三、整数拆分

https://leetcode.cn/problems/integer-break/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    public int integerBreak(int n) {
        //1.dp[i]：正整数i的最大乘积
        //2.dp[i] = 
        int[] dp = new int[n+1];
        dp[2] = 1;
        for(int i=3; i<=n; i++){
            for(int j=1; j<=i/2; j++){      //表示从j开始拆分,i/2是优化
                dp[i] = Math.max(dp[i],Math.max(j*(i-j), j*dp[i-j]));
            }
        }
        return dp[n];
    }
}

 

四、不同的二叉搜索树

https://leetcode.cn/problems/unique-binary-search-trees/?envType=problem-list-v2&envId=8At1GmaZ

 

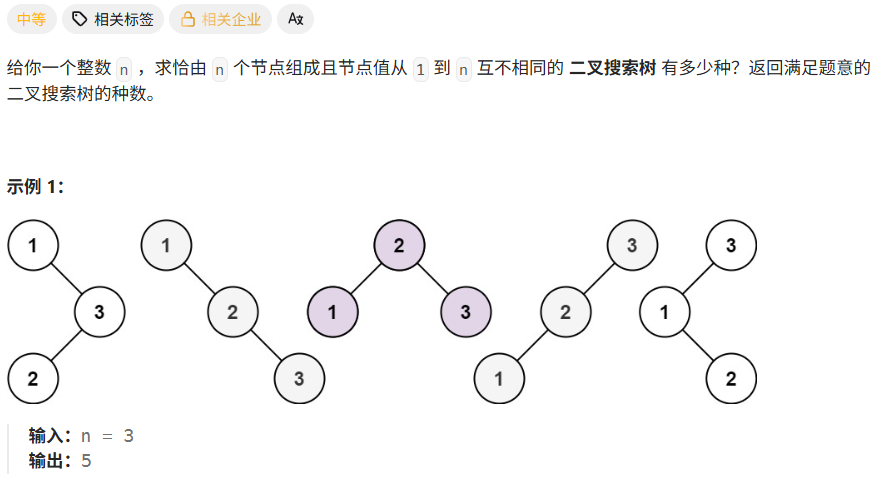
class Solution {
    public int numTrees(int n) {
        //dp[i]:i个节点可以组成的二叉搜索树的个数
        int[] dp = new int[n+1];
        dp[0] = 1;      //表示空节点有1种二叉搜索树的形式
        for(int i=1; i<=n; i++){            //遍历从1-n的数字
            for(int j=1; j<=i; j++){            //固定根节点的值是j，遍历每个数当根节点的情况
                dp[i] += dp[j-1] * dp[i-j];         //左节点有多少种*右节点有多少种
            }
        }
        return dp[n];
    }
}