算法day19-回溯（1）

目录

1. 理论基础
2. 组合
3. 组合总和III
4. 电话号码的字母组合

一、理论基础

 　　回溯法，一般可以解决以下问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符按一定规则有几种切割方式
• 子集问题：一个N个数的集合里面有多少符合条件的子集
• 排列问题：N个数按照一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等

　　组合无序，排列有序！

　　回溯法解决的问题都可以抽象为树形结构，因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。递归就要有终止条件，所以必然是一棵高度有限的树。

 

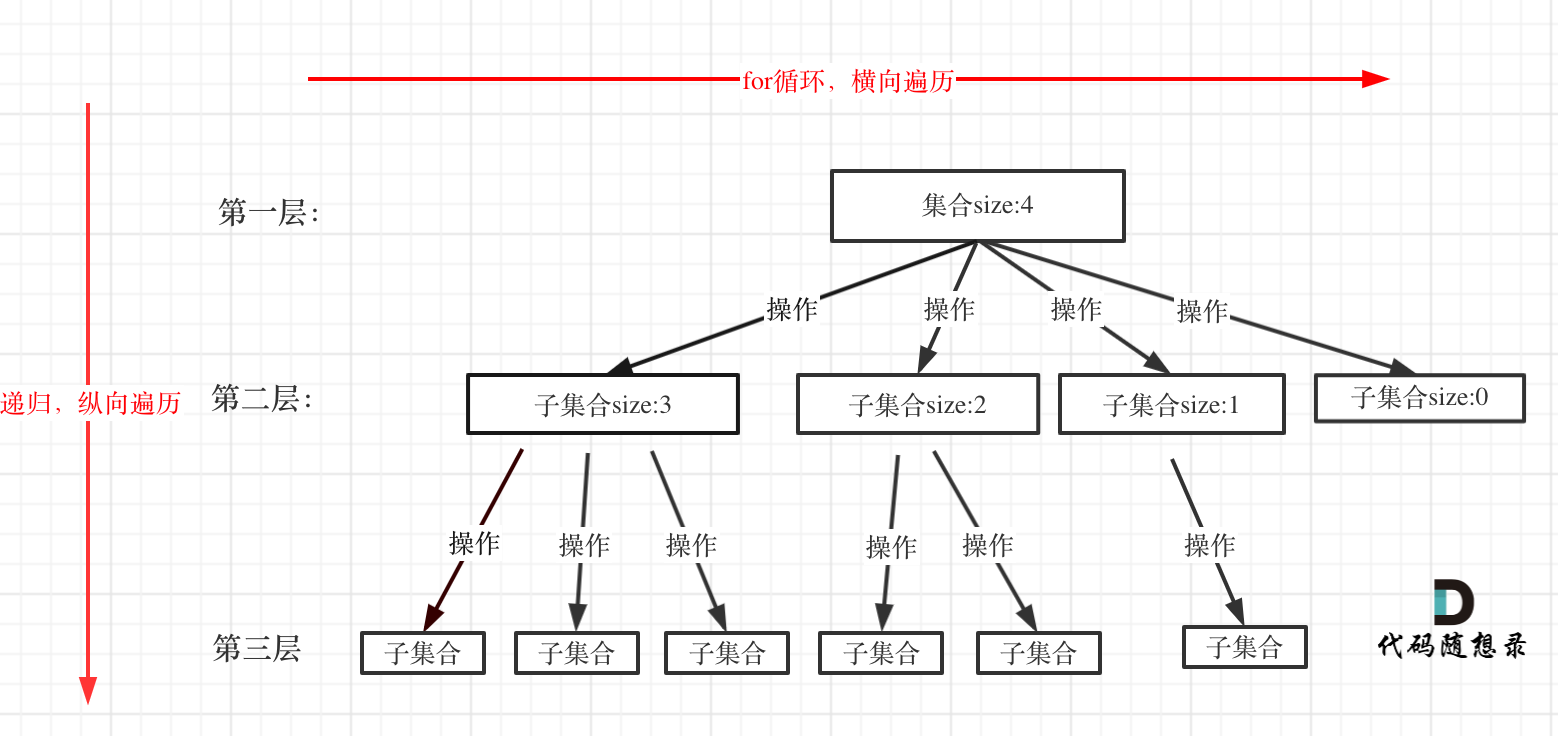
　　回溯法模板：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

二、组合_【组合问题】

 https://leetcode.cn/problems/combinations/description/?envType=problem-list-v2&envId=8At1GmaZ

class Solution {
    List<List<Integer>> res;
    List<Integer> path;
    public List<List<Integer>> combine(int n, int k) {
        res = new ArrayList<>();
        path = new ArrayList<>();
        dfs(1,k,n);      //入口
        return res;
    }
    public void dfs(int i,int k, int n){
        if(path.size() == k){       //终止条件:树的深度到k
            res.add(new ArrayList<>(path));
            return;
        }
        for(int j=i; j<=n; j++){
            path.add(j);
            dfs(j+1, k,n);
            path.remove(path.size()-1);
        }
    }
}

三、组合总和III

 https://leetcode.cn/problems/combination-sum-iii/description/?envType=problem-list-v2&envId=8At1GmaZ

class Solution {
    List<List<Integer>> res;
    List<Integer> path;
    public List<List<Integer>> combinationSum3(int k, int n) {
        res = new ArrayList<>();
        path = new ArrayList<>();
        dfs(1, k, n, 0);
        return res;
    }
    public void dfs(int i, int k, int n,int sum){
        if(path.size() == k){       //必须要用k个数
            if(sum == n){
                res.add(new ArrayList<>(path));
            }
            return;
        }
        if(sum > n){
            return;     //剪枝
        }
        for(int j=i; j<=9; j++){
            path.add(j);
            dfs(j+1, k, n, sum+j);
            path.remove(path.size()-1);
        }
    }
}

 

四、电话号码的字母组合

 https://leetcode.cn/problems/letter-combinations-of-a-phone-number/?envType=problem-list-v2&envId=8At1GmaZ

 

class Solution {
    List<String> res = new ArrayList<>();
    String path = "";
    public List<String> letterCombinations(String digits) {
        if(digits == null || digits.length() == 0){
            return res;
        }
        String[] nums = new String[10];
        nums[2] = "abc";
        nums[3] = "def";
        nums[4] = "ghi";
        nums[5] = "jkl";
        nums[6] = "mno";
        nums[7] = "pqrs";
        nums[8] = "tuv";
        nums[9] = "wxyz";
        dfs(0, digits, nums);

        return res;
    }

    public void dfs(int i, String digits, String[] nums){ // i 是第几个号码
        if(i == digits.length()){
            res.add(path);
            return;
        }
        // 把 i 对应的号码取出来
        int idx = digits.charAt(i) - '0';
        for(char d : nums[idx].toCharArray()){
            path = path + d;
            dfs(i + 1, digits, nums);
            path = path.substring(0, path.length() - 1);
        }

    }
}

 

 

引用：https://programmercarl.com/%E5%9B%9E%E6%BA%AF%E7%AE%97%E6%B3%95%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html#%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80