算法day17-二叉树（7）

目录

1. 二叉搜索树的最近公共祖先
2. 二叉搜索树中的插入操作
3. 删除二叉搜索树中的节点

一、二叉搜索树的最近公共祖先

 https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/description/?envType=problem-list-v2&envId=8At1GmaZ

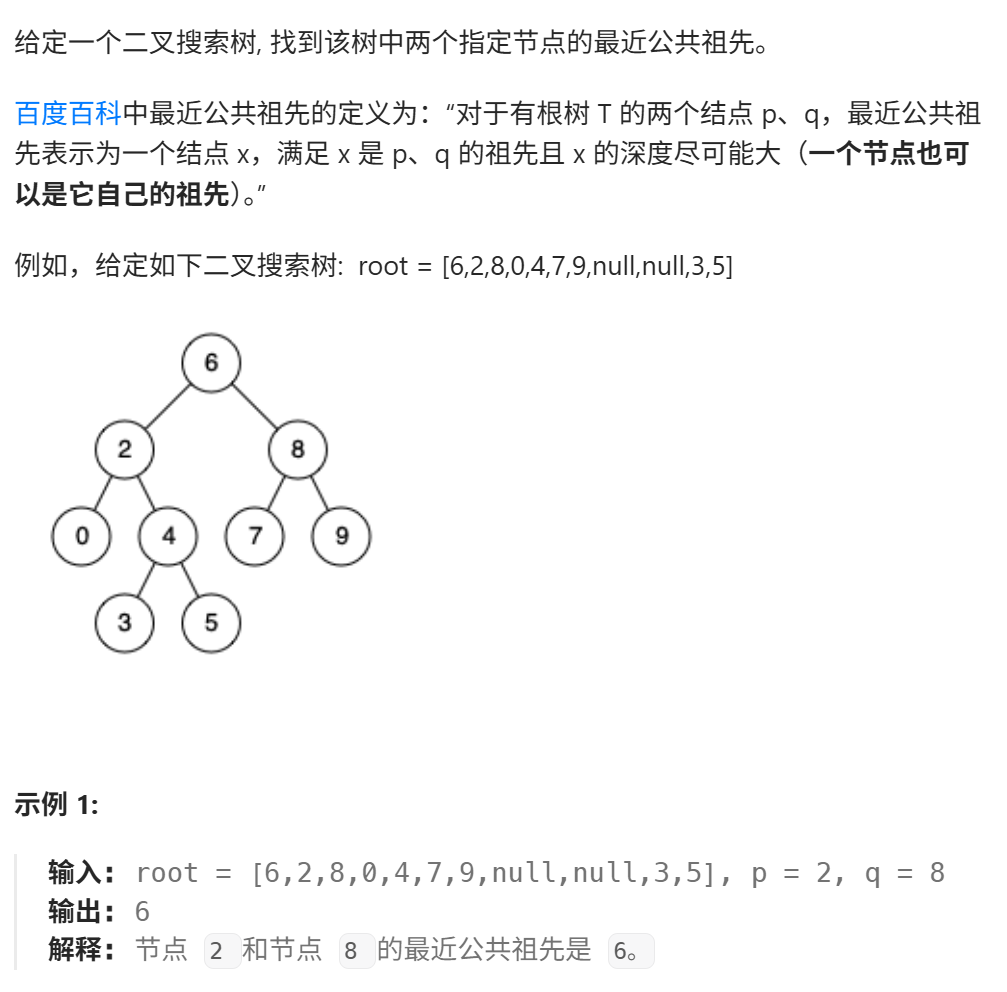
　　方法一：

class Solution {
    TreeNode res = new TreeNode(-1);
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null){
            return null;
        }
        // System.out.print(res == null);
        int x = p.val, y = q.val;
        if(x > y){
            int temp = x;
            x = y;
            y = temp;
        }
        findAncestor(root, x, y);
        return res;
    }

    public void findAncestor(TreeNode root, int x, int y){
        if(res.val != -1){
            return;
        }
        if(root.val >= x && root.val <= y){
            //返回答案
            // System.out.println("find" + " " +root.val);
            res = root;
            return;
        }
        if(root.val > x && root.val > y ){
            findAncestor(root.left, x, y);   
        }else if(root.val < x && root.val < y){
            findAncestor(root.right, x, y);  
        }
    }
}

　　方法二：非递归。

class Solution{
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while((long)(root.val - p.val) * (root.val - q.val) > 0){
            root = p.val < root.val ? root.left : root.right;
        }
        return root;
    }  
}

二、二叉搜索树中的插入操作

 https://leetcode.cn/problems/insert-into-a-binary-search-tree/?envType=problem-list-v2&envId=8At1GmaZ

 

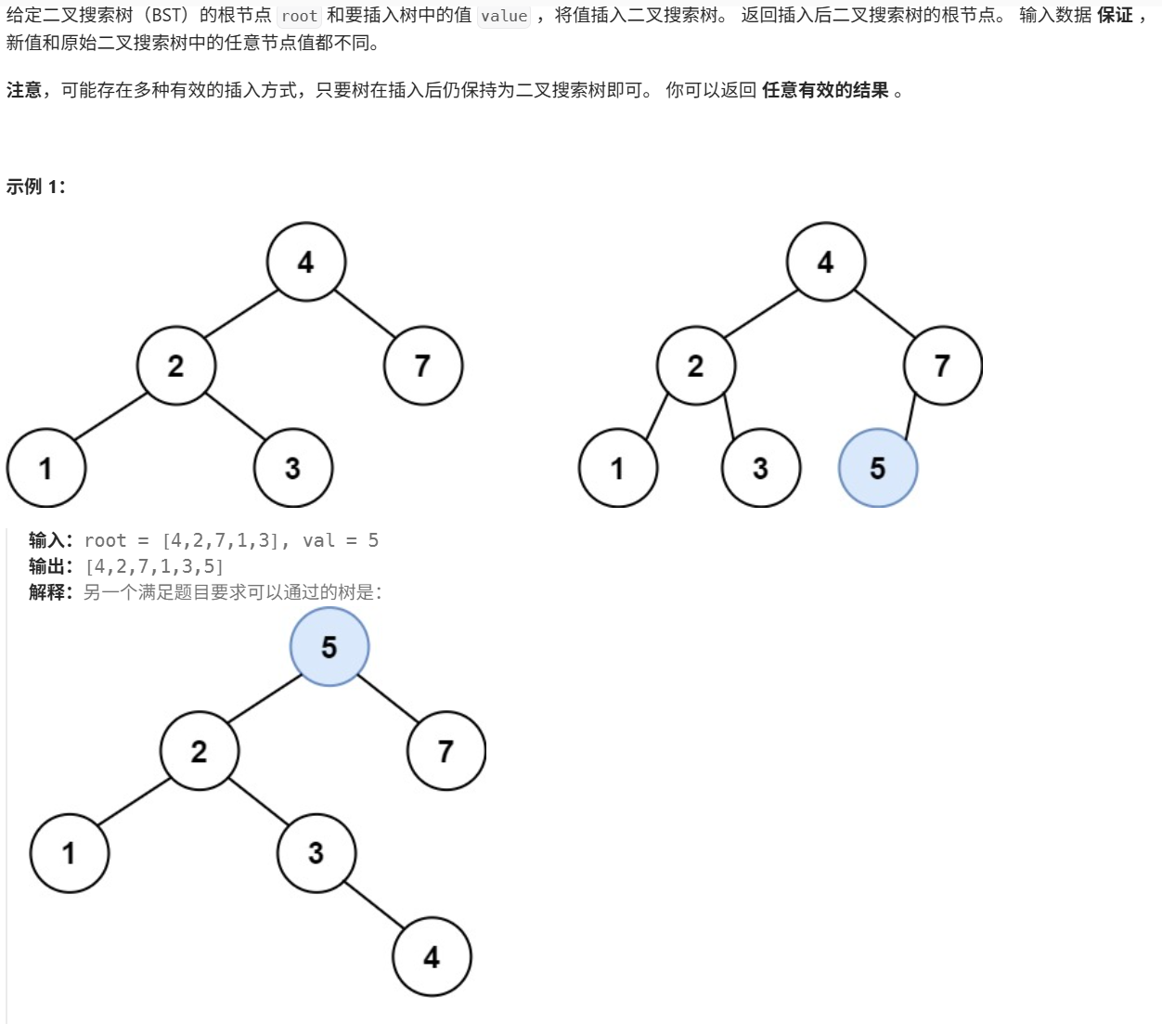
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if(root == null) return new TreeNode(val);
        TreeNode node = root;
        while(true){
            if(node.val < val){
                if(node.right == null){
                    node.right = new TreeNode(val);
                    break;
                }else{
                    node = node.right;
                }
            }else{
                if(node.left == null){
                    node.left = new TreeNode(val);
                    break;
                }else{
                    node = node.left;
                }
            }
        }
        return root;
    }
}

 

三、删除二叉搜索树中的节点

https://leetcode.cn/problems/delete-node-in-a-bst/?envType=problem-list-v2&envId=8At1GmaZ

 

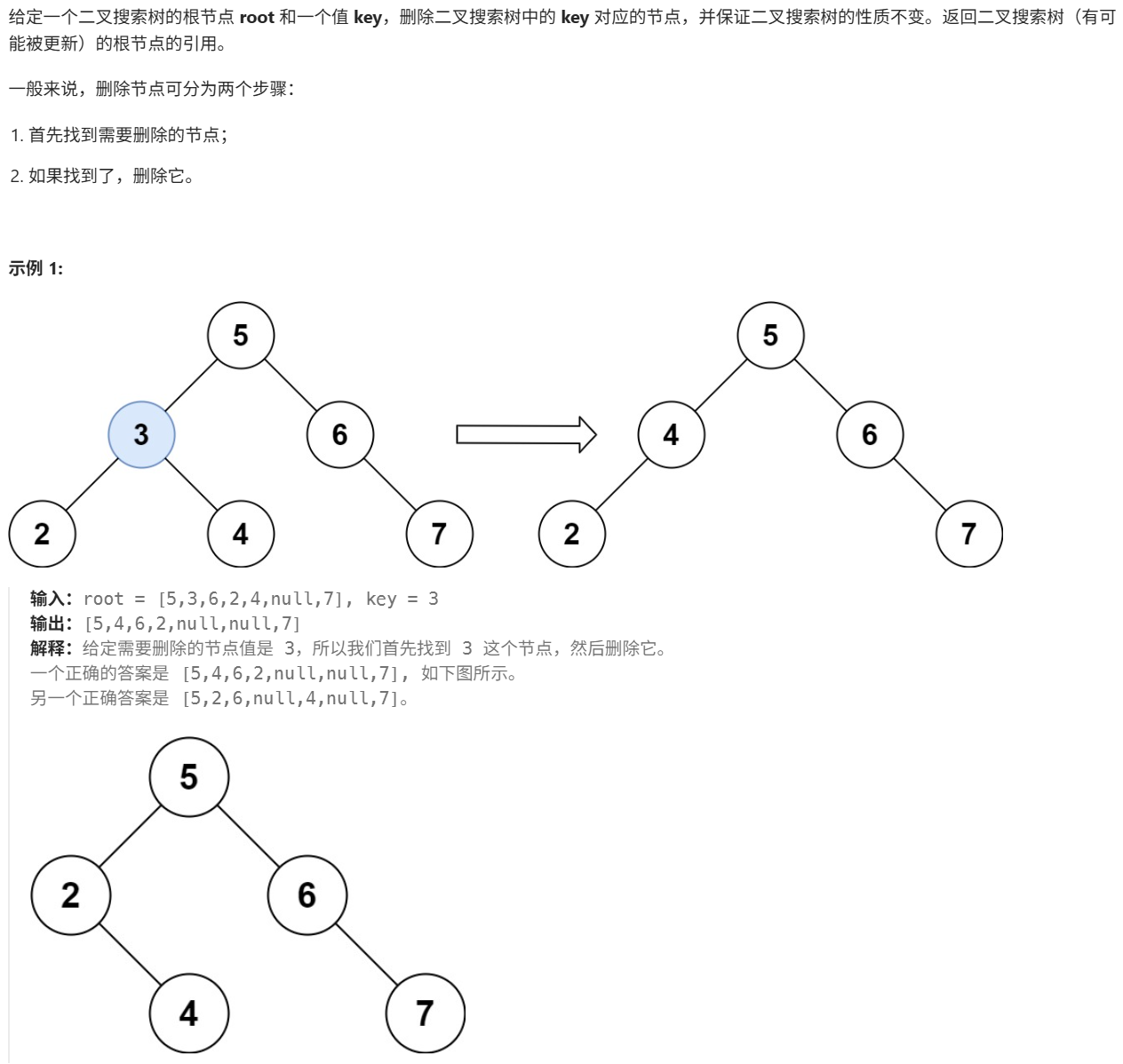
class Solution{
    if(root == null)    return null;
        if(key > root.val){
            root.right = deleteNode(root.right, key);
        }else if(key < root.val){
            root.left = deleteNode(root.left, key);
        }else{
            if(root.left == null)   return root.right;
            else if(root.right == null)  return root.left;
            else if(root.left != null && root.right != null){
                TreeNode node = root.right;     //保存当前节点的右子树
                while(node.left != null){
                    node = node.left;           //寻找要删除的节点右子树的最左节点
                }
                node.left = root.left;      // 将欲删除节点的左子树成为其右子树的最左节点的左子树
                root = root.right;      //欲删除节点的右子顶替其位置，节点被删除
            }
        }
        return root;
    }
}