算法day11-二叉树（1）

目录

1. 二叉树理论基础
2. 二叉树递归遍历
3. 二叉树迭代遍历
4. 统一的迭代遍历方法
5. 小结

一、二叉树理论基础

　　种类：满二叉树（除了叶子节点外，每个节点都有两个子节点）、完全二叉树（每一层都被填满，最后一层从左到右连续排列）、二叉搜索树（左子树所有节点小于根节点，右子树所有节点大于根节点）、平衡二叉搜索树（在 BST 基础上增加了高度平衡限制，使查找效率更优）。

　　存储方式：

• 1）顺序存储：用数组来存储。若父节点的数组下标是i，那么左孩子就是i*2+1，右孩子就是i*2+2。
• 2）链式存储：

class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int val){
         this.val = val;      
    }
};

• 3）遍历方法：
  • 深度优先遍历：前序（递归、迭代）、中序（递归、迭代）、后序（递归、迭代）
  • 广度优先遍历：层序遍历（迭代法）

二、二叉树递归遍历

 　　写递归函数的三个步骤：

• 确定参数和返回值
• 写清终止条件：加个”停止递归“的判断，不然会无限调用导致程序崩溃。
• 写好每一层要干啥

 1. 二叉树的前序遍历（根 → 左 → 右）

　　前序遍历是按照：根-左-右的顺序来访问。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        preorder(root, res);
        return res;
    }

    public void preorder(TreeNode root, List<Integer> res){
        if(root == null){
            return;
        }
        res.add(root.val);
        preorder(root.left, res);
        preorder(root.right, res);
    }
}
//时间复杂度：O（n），其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
//空间复杂度：O（n），平均情况为O（logn），最坏情况为O（n）

 2. 二叉树的中序遍历（左 → 根 → 右）

　　适用于二叉搜索树，遍历结果是有序数组。

class Solution{
    public List<Integer> inorderTraversal(TreeNode root){
        List<Integer> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }

    public void inorder(TreeNode root, List<Integer> res){
        if(root == null){
            return;
        }
        inorder(root.left, res);
        res.add(root.val);
        inorder(root.right, res);
    }
}

 3. 二叉树的后序遍历（左 → 右 → 根）

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        postorder(root, res);
        return res;
    }

    public void postorder(TreeNode root, List<Integer> res){
        if(root == null){
            return;
        }
        postorder(root.left, res);
        postorder(root.right, res);
        res.add(root.val);
    }
}

三、二叉树迭代遍历

　　迭代遍历主要使用 栈（Stack）来模拟递归过程，使得程序更具显式流程。

 1. 二叉树的前序遍历

• 使用栈先处理左子树。

• 每次访问当前节点后，将右子节点入栈，保证左子节点优先出栈。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        while(!stack.isEmpty() || node != null){
            while(node != null){
                res.add(node.val);
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            node = node.right;
        }
        return res;
    }
}
//时间复杂度：O(n)
//空间复杂度：O(n)

 2. 二叉树的中序遍历

• 使用栈一直向左深入，直到最左叶子。

• 退栈访问当前节点，再右移。

class Solution{
    public List<Integer> inorderTraversal(TreeNode root){
        List<Integer> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        while(!stack.isEmpty() || node!=null){
            while(node != null){
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            res.add(node.val);
            node = node.right;
        }
        return res;
    }
}

 3. 二叉树的后序遍历

• 较为复杂，需记录“上一次访问的节点”prev，判断右子树是否处理过。

• 若右子树尚未处理，需要先压栈等待右子树遍历完成。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode prev = null;
        while(root != null || !stack.isEmpty()){
            //先处理左边的所有节点（相对）
            while(root != null){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();     //从栈里弹出来一个
            if(root.right == null || root.right == prev){       //如果右边没有节点或右边节点已被处理过
                res.add(root.val);
                prev = root;        //记录上一个处理过的节点
                root = null;        //这里主要是控制不用处理左边节点了
            }else{
                stack.push(root);       //处理右边的节点
                root = root.right;
            }
        }
        return res;
    }
}
//时间复杂度：O（n）
//空间复杂度：O（n） 

四、二叉树层序遍历

　　层序遍历采用 队列（Queue） 实现，属于 广度优先搜索（BFS）。

• 每一层入队一次，遍历队列中所有节点，将其子节点依次加入队列。

• 可以通过 level.size() 控制当前层级的节点数量，确保按层处理。

　　　这个方法特别适合：求层数、最短路径；按层收集结果；广度相关题目（如最小深度、右视图等）。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            List<Integer> level = new ArrayList<>();
            int size = queue.size();
            for(int i=0; i<size; i++){
                TreeNode cur = queue.poll();
                level.add(cur.val);
                if(cur.left != null)    queue.offer(cur.left);
                if(cur.right != null)   queue.offer(cur.right);
            }
            res.add(level);
        }
        return res;
    }
}

 【扩展题】二叉树的层序遍历II（https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/description/?envType=problem-list-v2&envId=8At1GmaZ）

 

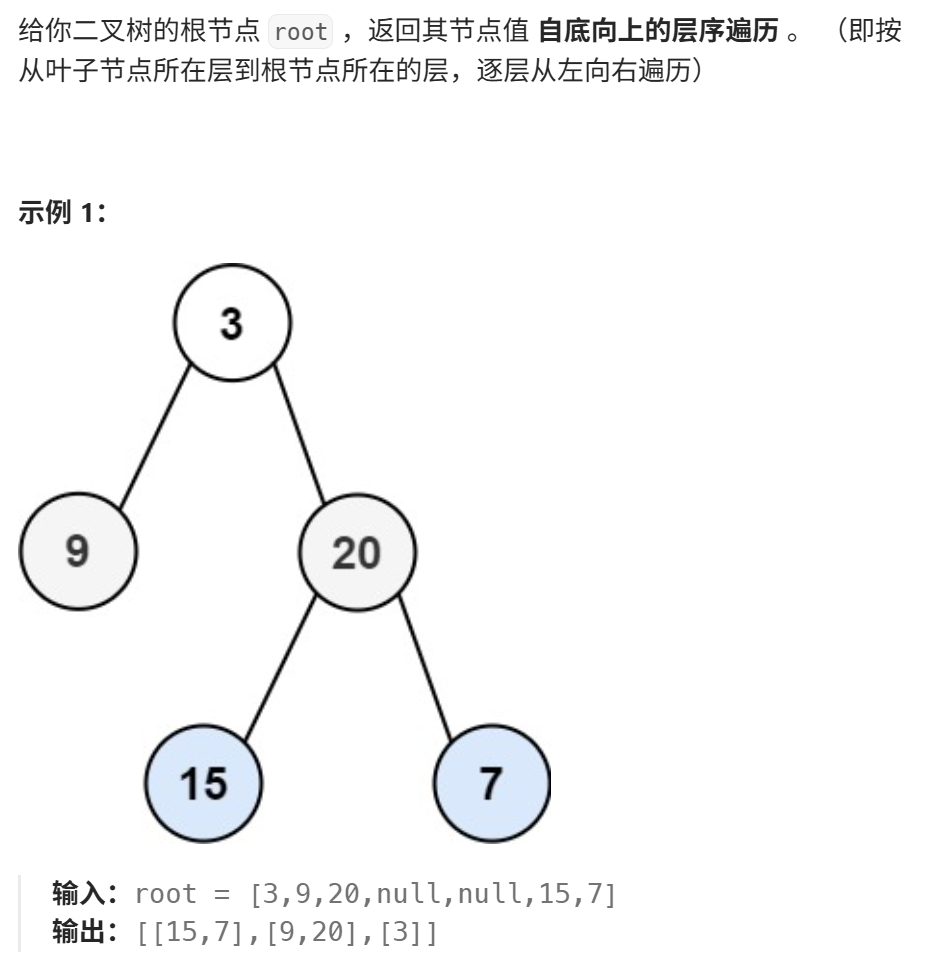
class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> res = new LinkedList<>();
        if(root == null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            List<Integer> level = new ArrayList<>();
            int size = queue.size();
            for(int i=0; i<size; i++){
                TreeNode cur = queue.poll();
                level.add(cur.val);
                if(cur.left!=null)  queue.offer(cur.left);
                if(cur.right!=null) queue.offer(cur.right);
            }
            res.add(0, level);      //在索引为0的位置插入
        }
        return res;
    }
}

 

参考

https://blog.csdn.net/qq_70244454/article/details/127748607