拉格朗日对偶函数
对偶函数
优化问题的形式
注意原问题不一定凸
\[\min f_0(x)\\
\begin{align*}
s.t. \ &f_i(x) \le 0 \quad &i=1,2,\cdots,m\\
&h_i(x)=0 \quad &i=1,2,\cdots,p
\end{align*}
\]
拉格朗日函数形式
\[L(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^m \lambda_i f_i(x)+\sum_{i=1}^p \nu_i h_i(x)
\]
对偶函数的定义
\[g(\lambda,\nu)=\inf_{x \in D}(f_0(x)+\sum_{i=1}^m \lambda_i f_i(x)+\sum_{i=1}^p \nu_i h_i(x))
\]
根据对偶函数的定义可知，对偶函数是拉格朗日函数在把\(\lambda\)和\(\nu\)当做常量，\(x\)变化时的最小值
注意：对偶问题则是
\[\max_{\lambda,\nu}g(\lambda,\nu)
\]
这里要着重说一下：对偶函数和对偶问题的区别
它们是非常不一样的概念，问题是为了求最值，而函数就是个f
对偶函数的性质
对偶函数一定是凹函数
逐点上确界 pointwise supremum
如果对于\(\forall y \in A,f(x,y)\)关于\(x\)是凸函数,那么函数\(g(x)=\sup_{y \in A} f(x,y)\)关于\(x\)是凸函数
同理,一组凹函数逐点下确界是凹函数
数学证明可以看这个博客
大概的思路就是对偶函数中最小化之后\(x\)已经是个定值，此时对偶函数\(g(\lambda,\nu)\)是相对于变量\(\lambda,\nu\)的一簇仿射函数，仿射函数是既凹又凸的，那么就利用其凹性，一簇仿射函数的下界就是一个凹函数。
也可以从下图直观的看出：
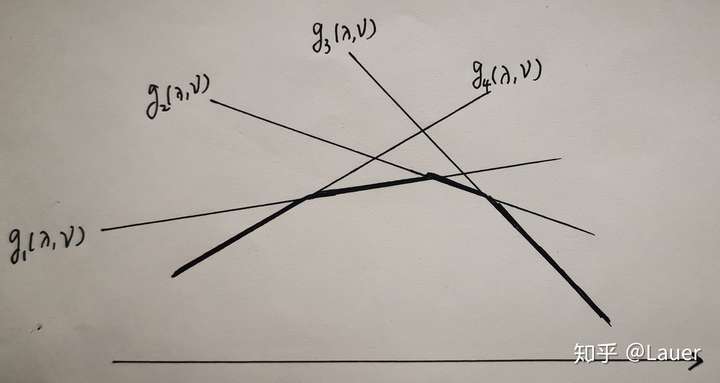
对偶函数的最优解$\le$原函数最优解
\[\forall \lambda_i \succeq 0,\forall \nu \quad g(\lambda,\nu) \le P^*
\]
一定要有\(\lambda_i \succeq 0\)这个条件
即对偶函数求得的函数值是原问题最优值的下界
这里再强调一遍：不等式左边是函数，不等式右边是问题的最优值
很好证明，因为
\[\begin{align*}
&\sum_{i=1}^m \lambda_i f_i(x^*)+\sum_{i=1}^p \nu_i h_i(x^*) \le 0, \quad 其中x为原问题最优解\\
&f_0(x^*)=P^*\\
\therefore \quad
&L(x^*,\lambda,\nu)=f_0(x^*)+\sum_{i=1}^m \lambda_i f_i(x^*)+\sum_{i=1}^p \nu_i h_i(x^*) \le P^*\\
\therefore \quad
&g(\lambda,\nu) \le P^*
\end{align*}
\]
对偶问题
再看一次对偶问题
\[\begin{align*}
\max_{\lambda,\nu}g(\lambda,\nu)=&\max_{\lambda,\nu}\min_{x}L(x,\lambda,\nu)\\
=&\max_{\lambda,\nu} f_0(x)+\sum_{i=1}^k \lambda f_i(x)+\sum_{i=1}^l \nu h_i(x)\\
\end{align*}
\]
对偶函数是从拉格朗日函数转换过来的，只跟\(\lambda,\nu\)相关的函数，不是一个问题（不需要得到最值什么的）
对偶问题利用对偶函数一定\(\le\)原问题最优解的性质,进而去求解对偶函数的最大值\(D^*\),将原问题通过对偶函数（凹函数）转化为求解对偶问题（凸优化问题）
为什么费尽周折的去转化成对偶问题呢？
因为无论原问题是否为凸优化问题，转化成的对偶问题一定是凸优化问题
为什么要转化成凸优化问题就不必多说了，具体可看凸优化问题的特性：局部最优解必是全局最优解
相关链接：拉格朗日对偶问题
