二分查找

我们知道二分查找的基础写法有三种：

1. 左闭右闭区间

    public static int binsearch(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while (l <= r) {
            int m = (l + r) / 2;
            if (nums[m] == target) return m;
            if (nums[m] > target) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }
}

因为这是一个闭区间，l和r都能取到，当区间只有一个数的时候，如[1]，l是可以等于r的，所以这里判断是l <= r。
2. 左闭右开区间

    public static int binsearch(int[] nums, int target) {
        int l = 0, r = nums.length;
        while (l < r) {
            int m = (l + r) / 2;
            if (nums[m] == target) return m;
            if (nums[m] > target) {
                r = m;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }

这边因为右边是开区间，r是取不到的，所以r的初始值是nums.length，而且因为r是取不到的，缩小右边区间是只需要让r = m。
3. 左开右开区间

    public static int binsearch(int[] nums, int target) {
        int l = -1, r = nums.length;
        while (l < r) {
            int m = (l + r) / 2;
            if (nums[m] == target) return m;
            if (nums[m] > target) {
                r = m;
            } else {
                l = m;
            }
        }
        return -1;
    }

这里两边都是开区间，l初始值得是-1，r初始值是nums.length，同样的缩小区间是l和r直接等于m。
上面的只是基础，如果涉及到一个数组中有相同的几个值，你是无法确定选出来的目标是哪一个，如果需要找出最左边的那个位置，应该怎么写？
这里主要是要确定如果中间的值正好等于target需要怎样舍弃哪一部分。
如果要找最左边的那个值，在nums等于target是应该让r缩小。看下面例子：

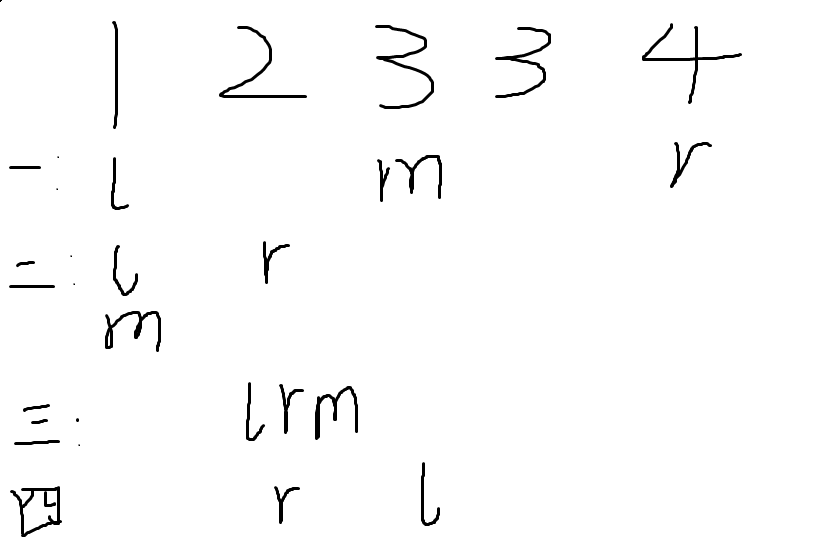
可以看到最终l就停留在了最左边的3。

    public static int binsearch(int[] nums, int target) {
        int l = 0, r = nums.length-1;
        while (l <= r) {
            int m = (l + r) / 2;
            if (nums[m] >= target) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return l;
    }

相识的，如果我要得到最右边的3，我只需要改变相等情况下的区间修改。

    public static int binsearch(int[] nums, int target) {
        int l = 0, r = nums.length-1;
        while (l <= r) {
            int m = (l + r) / 2;
            if (nums[m] > target) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return r;
    }

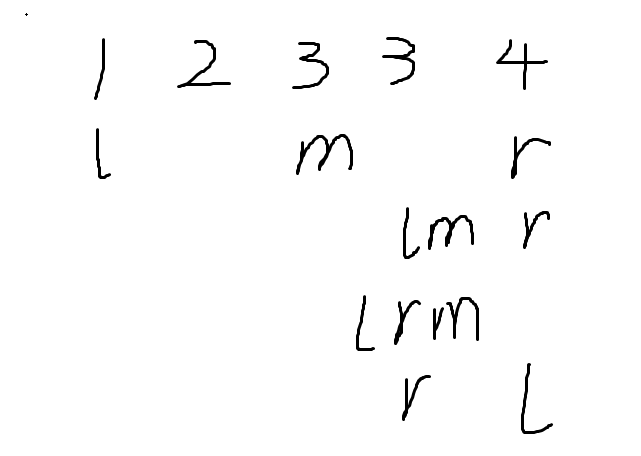
这里返回是r。