梯度下降学习笔记

0x01 梯度下降的算法思想

梯度下降（Gradient Descent）是一种通用的优化算法，能够为大范围的问题找到最优解。梯度下降的核心思想就是通过沿着目标函数的梯度负方向不断迭代更新参数从而使目标函数最小化。该算法被广泛应用于机器学习和 AI 中。

若将目标函数视为一个超曲面，梯度下降的过程即为从曲面上的某一点出发，沿着坡度最陡的下坡方向一步步移动，直到接近最低点。

假设目标函数为 \(J(\theta)\)，其中 \(\theta=(\theta_1, \theta_2, \dots, \theta_n)\) 是待优化的参数组成的向量。首先，梯度下降使用一个按一定规则初始化的 \(\theta\) 值，然后逐步改进，每次走出一步，尝试降低一点 \(J(\theta)\) 的值，直到算法收敛。

0x02 参数更新过程

梯度 \(\nabla_\theta J(\theta)\) 是一个向量，其每个分量为函数对相应参数的偏导数，即：

\[\nabla_\theta J(\theta)=\left(\frac{\partial J(\theta)}{\partial \theta_1},\frac{\partial J(\theta)}{\partial\theta_2},\dots, \frac{\partial J(\theta)}{\partial \theta_n} \right) \]

梯度的方向表示函数在该点增长最快的方向，而梯度的负方向则是函数值下降最快的方向。在每次迭代中，参数按如下公式更新：

\[\theta_{t+1}=\theta_t-\eta\cdot\nabla_\theta \]

其中：

• \(\theta_t\) 是第 \(t\) 次迭代后的参数值。
• \(\eta\) 是学习率（Learning Rate），控制每次更新的步长。

若学习率过低，算法要经过大量迭代才能收敛，耗费大量时间。

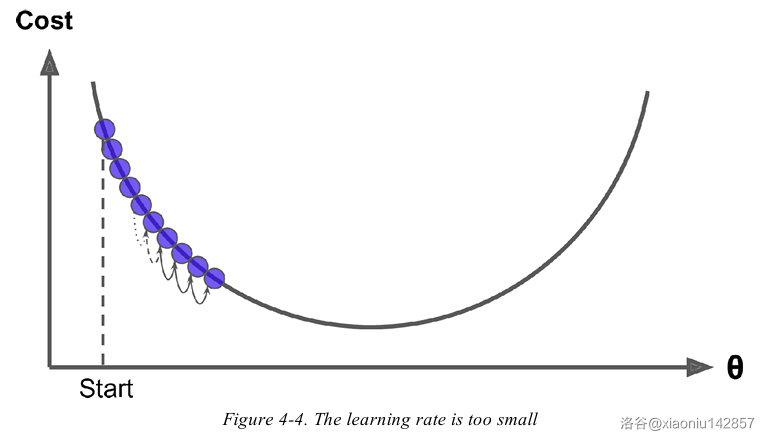
若学习率过高，算法可能直接越过极小值，会导致算法震荡或发散。

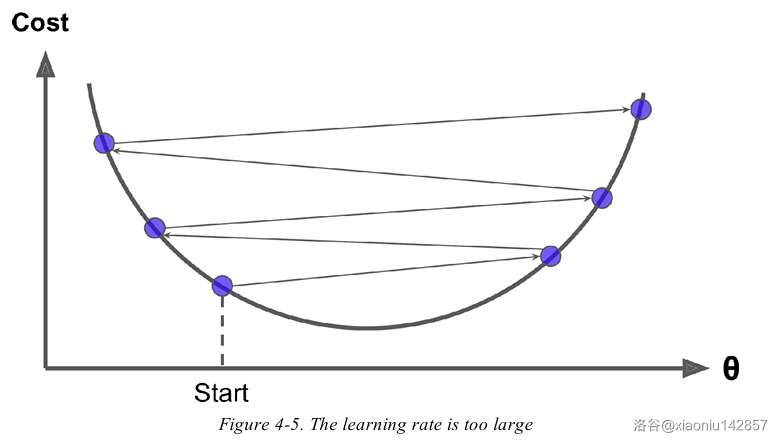
并不是所有目标函数都是碗状的。有些函数的形状可能会导致算法很难找到最小值。如果从下图的左边出发会陷入局部极小值。从右侧出发则会经过很长时间才能穿越整片高原。

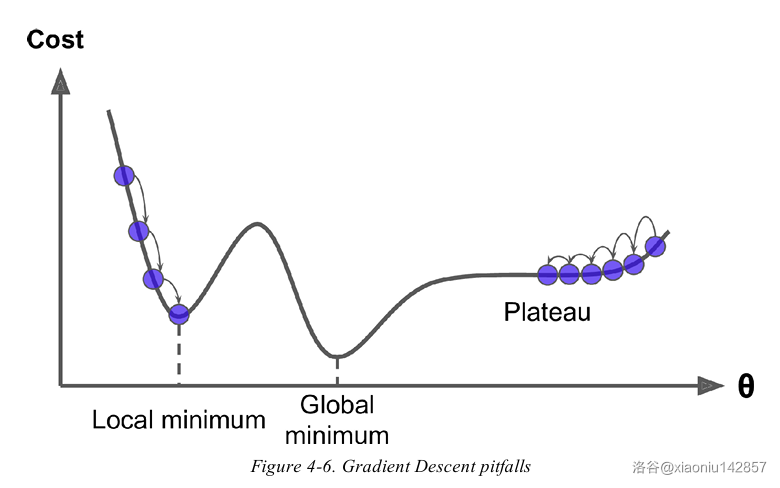
0x03 梯度下降的分类

在机器学习中，根据每次迭代使用的样本量，梯度下降可分为三类：

类型	定义与特点	优缺点
批量梯度下降（BGD）	每次迭代使用全部训练数据计算梯度，更新参数。	收敛方向稳定，但数据量庞大时计算成本高，迭代速度慢。
随机梯度下降（SGD）	每次迭代仅使用一个样本计算梯度，更新参数。	计算效率高，更新频繁但方向随机性大，可能震荡或在最小值附近波动，但具有随机性，有助于跳出局部最小值。
小批量梯度下降（MBGD）	每次迭代使用一小批样本计算梯度，更新参数。	结合 BGD 和 SGD 的优点，既保证收敛稳定性，又提高计算效率，实际中最常用。

0x04 例题：P1337 [JSOI2004] 平衡点 / 吊打XXX

题目大意

给定平面上 \(n\) 个点，求它们的带权费马点。即求一个绳结所在点 \((x,y)\) 使得 \(\sum_{i=1}^n w_i\sqrt{(x_i-x)^2+(y_i-y)^2}\)（绳结位置到所有点的加权欧拉距离之和）最小。这一点可以参考其他题解的物理分析，这里就不再赘述。

Solution

这道题明明是裸的梯度下降呀！参数向量 \(\theta\) 即为绳结坐标 \((x,y)\)，目标函数 \(J(x,y)=\sum_{i=1}^n w_i\sqrt{(x_i-x)^2+(y_i-y)^2}\)（上面的柿子）。先画个图看一下每一项。

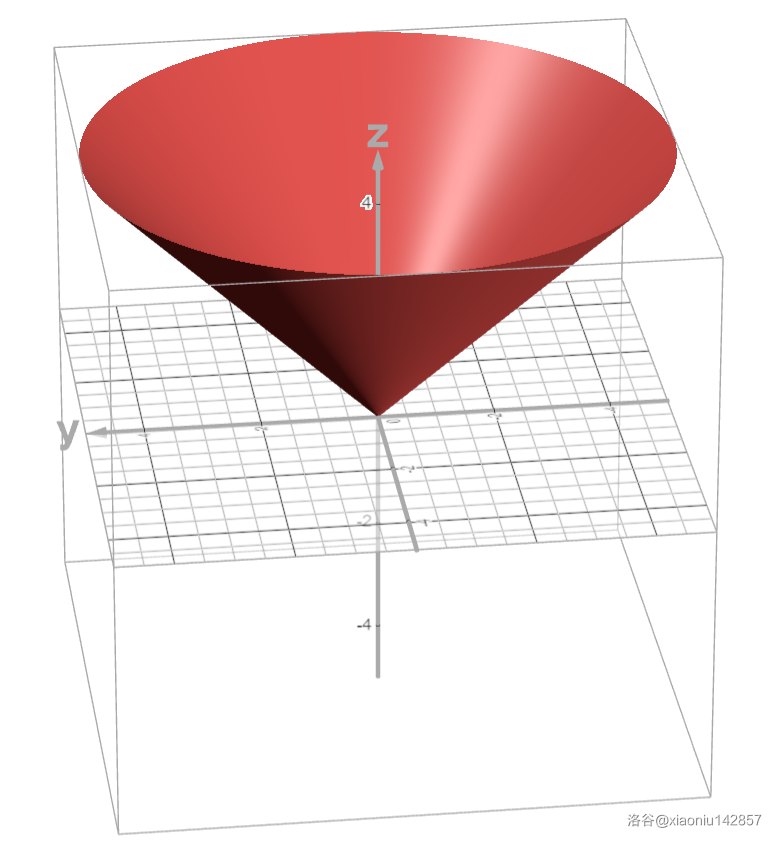
它是一个倒立的圆锥，是单谷函数。因此整个目标函数也是单谷函数，梯度下降保证收敛到全局最小值。注意到，该函数在极小值处不可导，因此应该忽略这样的不可导项。

求出偏导数：

\[\frac{\partial J(x,y)}{\partial x}=\sum_{i=1}^n w_i \cdot\frac{x-x_i}{\sqrt{(x-x_i)^2+(y-y_i)^2}} \\ \frac{\partial J(x,y)}{\partial y}=\sum_{i=1}^n w_i \cdot\frac{y-y_i}{\sqrt{(x-x_i)^2+(y-y_i)^2}} \]

最后，我们需要在算法执行过程中动态调整学习率来达到较好的效果，这被称为学习率调度。这里采用如下方式进行学习率调度：设 \(\eta_t\) 为第 \(t\) 次迭代后的学习率，则 \(\eta_{t+1}=r\cdot\eta_t\)，其中 \(0<r<1\)，为学习率衰减因子，而初始学习率 \(\eta_0\) 为定值。不断迭代直到 \(\eta<eps\) 或 \(|\nabla_\theta J(\theta)|<eps\)（即梯度向量的长度小于 \(eps\)）。这样一开始利用了较大学习率收敛快的优点，执行到后面学习率逐渐减小，有助与提高精度，收敛到极小值。这样很好地平衡了不同学习率的优缺点。

Code

这里取 \(\eta_0=100,r=0.99,eps=10^{-6}\)。

#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;
constexpr int N=1005;
constexpr double LR=100.0,DECAY=0.99,EPS=1e-6;  // 梯度下降超参数：初始学习率、衰减因子、精度
double x[N],y[N],w[N];
int n;
pair<double,double> gradient(double curX,double curY){  // 计算梯度
    pair<double,double> grad={0.0,0.0};
    for(int i=0;i<n;++i){
        double dx=curX-x[i];
        double dy=curY-y[i];
        double dist=sqrt(dx*dx+dy*dy);
        if(dist<EPS) continue;  // 避免除零错误
        grad.first+=w[i]*dx/dist;
        grad.second+=w[i]*dy/dist;
    }
    return grad;
}
int main(){
    cin.tie(0)->sync_with_stdio(0);
    double curX=0.0,curY=0.0,sumW=0.0,lr=LR;
    cin>>n;
    for(int i=0;i<n;++i){
        cin>>x[i]>>y[i]>>w[i];
        curX+=x[i],curY+=y[i],sumW+=w[i];
    }
    curX/=sumW,curY/=sumW;  // 初始化为所有点加权平均位置（玄学优化）
    while(lr>EPS){
        pair<double,double> grad=gradient(curX,curY);  // 计算梯度向量
        double gradLen=sqrt(grad.first*grad.first+grad.second*grad.second);  // 梯度向量的长度
        if(gradLen<EPS) break;  // 梯度足够小，已收敛
        curX-=lr*grad.first;
        curY-=lr*grad.second;
        lr*=DECAY;  // 学习率调度
    }
    cout<<fixed<<setprecision(3)<<curX<<' '<<curY;
    return 0;
}

Update 2025.6.16：修改一处公式错误。