还是老规矩,这一篇博客是对SVM进行介绍,下一篇博客就是使用SVM进行具体的使用。
SVM介绍
首先介绍SVM是什么,SVM(support vector machine)名为支持向量机,又名支持向量网络,是一个非常经典且高效的分类模型,是一种监督式的学习方法。
从名字上面来理解,SVM分为两个部分,"支持向量(support vector)"以及“机(machine)”。“machine”很简单的理解,就是算法的意思,那么“support vector”是什么呢? 这个现在不进行介绍,待我慢慢的引入。
线性分类
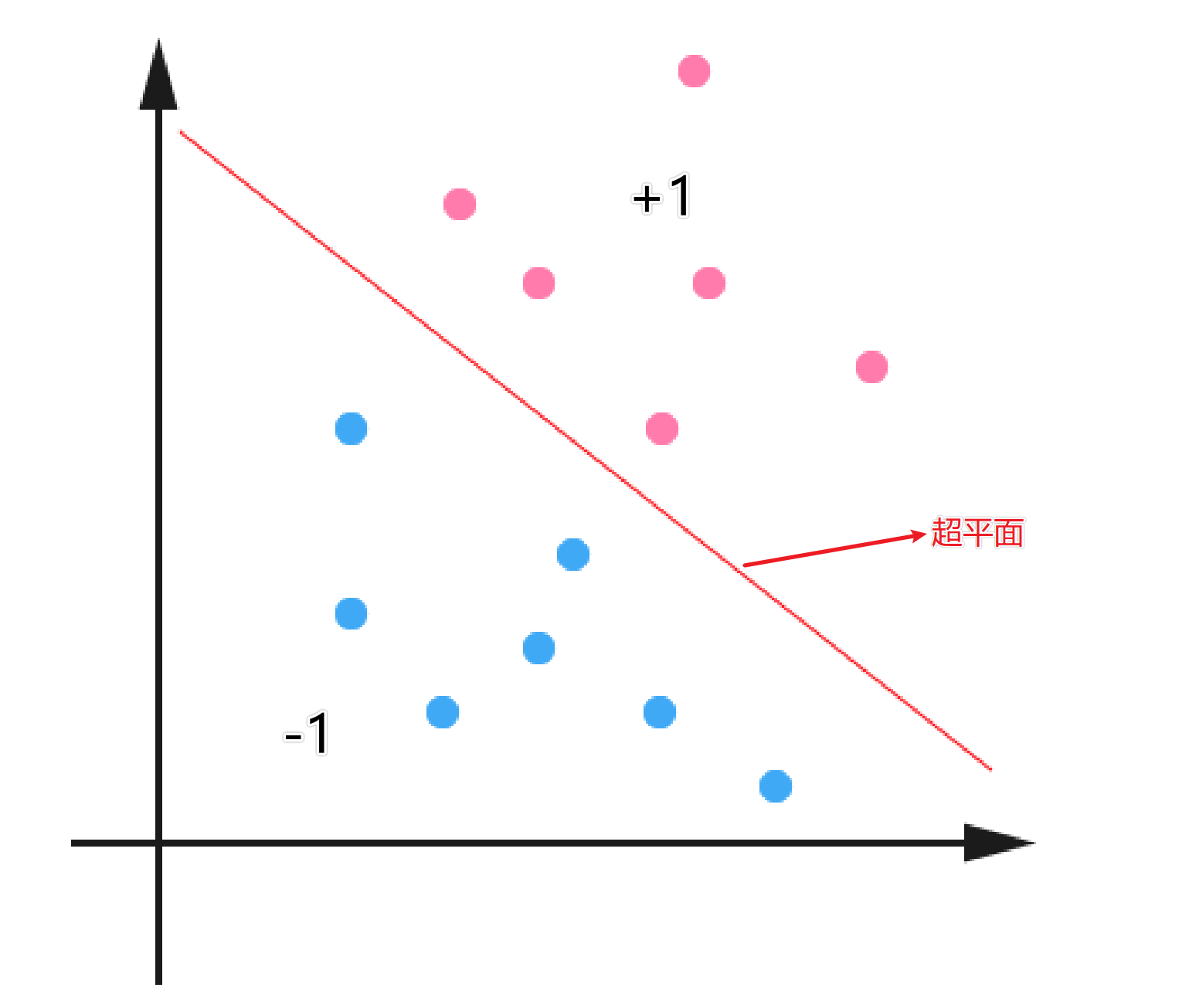
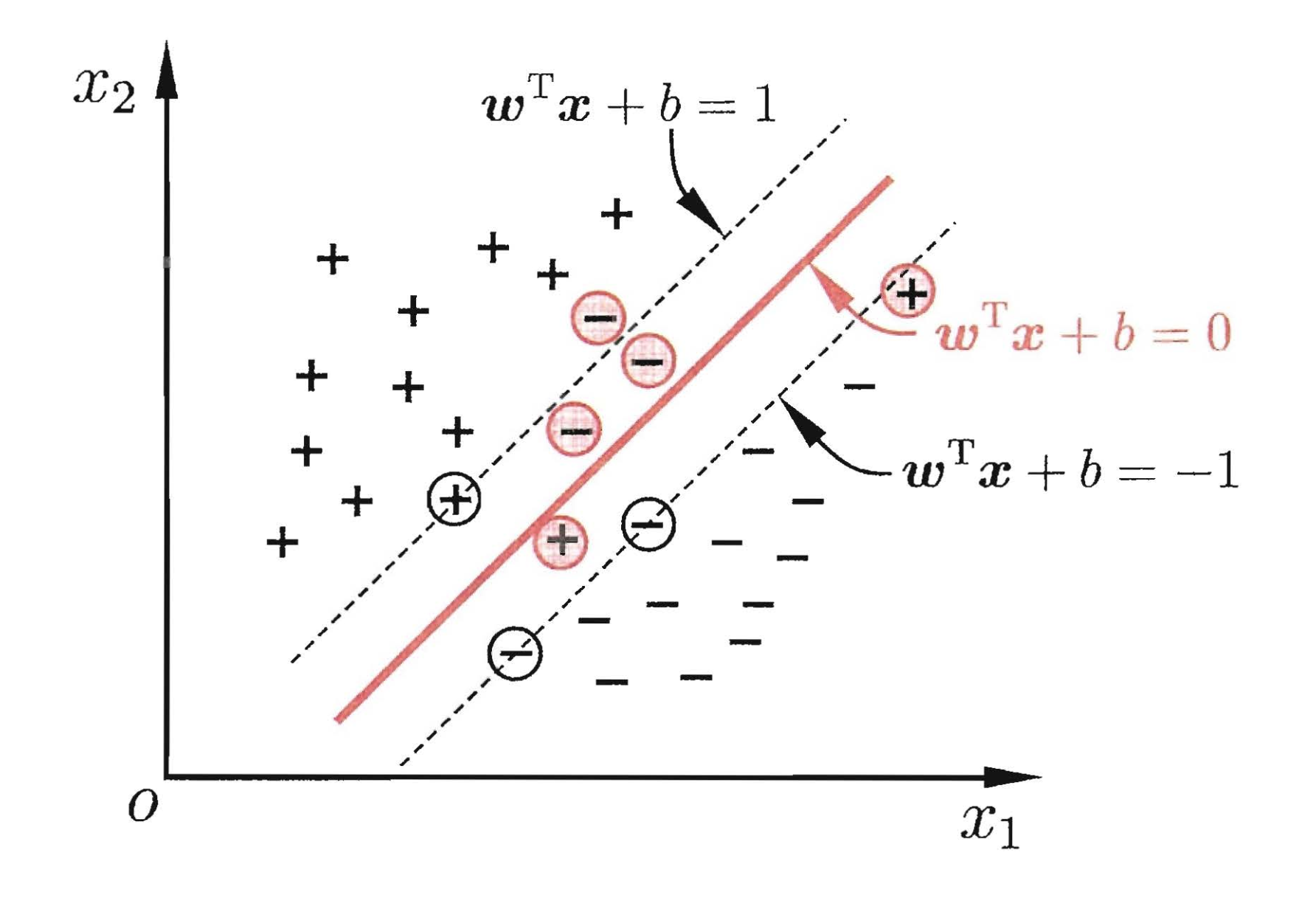
在介绍SVM之前,我们得先对线性分类器进行介绍。下面是一个二维平面的的分类问题,红色代表类别为+1,蓝色的代表类别是-1。中间的线就代表分割这两类问题的超平面。对于分类问题来说,红色和蓝色的点都是数据集中已知的,而我们的目的就是找到一个最适合的超平面,将数据进行分类。
对于线性二分类模型,给定一组数据\(\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, y_{m}\right)\right\}\), 其中\(\boldsymbol{x}_{i} \in \mathbb{R}^{d}, y \in\{-1,1\}\),二分类任务的目标是希望从数据中学得一个假设函数\(h: \mathbb{R} \rightarrow\{-1,1\}\),使得\(h(x_i) = y_i\)
\[\begin{equation}
h\left(\boldsymbol{x}_{i}\right)=\left\{\begin{array}{ll}
1 & 若 y_{i}=1 \\
-1 & 若 y_{i}=-1\\\tag{1}
\end{array}\right.
\end{equation}
\]
那么问题来了,我们如何去寻找一个能够将\(y_i = \pm1\)划分开的超平面?首先我们可以设超平面的函数是:
\[\begin{equation}f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\end{equation} \tag{2}
\]
这里有一个值得注意的点,下面的这个公式会在后面的推导中经常用到。
\[y_i^2 = 1 \tag{3}
\]
尽管有很多的问题都是线性不可分的,但是呢,目前我们只讨论线性可分问题,到后面我们再讨论如何将非线性问题转成线性问题。因此,暂时我们不需要去纠结如果是非线性问题怎么办。
我们可以直观的从图中进行感受,这样的超平面是有多个的,那么如何寻找一个最合适的超平面呢(也就是寻找最合适的\(w^{\mathrm{T}}\) 和\(b\))?接下来引出间隔的概念来寻找最合适的超平面。
间隔
如下图所示,超平面\(\begin{equation}f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\end{equation}\),则\(x\)为\(x_0\)到超平面的投影,\(x_0\)对应的类别是\(y_0\),\(w\)为超平面的法向量,\(\gamma\)为\(x_0\)到超平面的距离(带正负号)。
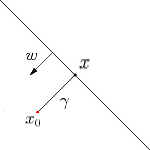
因此
\[\begin{aligned}
& \gamma = \frac{f(x_0)}{||w||} \\
& 因此距离(不带正负号)的为: \\
& \tilde{\gamma} = y_0\gamma
\end{aligned}
\]
这样我们就推出了间隔的表达式\(\tilde{\gamma} = y_0\gamma\)。对于给定的数据集,我们当然是希望数据集中的数据离超平面越远越好,因为这样所能够容忍的误差也就越大。那么这个远如何来确定呢?接下来让我们讨论什么是最大间隔分类器。
最大间隔分类器
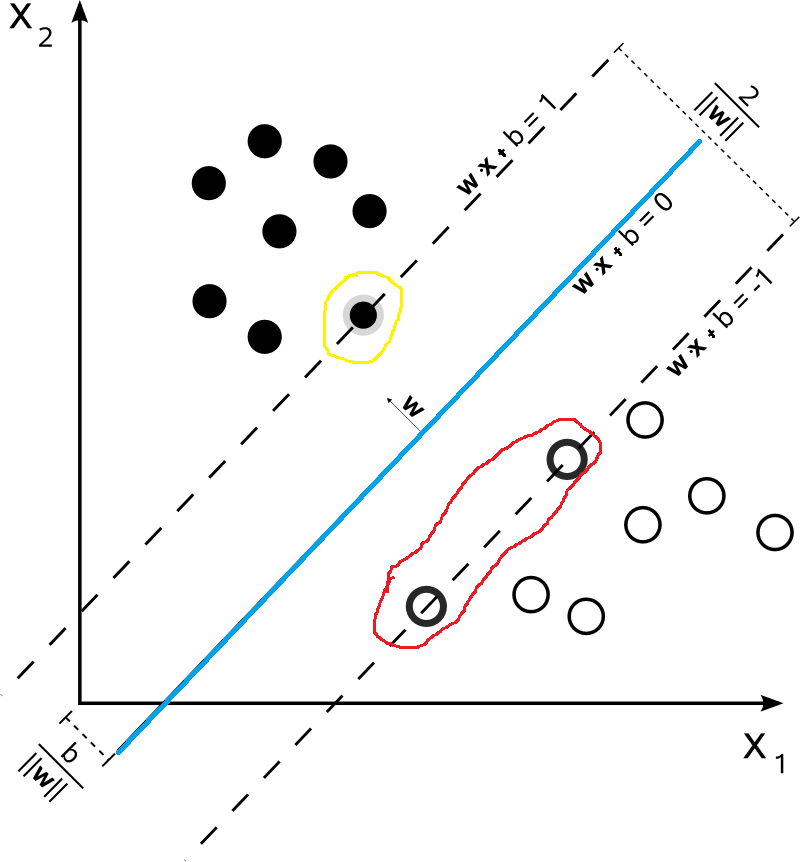
如果我们给定如下的数据集,那么对于下面的数据集,哪一些最不可能分类成功呢?毋庸置疑的,就是最靠近\(\begin{equation}f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\end{equation}\)超平面的数据点(比如下图中被红色和黄色圈出来的点)。而被圈出来的点也就是被称之为“支持向量”。因为在模型中我们考虑他们就可以了。
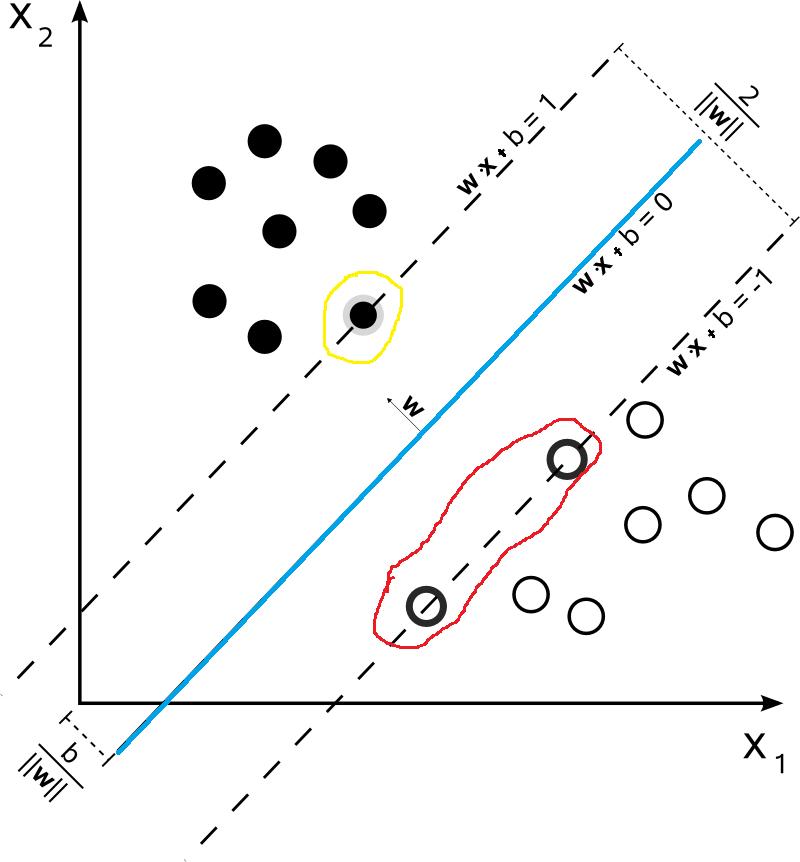
首先我们假设支持向量分布在\(\omega^Tx+b=\pm 1\)超平面上,这里取值为1只是为了方便,该值并不影响后面的优化结果。很显然,支持向量到超平面\(\omega^Tx+b=\pm 1\)的距离为\(\frac{1}{\|\omega\|}\)。两侧的距离加起来就是\(\frac{2}{\|\omega\|}\)。在前面我们说过,我们希望距离越大越好,也就是说\(\frac{2}{\|\omega\|}\)越大越好,同时对于数据集中数据的分布满足\(y(\omega^T+b)x \geqslant 1\)。因此,我们得到了如下的优化问题:
\[\left \{ \begin{matrix} \begin{align*}
& \max \quad \frac{2}{\Vert \omega \Vert} \\
& s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m
\end{align*} \end{matrix} \right.
\tag{4}
\]
为了方便后续的推导,该优化问题等价于:
\[\left \{ \begin{matrix} \begin{align*}
& \min \quad \frac{1}{2}\| \omega \|^2 \\
& s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m
\end{align*} \end{matrix} \right.
\tag{5}
\]
拉格朗日乘子法(Lagrange multipliers)
拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法。通过引拉格朗日乘子,可将有 \(d\)个变量与\(k\)个约束条件的最优化问题转化为具有\(d+k\)个变量的无约束优化问题求解。下面让我们来进行推导。
拉格朗日乘子法推导
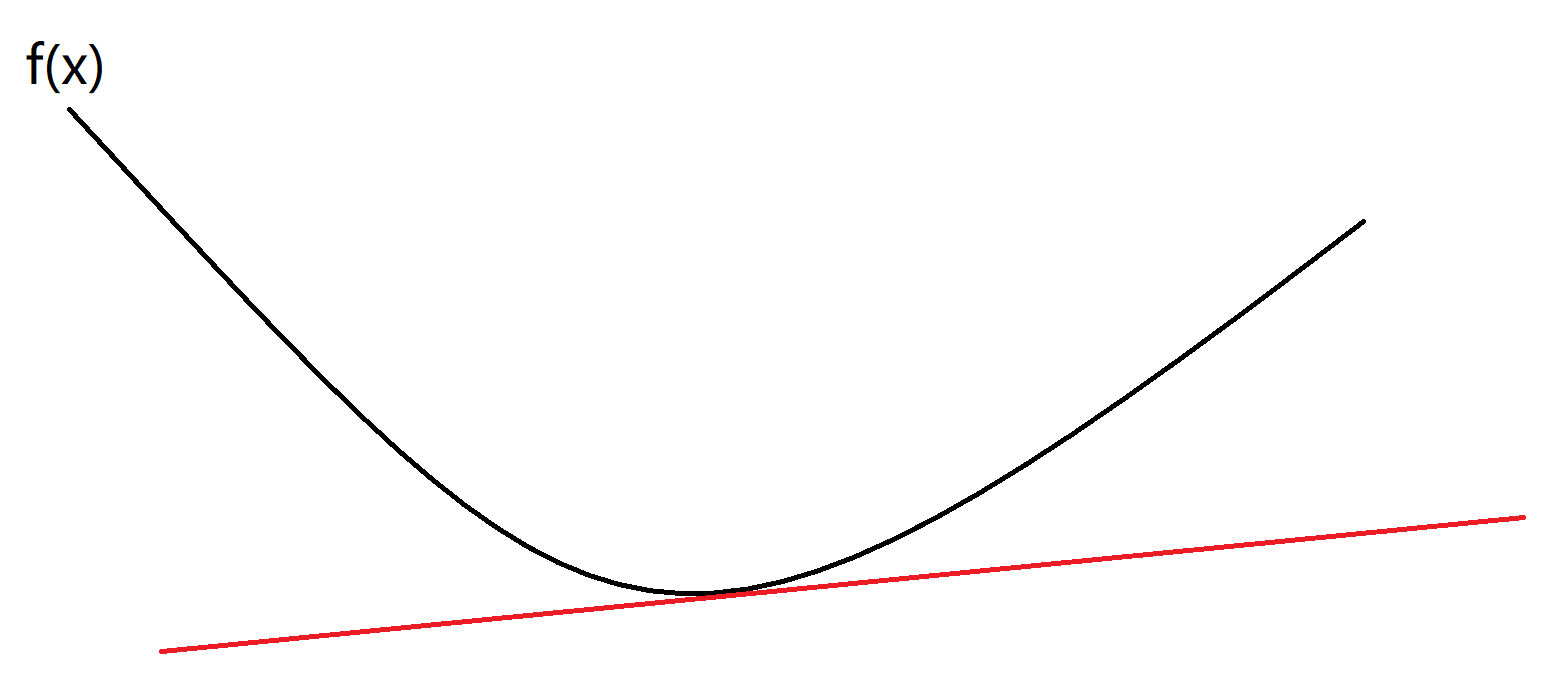
如下图所示\(z=f(x,y)\),\(g(x,y)=0\),如果我们需要求\(z\)在\(g(x,y)\)条件下的极值。从几何角度来说,我们可以画出\(z = C_i\)的等高线,等高线与\(g(x,y)\)相切的点\((x_0,y_0)\)即为极值点。如下图所示:

因为在点\((x_0,y_0)\)取得极值,那么,\(\nabla{f(x_0, y_0)} // \nabla{g(x_0, y_0)}\),也就是说此时梯度平行。也就是说\(({f_x}'(x_0,y_0),{f_y}'(x_0,y_0)) // ({g_x}'(x_0,y_0),{g_y}'(x_0,y_0))\)(这个是可以证明的,但是在这里就不证明了)因此有:
\[\frac{{f_x}'(x_0,y_0)}{{g_x}'(x_0,y_0)}=\frac{{f_y}'(x_0,y_0)}{{g_y}'(x_0,y_0)}=-\lambda_0 (\lambda_0可以为0)
\]
即:
\[\left\{\begin{matrix}
{f_x}'(x_0,y_0)+\lambda_0{g_x}'(x_0,y_0)=0\\
\\
{f_y}'(x_0,y_0)+\lambda_0{g_y}'(x_0,y_0)=0\\
\\
g(x,y)=0
\end{matrix}\right. \tag{6}
\]
如果此时我们有一个辅助函数\(L(x,y, \lambda)=f(x,y)+\lambda g(x,y)\),对其求偏导然后求极值点可得:
\[\left\{\begin{matrix}
\frac{\partial L(x,y, \lambda)}{\partial x}={f_x}'(x,y)+\lambda{g_x}'(x,y)=0\\
\\
\frac{\partial L(x,y, \lambda)}{\partial y}={f_y}'(x,y)+\lambda{g_y}'(x,y)=0\\
\\
\frac{\partial L(x,y, \lambda)}{\partial \lambda}=g(x,y)=0
\end{matrix}\right. \tag{7}
\]
显而易见公式\((6)\)和公式\((7)\)相等。因此我们对\(z = f(x,y)\)在条件\(f(x,y) = 0\)的条件下求极值\((x_0,y_0)\)的问题变成了求拉格朗日函数\(L(x,y, \lambda)=f(x,y)+\lambda g(x,y)\)偏导数为0的解。
KKT条件(Karush-Kuhn-Tucker Conditions)
上面我们讨论的是在等式约束条件下求函数极值的问题(也就是\(g(x,y)=0\))but,如果如果是不等式条件下,我们应该如何来使用拉格朗日函数来求解呢?下面引出KKT条件。
什么是KKT条件呢?它是在满足一些有规则的条件下,一个非线性规划问题能有最优化解法的一个必要条件。也就是说优化问题在最优值处必须满足KKT条件。
例如我们有以下优化问题:
\[\begin{equation}\begin{aligned}
\min _{x} & f(x) \\
\text { s.t. } & h_{i}(x)=0 \quad(i=1, \ldots, m) \\
& g_{j}(x) \leqslant 0 \quad(j=1, \ldots, n)
\end{aligned}\end{equation}
\]
其拉格朗日函数为:
\[\begin{equation}L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x})\end{equation} \tag{8}
\]
则其KKT条件为:
\[\begin{equation}\left\{\begin{array}{l}
g_{j}(\boldsymbol{x}) \leqslant 0 \\
\mu_{j} \geqslant 0 \\
\mu_{j} g_{j}(\boldsymbol{x})=0 \\
h(x) =0
\end{array}\right.\end{equation}
\]
接下来让我们来解释一下为什么是这样的。(不一定是数学证明)。
下面我们只讨论\(f(x)\)在不等式\(g_i(x)<0\)条件下取\(min\)情况。这里可能有人会说,如果我要求\(max\)怎么办?很简单那,将\(f(x)\)取反即可,就变成了求\(min\)的情况。同样对于\(g_i(x) > 0\)的情况,我们取反就变成了\(g^{'}(x) = -g_i(x) \lt 0\)。
对于上述讨论,有两种情况如下图(图中\(x^*\)代表极小值点):
- 情况一:极小值点\(x^*\)在\(g_i(x)<0\)的区域内
- 情况二:极小值点\(x^*\)在\(g_i(x)=0\)上
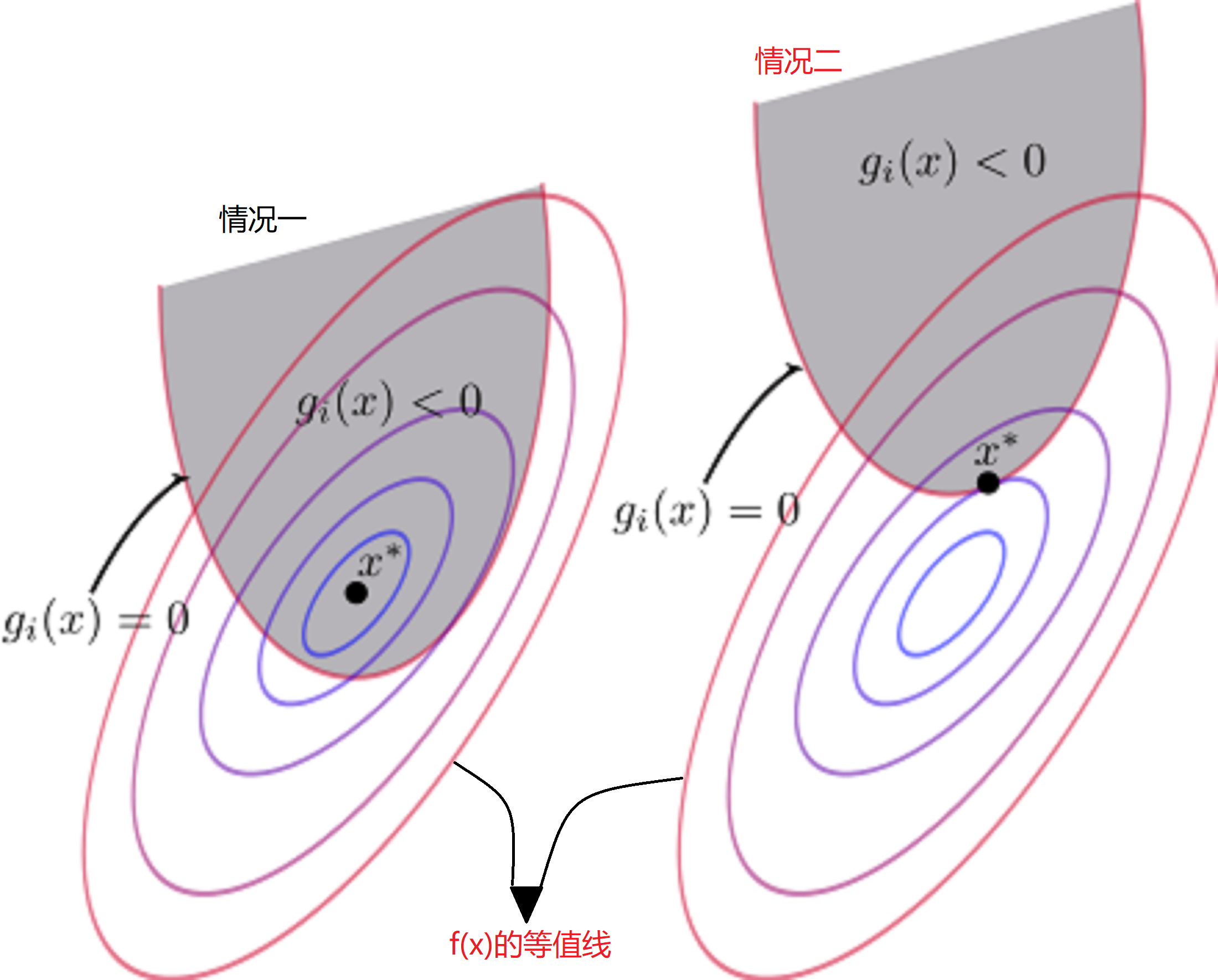
首先我们先讨论情况二,对于情况二很好理解,此时的“不等式约束”变成了“等式约束”。那么其在极值点满足以下条件:
\[h(x)=0\\
g(x)=0\\
\mu \geq 0 \tag{9}
\]
\(h(x)=0,g(x)=0\)我们很好理解,但是为什么我们对\(\mu\)还要进行限制呢?然后为什么限制还为\(\mu \geq 0\)呢?首先我们来考虑一下\(f(x)\)和\(g(x)\)在\(x^*\)点的梯度方向(首先\(f(x)\)和\(g(x)\)在\(x^*\)点的梯度方向肯定是平行的【梯度的方向代表函数值增加最快的方向】)。
- 对于\(f(x)\)来说,等值线大小由中心到周围逐渐增大,因此它的梯度方向指向可行域。为图中红色的箭头号。
- 对于\(g(x)\)来说,梯度方向肯定是指向大于0的一侧,那么就是要背离可行域。为图中黄色的箭头号。
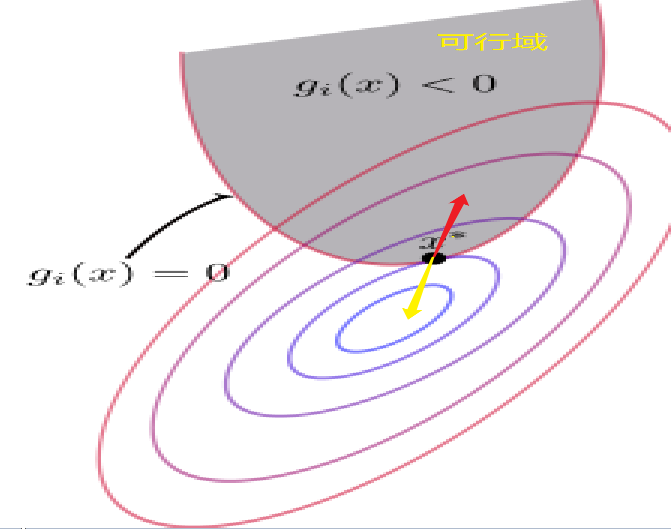
在前面拉格朗日乘子法中我们有以下推导:
\[\frac{{f_x}'(x_0,y_0)}{{g_x}'(x_0,y_0)}=\frac{{f_y}'(x_0,y_0)}{{g_y}'(x_0,y_0)}=-\lambda_0 (\lambda_0可以为0)
\]
又因为\(g(x)\)和\(f(x)\)梯度方向相反,因此\(\lambda_0 \geq0\)。 因此对于\(公式9\)有\(\mu \geq 0\)。
接下来让我们来讨论情况一。情况一是极小值$x^* \(在\)g(x)$的可行域中,因此,我们可以将其看成没有不等式约束条件。那么其在极值点满足以下条件:
\[h(x)=0\\
g(x) \leq 0\\
\mu =0
\]
对比两种情况:
- 情况一:\(\mu = 0,g(x) \leq 0\)
- 情况二:\(\mu \geq 0,g(x)=0\)
综合情况一和情况二,可得到KKT条件为:
\[\begin{equation}\left\{\begin{array}{l}
g_{j}(\boldsymbol{x}) \leqslant 0 \quad(主问题可行)\\
\mu_{j} \geqslant 0 \quad(对偶问题可行)\\
\mu_{j} g_{j}(\boldsymbol{x})=0 \quad(互补松弛)\\
h(x) =0
\end{array}\right.\end{equation}
\]
拉格朗日乘子法对偶问题
对于如下优化问题:
\[\begin{equation}\begin{aligned}
\min _{x} & f(x) \\
\text { s.t. } & h_{i}(x)=0 \quad(i=1, \ldots, m) \\
& g_{j}(x) \leqslant 0 \quad(j=1, \ldots, n)
\end{aligned}\end{equation} \tag{10}
\]
其拉格朗日函数为:
\[\begin{equation}
L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x}) \\
s.t. \mu_j \ge0
\end{equation}
\]
对于上述的优化问题(\(公式10\))我们可以等价于(下面的称之为主问题):
\[\begin{equation}\begin{aligned}
\min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} & \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\
\text { s.t. } & \mu_{i} \geq 0, \quad i=1,2, \ldots, m
\end{aligned}\end{equation}
\]
证明如下:
\[\begin{equation}\begin{aligned}
& \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}}\mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\
=& \min _{\boldsymbol{x}}\left(f(\boldsymbol{x})+\max _{\boldsymbol{\lambda}, \boldsymbol{\mu}}\left(\sum_{i=1}^{m} \mu_{i} g_{i}(\boldsymbol{u})+\sum_{j=1}^{n} \lambda_{j} h_{j}(\boldsymbol{u})\right)\right) \\
=& \min _{\boldsymbol{x}}\left(f(\boldsymbol{x})+\left\{\begin{array}{l}
0 \text{ 若x满足约束}\\
\infty \text{否则}
\end{array}\right)\right.\\
=& \min _{\boldsymbol{u}} f(\boldsymbol{u})
\end{aligned}\end{equation}
\]
其中, 当\(g_i(x)\)不满足约束时, 即\(g_i(x)\gt0\), 我们可以令\(\mu=\infty\), 使得\(\mu_ig_i(x) = \infty\); 当\(h_j(x)\)不满足约束时, 即 \(h_j(x)\ne0\), 我们可以取\(\lambda_j = \infty\), 使得\(\lambda_jh_j(x) = \infty\)。当\(x\)满足约束时, 由于 \(\mu_i\ge0\),\(g_i(x)\le0\), 则 \(\mu_ig_j(x)\le0\),因此我们可以取最大值0。 实际上也就是说如果\(公式10\)存在最优解,则最优解必须满足KKT条件。
对于\(公式10\)其对偶问题为:
\[\begin{equation}\begin{aligned}
\max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \min _{x}& \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\
\text { s.t. } & \mu_{i} \geq 0, \quad i=1,2, \ldots, m
\end{aligned}\end{equation}
\]
对偶问题是主问题的下界(他们两个具有弱对偶性):
\[p^* = \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \ge \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \min _{x} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = g^*
\]
你可以记忆成“廋死的骆驼比马大”,还看到一个记忆方法为“宁为凤尾不为鸡头”。hhh
证明如下:
\[\max _{x} \min _{y} f(x, y) \leq \min _{y} \max _{x} f(x, y)\\
\text{let } g(x)=\min _{y} f(x, y)\\
\text{then }g(x) \leq f(x, y), \forall y\\
\therefore \max _{x} g(x) \leq \max _{x} f(x, y), \forall y\\
\therefore \max _{x} g(x) \leq \min _{y} \max _{x} f(x, y)
\]
Slater 条件
前面我们讨论了弱对偶性,这里我们将进行讨论Slater条件,但是为什么我们要讨论Slater条件呢?原因很简单,我们想让上面的弱对偶问题转成强对偶问题。
Slater定理是说,当Slater条件成立且原问题是凸优化问题时,则强对偶性成立。这里有几个名词值得注意:
-
凸优化问题
如果一个优化问题满足如下格式,我们就称该问题为一个凸优化问题:
\[\begin{array}{}
\text{min}&f(x)\\
\text{s.t}&g_i(x)\le0,&i=1,...,m \\
\text{ }&h_i(x)=0,&i=1,...,p
\end{array}
\]
其中\(f(x)\)是凸函数,不等式约束\(g(x)\)也是凸函数,等式约束\(h(x)\)是仿射函数。
-
凸函数是具有如下特性的一个定义在某个向量空间的凸子集\(C\)(区间)上的实值函数\(f\):对其定义域上任意两点\(x_1,x_2\)总有\(f\left(\frac{x_{1}+x_{2}}{2}\right) \leq \frac{f\left(x_{1}\right)+f\left(x_{2}\right)}{2}\)。
-
仿射函数
仿射函数,即最高次数为1的多项式函数。
-
强对偶性
弱对偶性是\(p* = \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \ge \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \min _{x} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = g*\),也就是\(p^* \ge g^*\),则强对偶性是\(p^* = g^*\)。
说了这么多,那什么是Slater条件呢?
- 原问题是凸优化问题
- 存在\(x\)使得\(g(x) \le0\)严格成立。(换句话说,就是存在\(x\)使得\(g(x) \lt0\)成立)
值得注意的是线性支持向量机满足Slater条件(因为\(\frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}\)和\(1-y_{i}(w^Tx_i+b)\)均为凸函数),也就是它满足强对偶性。
最大间隔分类器与拉格朗日乘子法
前面说了这么多,实际上也就是为这个地方做铺垫。我们可以将最大间隔分类问题转化成在KKT条件下的拉格朗日函数的极值问题,然后又因为其满足Slater条件,我们可以转化成强对偶问题。
在最大间隔分类中,我们得到如下结论:
\[\left \{ \begin{matrix} \begin{align*}
& \min \quad \frac{1}{2}\| \omega \|^2 \\
& s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m
\end{align*} \end{matrix} \right. \tag{11}
\]
其拉格朗日函数为:
\[\begin{equation}
\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha}):=\frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b\right)\right) \\
s.t. \alpha_i \ge0,\quad i=1,2,...,m
\end{equation}
\]
其对偶问题(满足强对偶性)为:
\[\begin{equation}\begin{aligned}
&\max _{\alpha} \min _{\boldsymbol{w}, b}\left(\frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b\right)\right)\right)\\
&\text { s.t. } \quad \alpha_{i} \geq 0, \quad i=1,2, \ldots, m
\end{aligned}\end{equation}\tag{12}
\]
然后我们来求:
\[\begin{equation}\begin{aligned}
&\min _{\boldsymbol{w}, b}\left( \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b\right)\right)\right)\\
&\text { s.t. } \quad \alpha_{i} \geq 0, \quad i=1,2, \ldots, m
\end{aligned}\end{equation}
\]
上式对于\((\omega,b)\)属于无约束优化问题,令偏导为零可得:
\[\begin{equation}
\frac{\partial \mathcal{L}}{\partial \boldsymbol{w}}=\mathbf{0} \Rightarrow \boldsymbol{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i} \\
\frac{\partial \mathcal{L}}{\partial b}=0 \Rightarrow \sum_{i=1}^{m} \alpha_{i} y_{i}=0
\end{equation} \tag{13}
\]
代入\(公式(12)\)消去\((\omega,b)\)可得:
\[\begin{equation}\begin{aligned}
\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\top} \boldsymbol{x}_{j}-\sum_{i=1}^{m} \alpha_{i} \\
\text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\
& \alpha_{i} \geq 0, \quad i=1,2, \ldots, m
\end{aligned}\end{equation} \tag{14}
\]
因此问题变成了寻找合适的\(\alpha\)使得\(公式(12)\)成立。
又因为\(公式(11)\)在极值点必定满足KKT条件。也就是说\(\alpha_i(1-y_{i}({w}^{\top} {x}_{i}+b))=0\),当\(\alpha_i \gt 0\)时必有\(1-y_{i}({w}^{\top} {x}_{i}+b) =0\)。因此对于\(\alpha_i \gt0\)对应的样本是支持向量,对于非支持向量,则\(\alpha_i =0\)
对于\(公式13\)有:
\[\begin{equation}\begin{aligned}
\boldsymbol{w} &=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i} \\
&=\sum_{i: \alpha_{i}=0}^{m} 0 \cdot y_{i} \boldsymbol{x}_{i}+\sum_{i: \alpha_{i}>0}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i} \\
&=\sum_{i \in S V} \alpha_{i} y_{i} \boldsymbol{x}_{i}\quad(SV 代表所有支持向量的集合)
\end{aligned}\end{equation}
\]
然后我们可以求\(b\)了,对于支持向量有\(y_k =\omega^{\top}x+b\),因此:
\[\begin{equation}\begin{aligned}
b&=y_k-\boldsymbol{w}^{\top} \boldsymbol{x} \\
&=y_{k}-(\sum_{i \in S V} \alpha_{i} y_{i} \boldsymbol{x}_{i})^{\top}x_k \\
&=y_k-\sum_{i \in S V} \alpha_{i} y_{i} \boldsymbol{x}_{i}^{\top}x_k
\end{aligned}
\end{equation}
\]
通过上面的推导,我们能够知道支持向量机的\((\omega,b)\)仅由支持向量决定。实践中, 为了得到对 $b \(更稳健的估计, 通常使用对所有支持向量求解得到\)b$的平均值。
综上,我们想计算出合适的\(\omega\)和\(b\),就必须计算出\(\alpha_i\),然后我们就可以得到支持向量,在然后我们我们通过支持向量和\(\alpha_i\)就可以计算出\(\omega\)和\(b\)。
至于怎么求\(\alpha_i\),我们使用可以使用后面介绍的SMO算法求解,首先我们来介绍一下核方法。
核技巧
在前面的讨论中,我们对样本的考虑都是线性可分的。但是实际上,大部分的情况下,数据都是非线性可分的。比如说异或问题。在前面的章节神经网络中,我们是通过使用增加一层隐层来解决这个问题,那么对于SVM我们应该怎么解决呢?SVM中使用核技巧(kernel trick)来解决非线性问题。

既然在原始的特征空间\(\mathbb{R}^{d}\)不是线性可分的,支持向量机希望通过一个映射\(\phi: \mathbb{R}^{d} \rightarrow \mathbb{R}^{\tilde{d}}\), 使得数据在新的空间\(\mathbb{R}^{\tilde{d}}\)是线性可分的。可以证明(但是我证明不出),当\(d\)有限时, 一定存在\(\tilde{d}\), 使得样本在空间$ \mathbb{R}^{\tilde{d}}$中线性可分。
核函数
令\(\phi(x)\)为\(x\)映射后的特征向量,因此划分的超平面可以表示为\(f(x)=\phi(x)+b\)。同时\(公式(11)\)可以改为:
\[\begin{equation}\begin{array}{l}
\min _{w,b} \frac{1}{2}\|\boldsymbol{w}\|^{2} \\
\text { s.t. } y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \phi\left(\boldsymbol{x}_{i}\right)+b\right) \geqslant 1, \quad i=1,2, \ldots, m
\end{array}\end{equation}
\]
然后\(公式14\)可以写成如下的形式:
\[\begin{equation}\begin{aligned}
\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \phi(\boldsymbol{x}_{i}^{\top}) \phi(\boldsymbol{x}_{j})-\sum_{i=1}^{m} \alpha_{i} \\
\text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\
& \alpha_{i} \geq 0, \quad i=1,2, \ldots, m
\end{aligned}\end{equation} \tag{15}
\]
求解\(公式15\)面临一个很大的问题,那就是\(\phi(\boldsymbol{x}_{i}^{\top})\)和\(\phi(\boldsymbol{x}_{j})\)很难计算(一般来说它们都是高维的甚至无穷维),首先需要计算特征在\(\mathbb{R}^{\tilde{d}}\)的映射,然后又要计算在他的内积,复杂度为$$\mathcal{O}(\tilde{d})$$。因此我们通过使用核技巧,将这两步并将复杂度降低到\(\mathbb{R}^{d}\)。即核技巧希望构造一个核函数\(\kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)\),使得:
\[\begin{equation}\kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{j}\right)\end{equation}
\]
实际上核函数不仅仅只用于SVM,对于所有涉及到向量内积的运算,我们都可以使用核函数来解决。
因此\(公式15\)可以改写成:
\[\begin{equation}\begin{aligned}
\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)-\sum_{i=1}^{m} \alpha_{i} \\
\text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\
& \alpha_{i} \geq 0, \quad i=1,2, \ldots, m
\end{aligned}\end{equation} \tag{15}
\]
对于核函数来说,我们可以自己造,但是通常我们会从一些常见的核函数中进行选择:根据不同问题选择不同的参数。下图是是一些常见的核函数。

软间隔
前面我们讨论的情况都是超平面都是能够完美的将数据进行分开(即使是非线性数据,我们使用核函数进行骚操作然后进行分割),这种所有样本都满足约束的情况称之为硬间隔(hard margin),但实际上数据是有噪音的,如果使用核函数进行骚操作,然后在找到一个线性可分超平面,可能就会造成模型过拟合,同样也可能我们找不到合适的核函数。因此,我们将标准放宽,允许一定的“错误”,称之为软间隔(soft margin):
我们希望在优化间隔的同时,允许错误样本的出现,但是我们同样希望出现错误的样本越少越好。因此优化目标\(公式(5)\)可写成:
\[\left \{ \begin{matrix} \begin{align*}
& min _{\boldsymbol{w}, b} \left(\frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \ell_{0 / 1}\left(y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)-1\right)\right)\\
& s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m
\end{align*} \end{matrix} \right.
\tag{16}
\]
其中\(C \gt 0\)是一个常数,\(\ell_{0 / 1}\)是“0/1损失函数”。
\[\begin{equation}\ell_{0 / 1}(z)=\left\{\begin{array}{ll}
1, & \text { if } z<0 \\
0, & \text { otherwise }
\end{array}\right.\end{equation}
\]
可以很简单的知道,\(C\)取无穷大时,\(公式(16)\)迫使所有样本均满足约束。当\(C\)取有限值时,允许一些样本不满足约束。but,还是有些问题,\(\ell_{0 / 1}\)是非凸,非连续的一个函数,会使得上式\((16)\)变得不好求解,因此人们通常使用其他的函数来替代\(\ell_{0 / 1}\),称之为“替代损失(surrogate loss)”。下面是几种常用的替代损失函数:
\[\begin{equation}\begin{aligned}
&\text {hinge 损失}:\ell_{\text {hinge}}(z)=\max (0,1-z) \\
&\text { 指数损失(exponential loss): } \ell_{\exp }(z)=\exp (-z)\\
&\text { 对率损失(logistic loss): } \ell_{\log }(z)=\log (1+\exp (-z))
\end{aligned}\end{equation}
\]
对应的图如下:
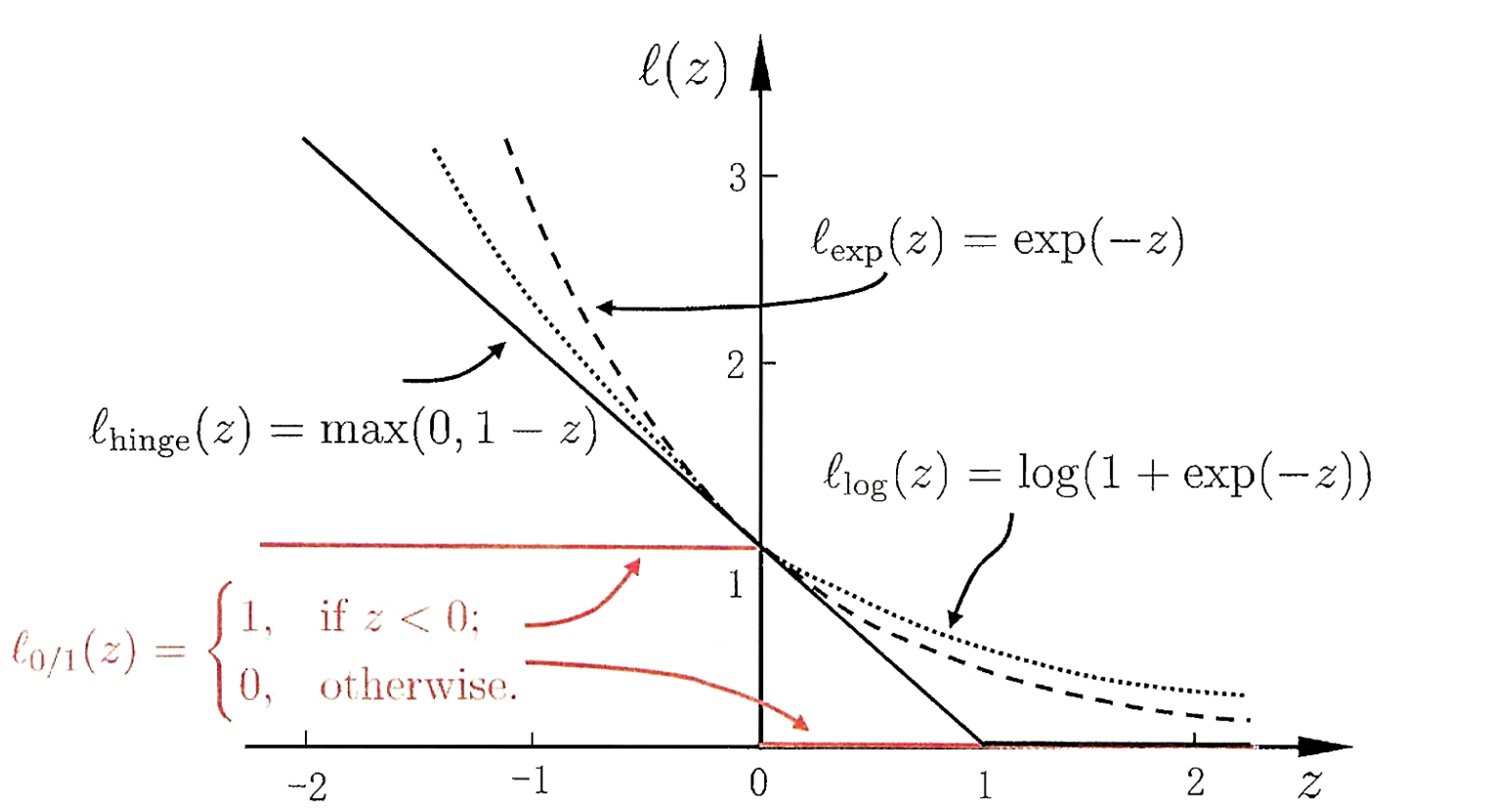
下面将以\(hinge函数\)为例子介绍软间隔支持向量机的推导。
软间隔支持向量机推导
\(\text {hinge函数}:\ell_{\text {hinge}}(z)=\max (0,1-z)\)等价于:
\[\begin{equation}\xi_{i}=\left\{\begin{array}{ll}0 & \text { if } y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right) \geq 1 \\1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right) & \text { otherwise }\end{array}\right.\end{equation}
\]
\(\xi_{i}\)我们称之为松弛变量(slack variable),样本违背约束越远,则松弛变量值越大。因此优化目标式\((5)\)可以写成:
\[\begin{equation}\begin{aligned}\min _{\boldsymbol{w}, b, \boldsymbol{\xi}} &( \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+C \sum_{i=1}^{m} \xi_{i} )\\\text { s.t. } & y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right) \geq 1-\xi_{i}, \quad i=1,2, \ldots, m \\& \xi_{i} \geq 0, \quad i=1,2, \ldots, m\end{aligned}\end{equation} \tag{17}
\]
同样在这里\(C\)越大,代表我们希望越多的样本满足约束。软间隔的拉格朗日函数为:
\[\begin{equation}\begin{aligned}
\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\beta}):=& \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+C \sum_{i=1}^{m} \xi_{i} \\
&+\sum_{i=1}^{m} \alpha_{i}\left(1-\xi_{i}-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right)\right) \\
&+\sum_{i=1}^{m} \beta_{i}\left(-\xi_{i}\right)
\end{aligned}\end{equation} \tag{18}
\]
其KKT条件为:
\[\begin{equation}\left\{\begin{array}{l}
1 - \xi_{i}-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right) \leq 0,-\xi_{i} \leq 0 \quad(主问题可行)\\
\alpha_{i} \geq 0, \beta_{i} \geq 0 \quad(对偶问题可行)\\
\alpha_{i}\left(1-\xi_{i}-y_{i}\left(\boldsymbol{w}^{\top} \phi\left(\boldsymbol{x}_{i}\right)+b\right)\right)=0, \beta_{i} \xi_{i}=0 \quad(互补松弛)\\
\end{array}\right.\end{equation}
\]
其对偶问题为:
\[\begin{equation}\begin{aligned}
\max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \min _{\boldsymbol{w}, b, \boldsymbol{\xi}} & \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \\
\text { s.t. } & \alpha_{i} \geq 0, \quad i=1,2, \ldots, m \\
& \beta_{i} \geq 0, \quad i=1,2, \ldots, m
\end{aligned}\end{equation}
\]
\(\min _{\boldsymbol{w}, b, \boldsymbol{\xi}} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\beta})\)的优化属于无约束的优化问题,我们通过将偏导置零的方法得到\((\boldsymbol{w}, b, \boldsymbol{\xi})\)的最优值:
\[\begin{equation}\begin{aligned}
\frac{\partial \mathcal{L}}{\partial \boldsymbol{w}}=\mathbf{0} & \Rightarrow \boldsymbol{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right) \\
\frac{\partial \mathcal{L}}{\partial b} &=0 \Rightarrow \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\
\frac{\partial \mathcal{L}}{\partial \boldsymbol{\xi}} &=\mathbf{0} \Rightarrow \alpha_{i}+\beta_{i}=C
\end{aligned}\end{equation}\tag{19}
\]
因为\(\beta_{i}=C -\alpha_{i} \ge0\),因此我们约束\(0 \le \alpha_i \le C\),将\(\beta_{i}=C -\alpha_{i},{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)\),代入式\((18)\)可得:
\[\begin{equation}\begin{array}{ll}
\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \phi\left(\boldsymbol{x}_{i}\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{j}\right)-\sum_{i=1}^{m} \alpha_{i} \\
\text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0,\\
& 0 \le \alpha_i \le C
\end{array}\end{equation} \tag{20}
\]
如果我们将式\((17)\)看成如下一般形式:
\[\begin{equation}\min _{f} (\Omega(f)+C \sum_{i=1}^{m} \ell\left(f\left(\boldsymbol{x}_{i}\right), y_{i}\right))\end{equation}
\]
对于\(\Omega(f)\)我们称之为“结构风险(structural risk)”,第二项\(\sum_{i=1}^{m} \ell\left(f\left(\boldsymbol{x}_{i}\right), y_{i}\right)\)称之为“经验分享(empirical risk)“,而\(C\)的作用就是对两者进行折中。
SMO算法
前面说了这么多,终于终于,我们要开始说SMO(Sequential minimal optimization,序列最小化)算法了。首先说一下这个算法的目的,这个算法就是用来求\(\alpha_i\)的。SMO算法是一种启发式算法,基本思路是如果所有变量的解都满足最优化问题的KKT条件,则该最优化问题的解就得到了。
对于式\((19)\)如果我们将\(\phi({x}_{i})^{\top} {\phi}(\boldsymbol{x}_{j})\)使用核函数来表示则有:
\[\begin{equation}\begin{aligned}
\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\
\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\
& 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N
\end{aligned}\end{equation} \tag{21}
\]
假如我们选择\(\alpha_1,\alpha_2\)作为变量(至于为什么不是只选择一个变量是因为存在\(\sum_{i=1}^{N} \alpha_{i} y_{i}=0\)这个约束条件),固定其他变量\(\alpha_{i}(i=3,4, \cdots, N)\),则式\((20)\)问题可以变成:
\[\begin{equation}\begin{array}{rl}
\min _{\alpha_{1}, \alpha_{2}} & W\left(\alpha_{1}, \alpha_{2}\right)=\frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2}- \\
& \left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 2} \\
\text { s.t. } & \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\varsigma \\
& 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2
\end{array}\end{equation} \tag{22}
\]
在式\((21)\)中省略了\(\sum_{i=3}^N\alpha_i\)这个式子,是因为该式为常数项。
因为\(\alpha_{1} y_{1}+\alpha_{2} y_{2} = 常数,y_1 = \pm1,y_2=\pm1\),因此有:
\[\begin{equation}\left\{\begin{array}{l}
\alpha_1 - \alpha_2 = k \quad(y_1 \ne y_2)\\
\alpha_1 + \alpha_2 = k \quad(y_1 = y_2)\\
\end{array}
\right.
\end{equation}
\quad \text { s.t. }0 \leqslant \alpha_{1} \leqslant C,0 \leqslant \alpha_{2} \leqslant C\\ \tag{23}
\]
我们可以将式\((22)\)用图表示出来:

因为\(\alpha_1\)和\(\alpha_2\)存在线性关系,这样两个变量的最优化问题成为了实质上单变量的最优化问题,因此,我们可以看成其为变量\(\alpha_2\)的最优化问题。
设\(式(22)\)的初始可行解为\(\alpha_{1}^{\text {old }}, \alpha_{2}^{\text {old }}\),最优解为\(\alpha_{1}^{\text {new }}, \alpha_{2}^{\text {new}}\)。对于\(\alpha_i^{new}\)来说,其取值范围必须满足:
\[L \leqslant \alpha_{i}^{\text {new }} \leqslant H
\]
- 情况1:\(L=\max \left(0, \alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right), \quad H=\min \left(C, C+\alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right)\)
- 情况2:\(L=\max \left(0, \alpha_{2}^{\text {old }}+\alpha_{1}^{\text {old }}-C\right), \quad H=\min \left(C, \alpha_{2}^{\text {old }}+\alpha_{1}^{\text {old }}\right)\)
设我们计算出来的\(\alpha_2\)为\(\alpha_2^{new,unc}\),则有:
\[\alpha_2^{new}= \begin{cases} H& { \alpha_2^{new,unc} > H}\\ \alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc} \leq H}\\ L& {\alpha_2^{new,unc} < L} \end{cases}
\]
那么问题就回到了如果我们有\(\alpha_2^{old}\)我们如何得到\(\alpha_2^{new,unc}\)呢?
首先我们设一个超平面函数\(g(x)\)如下:
\[设:g(x) = w^{*} \bullet \phi(x) + b\\
由式(19)可知{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} {\phi}({x}_{i}) \\
因此有:
g(x)=\sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x, x_j)+ b^{*}
\]
然后我们令
\[\begin{equation}E_{i}=g\left(x_{i}\right)-y_{i}=\left(\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{j}, x_{i}\right)+b\right)-y_{i}, \quad i=1,2\end{equation}
\]
同时引进记号:
\[\begin{equation}v_{i}=\sum_{j=3}^{N} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)=g\left(x_{i}\right)-\sum_{j=1}^{2} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)-b, \quad i=1,2\end{equation}
\]
因此式\((22)\)可以改写成:
\[\begin{equation}\begin{array}{c}
W\left(\alpha_{1}, \alpha_{2}\right)=| \frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2}- \\
\left(\alpha_{1}+\alpha_{2}\right)+y_{1} v_{1} \alpha_{1}+y_{2} v_{2} \alpha_{2}
\end{array}\end{equation} \tag{24}
\]
又因为\(\alpha_{1} y_{1}+\alpha_{2} y_{2}=\varsigma,\quad y_iy_i = 1\),因此\(\alpha_1\)可以表示为:
\[\begin{equation}\alpha_{1}=\left(\varsigma-y_{2} \alpha_{2}\right) y_{1}\end{equation}
\]
代入式\((24)\)中,我们有:
\[\begin{equation}\begin{aligned}
W\left(\alpha_{2}\right)=& \frac{1}{2} K_{11}\left(s-\alpha_{2} y_{2}\right)^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{2} K_{12}\left(s-\alpha_{2} y_{2}\right) \alpha_{2}-\\
&\left(s-\alpha_{2} y_{2}\right) y_{1}-\alpha_{2}+v_{1}\left(s-\alpha_{2} y_{2}\right)+y_{2} v_{2} \alpha_{2}
\end{aligned}\end{equation}
\]
然后,我们对\(\alpha_2\)求导数:
\[\begin{equation}\begin{aligned}
\frac{\partial W}{\partial \alpha_{2}}=& K_{11} \alpha_{2}+K_{22} \alpha_{2}-2 K_{12} \alpha_{2}-\\
& K_{11 S} y_{2}+K_{12} s y_{2}+y_{1} y_{2}-1-v_{1} y_{2}+y_{2} v_{2}
\end{aligned}\end{equation}
\]
令其导数为0可得:
\[\begin{equation}\begin{aligned}
\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}=& y_{2}\left(y_{2}-y_{1}+\varsigma K_{11}-\varsigma K_{12}+v_{1}-v_{2}\right) \\
=& y_{2}\left[y_{2}-y_{1}+\varsigma K_{11}-\varsigma K_{12}+\left(g\left(x_{1}\right)-\sum_{j=1}^{2} y_{j} \alpha_{j} K_{1 j}-b\right)-\right.\\
&\left.\left(g\left(x_{2}\right)-\sum_{j=1}^{2} y_{j} \alpha_{j} K_{2 j}-b\right)\right]
\end{aligned}\end{equation} \tag{25}
\]
又因为\(\varsigma=\alpha_{1}^{\mathrm{old}} y_{1}+\alpha_{2}^{\mathrm{old}} y_{2}\)代入式\((25)\)可得:
\[\begin{equation}\begin{aligned}
\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {new }, \text { unc }} &=y_{2}\left(\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {old }} y_{2}+y_{2}-y_{1}+g\left(x_{1}\right)-g\left(x_{2}\right)\right) \\
&=\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {old }}+y_{2}\left(E_{1}-E_{2}\right)
\end{aligned}\end{equation} \tag{26}
\]
令:
\[\begin{equation}\eta=K_{11}+K_{22}-2 K_{12}=\left\|\Phi\left(x_{1}\right)-\Phi\left(x_{2}\right)\right\|^{2}\end{equation}
\]
因此式\((26)\)可化简为:
\[\begin{equation}\alpha_{2}^{\text {new }, \mathrm{unc}}=\alpha_{2}^{\text {old }}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{\eta}\end{equation} \tag{27}
\]
同时有:
\[\alpha_2^{new}= \begin{cases} H& { \alpha_2^{new,unc} > H}\\ \alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc} \leq H}\\ L& {\alpha_2^{new,unc} < L} \end{cases}
\]
因为我们已经得到\(\alpha_2^{new}\),根据\(\alpha_1^{new}\)和\(\alpha_2^{new}\)之间的线性关系,我们可以就可以得到\(\alpha_1^{new}\)了。
我们每次完成两个变量的优化之后,都需要重新更新阈值。具体更新可以看下面部分。
SMO变量的选择方法
通过前面部分我们知道SMO算法就是选择两个变量进行优化,其中至少有一个变量是违反了KKT条件(假如没有违反的话,我们也就没必要进行计算了)。我们可以使用\(\alpha_1\)代表第一个变量,\(\alpha_2\)代表第二个变量。
-
第一个变量的选择
我们称第一个变量的选择为外层循环,外层循环在训练样本中选择违反KKT条件最严重的样本点。对于KKT条件,我们可以转成以下的形式:
\[\begin{equation}\begin{aligned}
\alpha_{i} &=0 \Leftrightarrow y_{i} g\left(x_{i}\right) \geqslant 1 &\quad(1)\\
0<\alpha_{i} &<C \Leftrightarrow y_{i} g\left(x_{i}\right)=1 &\quad(2)\\
\alpha_{i} &=C \Leftrightarrow y_{i} g\left(x_{i}\right) \leqslant 1 &\quad(3)\\
其中g(x_{i}) &= \sum_{j=1}^{N}\alpha_{j}y_{j}K(x_{i},x_{j})+b\\
\end{aligned}\end{equation} \tag{28}
\]
证明如下:
对于上式\((1)\):
\[\begin{equation}\begin{aligned}
&\because\alpha_i = 0,\alpha_i + \beta_i = C ,且在KKT条件\beta_{i}\xi_{i}=0\\
&\therefore \beta_i = C,\therefore\xi_i = 0\\
又&\because 由KTT条件可知:1-\xi_i\le y_ig(x_i),\alpha_{i} [y_{i}g(x_{i})-(1-\xi_{i})]=0\\
&\therefore y_ig(x_i) \ge 1
\end{aligned}\end{equation}
\]
对于上式\((2)\):
\[\begin{equation}\begin{aligned}
&\because0<\alpha_{i} <C ,\alpha_i + \beta_i = C ,且在KKT条件\beta_{i}\xi_{i}=0\\
&\therefore 0 \lt\beta_i \lt C,\therefore\xi_i = 0\\
又&\because 由KTT条件可知:1-\xi_i\le y_ig(x_i),\alpha_{i} [y_{i}g(x_{i})-(1-\xi_{i})]=0\\
&\therefore y_ig(x_i) = 1-\xi_i = 1
\end{aligned}\end{equation}
\]
对于上式\((3)\):
\[\begin{equation}\begin{aligned}
&\because\alpha_i = C,\alpha_i + \beta_i = C ,且在KKT条件\beta_{i}\xi_{i}=0\\
&\therefore \beta_i = 0,\xi_i \ge0\\
又&\because 由KTT条件可知:1-\xi_i\le y_ig(x_i),\alpha_{i} [y_{i}g(x_{i})-(1-\xi_{i})]=0\\
&\therefore y_ig(x_i) = 1-\xi_i \le 1
\end{aligned}\end{equation}
\]
当然我们也可以给定一定的精度范围\(\varepsilon\),此时KKT条件就变成了:
\[\begin{equation}\begin{array}{l}
a_{i}=0 \Leftrightarrow y_{i} g\left(x_{i}\right) \geq 1-\varepsilon \\
0<a_{i}<C \Leftrightarrow 1-\varepsilon \leq y_{i} g\left(x_{i}\right) \leq 1+\varepsilon \\
a_{i}=C \Leftrightarrow y_{i} g\left(x_{i}\right) \leq 1+\varepsilon
\end{array}\end{equation}
\]
然后我们通过变形后的KKT条件,获得违背的样本点违背最严重的作为第一个变量就🆗了。那么如何度量这个严重性呢?emm,就看\(g\left(x_{i}\right)\)距离KKT条件有多远就行了。
-
第二个变量的选择
第二个变量选择的过程称之为内层循环,其标准是希望能够使\(\alpha_2\)有足够大的变化。由式\((27)\)我们知道:
\[\begin{equation}\alpha_{2}^{\text {new }, \mathrm{unc}}=\alpha_{2}^{\text {old }}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{\eta}\end{equation}
\]
也就是说\(\alpha_2\)的变化量依赖于\(|E_1 - E_2|\),因此我们可以选择式\(|E_1 - E_2|\)最大的\(\alpha_2\)。因为\(\alpha_1\)已经确定,所以\(E_1\)也就已经确定,因此我们只需要确定\(E_2\)即可。如果\(E_1\)为正,则选取\(\alpha_2\)使\(E_2\)最小,如果\(E_1\)为负,则选取\(\alpha_2\)使\(E_2\)最大。
当我们完成两个变量的优化后(优化后的变量),我们就需要来更新阈值\(b\)
- 若更新后的\(0<\alpha_{1} <C\)由式\((28)\)中的式\((2)\)可知:
\[\begin{equation}\sum_{i=1}^{N} \alpha_{i} y_{i} K_{i 1}+b=y_{1}\end{equation}
\]
于是有:
\[\begin{equation}b_{1}^{\mathrm{new}}=y_{1}-\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}-\alpha_{1}^{\mathrm{new}} y_{1} K_{11}-\alpha_{2}^{\mathrm{new}} y_{2} K_{21}\end{equation}
\]
由\(E_i\)的定义式\(\begin{equation}E_{i}=g\left(x_{i}\right)-y_{i}=\left(\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{j}, x_{i}\right)+b\right)-y_{i}, \quad i=1,2\end{equation}\),有:
\[\begin{equation}E_{1}=\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}+\alpha_{1}^{\mathrm{old}} y_{1} K_{11}+\alpha_{2}^{\mathrm{old}} y_{2} K_{21}+b^{\mathrm{old}}-y_{1}\end{equation}
\]
因此则有:
\[\begin{equation}y_{1}-\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}=-E_{1}+\alpha_{1}^{\text {old }} y_{1} K_{11}+\alpha_{2}^{\text {old }} y_{2} K_{21}+b^{\text {old }}\end{equation}
\]
最终:
\[\begin{equation}b_{1}^{\text {new }}=-E_{1}-y_{1} K_{11}\left(\alpha_{1}^{\text {new }}-\alpha_{1}^{\text {old }}\right)-y_{2} K_{21}\left(\alpha_{2}^{\text {new }}-\alpha_{2}^{\text {old }}\right)+b^{\text {old }}\end{equation}
\]
-
同理若$0<\alpha_{2} \lt C $,则有
\[\begin{equation}b_{2}^{\text {new }}=-E_{2}-y_{1} K_{12}\left(\alpha_{1}^{\text {new }}-\alpha_{1}^{\text {old }}\right)-y_{2} K_{22}\left(\alpha_{2}^{\text {new }}-\alpha_{2}^{\text {old }}\right)+b^{\text {old }}\end{equation}
\]
-
若\(\alpha_1^{new},\alpha_2^{new}\)同时满足\(0<\alpha_{i}^{new} \lt C\),则最终:
\[b^{new} = \frac{b_1^{new}+b_2^{new}}{2}
\]
- 若\(\alpha_1^{new},\alpha_2^{new}\)为\(0\)或者\(C\),那么最终:
\[b^{new} = \frac{b_1^{new}+b_2^{new}}{2}
\]
综上:\[\begin{equation}b=\left\{\begin{array}{ll}
b_{1}^{new}, & 0<\alpha_{1}<C \\
b_{2}^{new}, & 0<\alpha_{2}<C \\
\frac{1}{2}\left(b_{1}^{new}+b_{2}^{new}\right), & \text { others }
\end{array}\right.\end{equation}
\]
更新完\(\alpha_1\)和\(\alpha_2\)后我们需要将\(E_i\)进行更新,以便后续的\(\alpha_i\)和\(b\)的求解。
\[\begin{equation}
E_{1}=\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}+\alpha_{1}^{\mathrm{new}} y_{1} K_{11}+\alpha_{2}^{\mathrm{new}} y_{2}K_{21}+b^{\mathrm{new}}-y_{1}\\
E_{2}=\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 2}+\alpha_{1}^{\mathrm{new}} y_{1} K_{12}+\alpha_{2}^{\mathrm{new}} y_{2}K_{22}+b^{\mathrm{new}}-y_{2}\\
\end{equation}
\]
总结
综上,SVM就介绍了,SVM看起来很简单,就是找到一条合适的线能够比较好的分割数据集。为了数值化“比较好”这个词,我们引出了间隔的概念,然后我们希望这个间隔足够大,并且所有的数据完美的分离在间隔的两边。于是这个问题就变成了在一定条件下的极值问题。然后我们选择使用拉格朗日乘子法去解决这个问题,其中在极值点会满足KKT条件。为了简化求解,我们通过Slater条件将问题转成了对偶问题。面对非线性问题,我们选择使用核技巧去解决,同时为了避免过拟合,我们选择使用软间隔;并最终使用SMO算法取得到合适的解。
说实话,本来只是想稍微的介绍一下SVM以及它的原理,自己其实对SVM也是属于之听过没真正的了解过的情况。听别人说SVM不是很难,但是最后却发现emm,越推感觉数学越奇妙。也许上面的内容看起来并不难,但是它却是由前人耗费无数的日日夜夜最终才得出了答案,也许这就是科学的魅力吧!
下面是参考的内容,其中强烈推荐《统计学习方法第2版》
参考

















 浙公网安备 33010602011771号
浙公网安备 33010602011771号