java源码集合体系解析
一、集合体系
1.1 Collection体系
1.1.1 ArrayList & Vector
1)底层实现和特点
底层实现:动态数组实现
特点:元素有序且可重复。Vector是线程安全,ArrayList是线程不安全的。
关系:Vector是JDK1.0就有个类,但是现在所学习的集合体系是JDK1.2才产生的。因此在JDK1.2之后,sun公司强行的让Vector实现了List接口。所以Vector内部出现了很多工程重复的方法。
2)什么是动态数组?
注意:Java中本质没有动态数组的,一旦数组的长度确定就不可改变(原因是因为数组是一段连续的内存地址),那为什么不设置一个逻辑连续,物理不连续?这样的数组是没有办法通过数组下标定位的。下标1万和找下标为0的速度是一样快的。因为他在内存中是连续的地址,只要在最开始的元素位置只要加上1万的4个字节就是4万个字节就你够立马找到。
动态数组的实现:一旦原来的数组空间不够时,创建一个长度更长的新数组,然后将旧的数组元素移动到新数组中,以此来实现数组的"动态扩容",旧的数组会因为没有引用,而被垃圾回收器回收掉
3)ArrayList源码解析
基本属性介绍
/**
* 默认的初始化容量
*/
private static final int DEFAULT_CAPACITY = 10;
/**
*
*/
private static final Object[] EMPTY_ELEMENTDATA = {};
/**
* 默认的空节点数组
*/
private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};
/**
* 底层的核心动态数组的引用
*/
transient Object[] elementData; // non-private to simplify nested class access
/**
* 数组的元素个数(不是数组的长度)
*/
private int size;构造方法
/**
有参构造方法。
参数为初始化数组的长度
*/
public ArrayList(int initialCapacity) {
if (initialCapacity > 0) {
//直接初始化指定长度的数组,赋值给elementData
this.elementData = new Object[initialCapacity];
} else if (initialCapacity == 0) {
this.elementData = EMPTY_ELEMENTDATA;
} else {
throw new IllegalArgumentException("Illegal Capacity: "+
initialCapacity);
}
}
/**
无参构造方法
*/
public ArrayList() {
//直接将默认的空数组赋值给elementData变量
this.elementData = DEFAULTCAPACITY_EMPTY_ELEMENTDATA;
}
疑问:为什么在两个构造方法给了不同的空数组?
因为从道理将给同一个是没有问题的,但是从设计角度来讲,这两个数组他会有一定的区别,一个是当数组参数零也就是指定了容量为0进行赋值空节点数组给elementData ,一个是默认参数为0赋值空节点数组给elementData,这个版本来看作用是同一个,但是当以后版本出现了变化是当数组参数零给的是进行列外一个操作这样DEFAULTCAPACITY_EMPTY_ELEMENTDATA和EMPTY_ELEMENTDATA就互不影响了。就是为了以后的扩展
元素添加(add)
/**
添加元素
*/
public boolean add(E e) {
//判断是否容量足够,如果不够就需要扩容
ensureCapacityInternal(size + 1);
//将元素e放入底层数组,下标为size的位置,然后size自增
elementData[size++] = e;
return true;
}
/**
容量判断
参数:本次至少需要的容量大小
*/
private void ensureCapacityInternal(int minCapacity) {
ensureExplicitCapacity(calculateCapacity(elementData, minCapacity));
}
/**
重新计算数组需要的长度,如果是第一次添加元素,则返回默认长度10
*/
private static int calculateCapacity(Object[] elementData, int minCapacity) {
if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
return Math.max(DEFAULT_CAPACITY, minCapacity);
}
return minCapacity;
}
/**
判断是否需要扩容
*/
private void ensureExplicitCapacity(int minCapacity) {
modCount++;
// 如果需要的最小容量超过了底层数组的实际长度,则进行扩容
if (minCapacity - elementData.length > 0)
//扩容方法
grow(minCapacity);
}
/**
数组扩容的方法
参数:为至少需要的容量大小
*/
private void grow(int minCapacity) {
//旧的容量
int oldCapacity = elementData.length;
//新的容量(按照原容量1.5倍扩容),右移一位相当于除以二,左移一位相当于乘以二
int newCapacity = oldCapacity + (oldCapacity >> 1);
//扩容的容量如果没有达到最小容量
if (newCapacity - minCapacity < 0)
//直接将最小容量变成新容量
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
//重要:数组扩容的方式
//copyOf - 将参数1的数组元素,拷贝到一个新数组中,新数组的容量为参数2,并且将新数组返回
elementData = Arrays.copyOf(elementData, newCapacity);
}
注意:copyOf底层是有native本地方法实现的,Java所有的native方法都是调用c/c++实现的
元素插入方法(add)
/**
将元素e插入到index位置
*/
public void add(int index, E element) {
//检测index是否越界
rangeCheckForAdd(index);
//检测是否需要扩容
ensureCapacityInternal(size + 1);
//参数1的数组,从参数2的位置开始
//复制到参数3的数组中,从参数3的参数4的位置开始设置,
//复制的元素总长度为参数5
System.arraycopy(elementData, index, elementData, index + 1,
size - index);
//将元素覆盖到index位置
elementData[index] = element;
//元素总数量加1
size++;
}获取元素(get)
public E get(int index) {
//检查下标越界
rangeCheck(index);
//获得下标index处的元素
return elementData(index);
}
作业:自行查看remove方法的源码
1.1.2 LinkedList
1)底层实现特点
特点:元素有序且可重复
底层实现:双向链表
2)什么是双向链表?
链表在内存中不是一串连续的地址,由一个一个节点组成,每个节点可以分为3部分(数据部分,头指针,尾指针)
优势:从中间插入和中间删除,只需要移动节点的指针指向,无需移动节点的位置
缺点:查询一个元素时,必须从头/尾依次往后/往前遍历
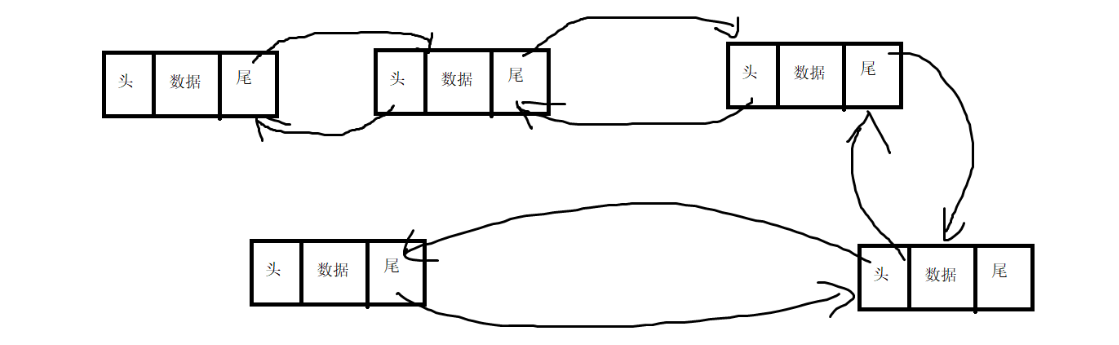
如何用Java代码实现一个双向链表?
//双向链表的节点对象
private static class Node<E> {
E item;
Node<E> next;
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
3)LinkedList的源码解析
常用的变量
//元素的个数/链表的节点数
transient int size = 0;
//指向双向链表头指针的引用
transient Node<E> first;
//指向双向链表尾指针的引用
transient Node<E> last;疑问为什么要做双向链表头指针和尾指针的引用?
因为没有这两个变量都找不到双向链表
添加元素的方法(add)
//添加元素
public boolean add(E e) {
linkLast(e);
return true;
}
//添加元素到链表的末尾
void linkLast(E e) {
//让l变量指向last所指向的最后一个节点
final Node<E> l = last;
//创建一个新的节点,数据部分就是新增的元素
//让新节点的头指针指向l
final Node<E> newNode = new Node<>(l, e, null);
//将新节点赋值给last
last = newNode;
//判断当前是否添加的第一个元素
if (l == null)
//如果是第一个元素,那么newNode也要赋值给first
first = newNode;
else
//如果不是,
l.next = newNode;
//元素个数++
size++;
modCount++;
}插入元素(add)
//插入元素到index的位置
public void add(int index, E element) {
//检查下标是否越界
checkPositionIndex(index);
//判断index是否在末端
if (index == size)
//尾部的追加
linkLast(element);
else
//插入
//参数1:插入的元素
//参数2:index位置的现有节点
linkBefore(element, node(index));
}
//获得index位置的元素
Node<E> node(int index) {
if (index < (size >> 1)) {
//查找的元素在前半段,从头开始依次往后变量
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
//查找的元素在后半段,从尾开始依次往前遍历
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
//将元素e,插入到节点succ的前面
void linkBefore(E e, Node<E> succ) {
//succ的当前节点的上一个节点的指针的对象赋值给pred
final Node<E> pred = succ.prev;
//创建出一个新的节点,e代表元素部分,pred指向上一个节点,succ指向下一个节点
final Node<E> newNode = new Node<>(pred, e, succ);
//这个新的节点又指向succ的上一个指针(说明原先succ不指向上一个指针了而转向指向这个新的节点)
succ.prev = newNode;
//如果pred == null这就说明了succ是第一个节点,
if (pred == null)
//那么newNode就是第一个节点
first = newNode;
else
//新节点指向了pred指向的下一个的指针
pred.next = newNode;
size++;
modCount++;
}
获得元素(get)
public E get(int index) {
//下标越界
checkElementIndex(index);
//获得index位置的节点,方式同上,再返回节点的数据部分
return node(index).item;
}
作业:自行查看remove方法的实现
1.1.3 ArrayList VS LinkedList性能分析
ArrayList查询速度很快,往中间插入/移除元素很慢。 LinkedList往中间插入/移除元素很快,查询元素很慢。
不确切
性能对比
插入性能对比: 尾部:ArrayList和LinkedList性能差异不大,几乎一样 头部:LinkedList性能 远远大于ArrayList性能,因为ArrayList需要进行数组的扩容 + 元素的位移(已经通过C优化) 中间:ArrayList性能 大于 LinkedList性能,原因在于LinkedList在插入中间位置时,需要查询中间的元素,LinkedList查询中间元素是最忙的操作
读取性能对比: ArrayList:读取任何位置性能差异不大,速度很快 LinkedList:读取越靠中间的元素,性能越差,越靠两边,性能越好(ArrayList性能差不多)
1.1.4 HashSet、LinkedHashSet、TreeSet
1)特点
HashSet:无序,不可重复 LinkedHashSet:不可重复,有序(插入顺序) TreeSet:不可重复,有序(字典序)
2)底层实现
Set集合的底层实现都是由Map集合实现的
1.2 Map体系
1.2.1 HashMap & Hashtable
1)底层实现和特点
HashMap和Hashtable底层都是由哈希表实现,HashMap和Hashtable的关系与ArrayList和Vector的关系是一样的。HashMap线程不安全,Hashtable线程安全。
特点:HashMap的key无序不可重复,value可以重复
2)哈希表的介绍
什么是哈希表?
哈希表是一种用于快速查询的数据结构,在精准定位方面性能非常的好(通过key找value),查找速度和元素的个数无关(理想状态,实际过程中,多少还是有点关系),时间复杂度为O(1)
优势:可以快速的通过key找到value。 快速定位、大数据去重、判断是否存在.... 哈希表???
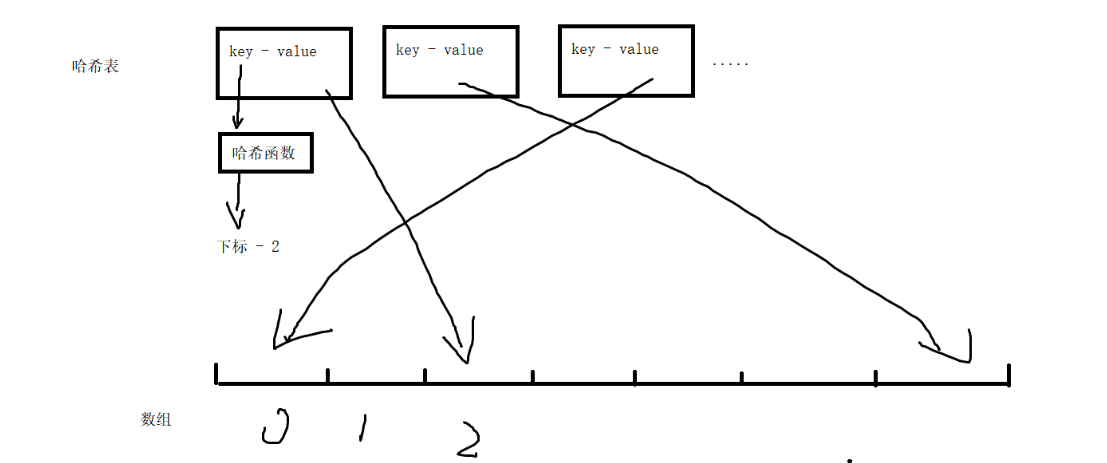
哈希表的底层是一个位数组?他是通过哈希函数转换成下标随机匹配坐标。这就导致了同一个位置可能会有重复元素,那么这个key有不一样怎么可能会相同呢因为哈希函数实现了key.hashcode() % array.length**不是按key实现的。这就导致哈希碰撞
什么是哈希函数?
可以将任意类型的key转换成int类型下标
特点: 1、任何类型 -> int类型 2、同一个值 在 任何时候,转换的下标必须一样 3、转成的下标必须落在哈希表的有效范围之内
自己实现一个哈希函数? 实现:key.hashcode() % array.length
什么是哈希碰撞?(哈希冲突 - 重要)
两个元素(key-value),通过哈希函数计算出同一个下标,如果key相同,则后面的元素value覆盖前面的元素value,如果key不同,则发生了所谓的哈希碰撞。哈希碰撞不是好事,而是因为不可避免。
问题1:哈希表是如何判断key是否相同的?
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
先判断两个key的hash值是否相同,如果相同,再判断两个元素的key是否相等(== 或者 equals)问题2:哈希碰撞发生后该怎么办?
哈希冲突的解决
1、开发地址法 - 发生碰撞后,新的元素自动往后移位 2、链地址法 - 将发生碰撞的元素通过链表连接起来(优势,不占其他的桶,劣势,影响查询性能)
注意:JDK1.8之后,引入了链表 + 红黑树的方式解决哈希冲突
哈希表的扩容
为什么哈希表要扩容? 随着添加元素越来越多,适当的扩容可以降低发生哈希碰撞概率。以及重新计算原来节点的桶位置,打散原来链表的长度,起到提高查询效率的作用。
扩容阈值:当元素个数达到扩容阈值之后,就会触发一次哈希表的扩容。 填充因子:扩容的元素比例,扩容阈值 = 哈希表容量 * 填充因子
3)红-黑树 - (简单介绍)
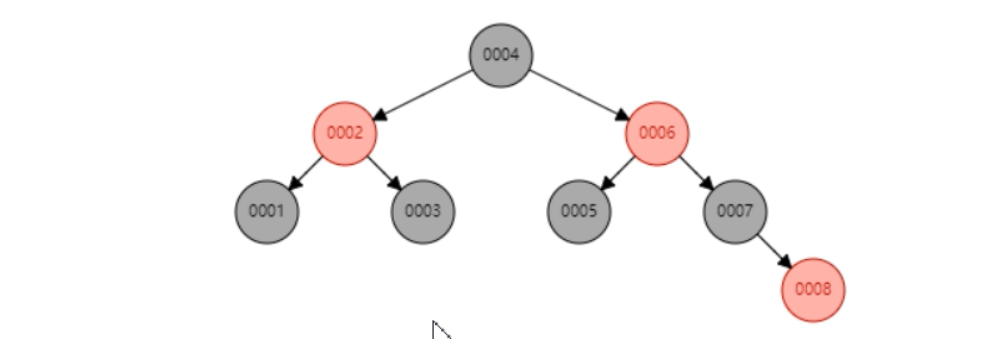
什么是红-黑树?
红-黑树是一种特殊的二叉搜索树,也是一种便于快速查询的数据结构,但是查询性能会比哈希表略低。
什么是二叉搜索树?
二叉树 -> 二叉搜索树。在二叉搜索树中,任何一个节点的所有左子节点都小于该节点,所有的右子节点都大于该节点,这种二叉树,就称之为二叉搜索树。
缺点:害怕树的失衡
红-黑树就是一个永远平衡的二叉搜索树
红黑规则
只要遵循了红黑规则的二叉搜索树就一定是平衡的 1、根节点一定是黑色 2、红色节点不能有红色的子节点(红红冲突) 3、从根节点触发,到任意一个叶子节点,经过的黑节点数量必须相同 4、新增的节点默认为红节点
红黑树的平衡手段
变色 + 旋转
4)HashMap源码解析 - JDK1.8
常用属性
/**
* 哈希表的默认初始长度 - 16(2的4次方)
*/
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
/**
* 哈希表的最大长度 - 2^30
*/
static final int MAXIMUM_CAPACITY = 1 << 30;
/**
* 默认填充因子 - 0.75
*/
static final float DEFAULT_LOAD_FACTOR = 0.75f;
/**
* 链表长度到8时转成红黑树
*/
static final int TREEIFY_THRESHOLD = 8;
/**
* 红黑树的个数到6时转成链表
*/
static final int UNTREEIFY_THRESHOLD = 6;
/**
* 哈希表的元素达到64时,链表才会转红黑树
*/
static final int MIN_TREEIFY_CAPACITY = 64;
/**
底层哈希表
*/
transient Node<K,V>[] table;
/**
当前的拓展阈值,当元素个数达到这个值时,就触发扩容
*/
int threshold;
/**
当前的填充因子
*/
final float loadFactor;哈希表中的节点元素
//哈希表的节点
static class Node<K,V> implements Map.Entry<K,V> {
final int hash; //当前节点的hash值,通过key计算而来
final K key; //key
V value;//值
Node<K,V> next;//下个节点的引用
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}构造方法
/**
* 无参构造
*/
public HashMap() {
//设置当前的填充因子为默认的填充因子 0.75f
this.loadFactor = DEFAULT_LOAD_FACTOR;
}
/**
有参构造
参数1:初始化的哈希表的长度
参数2:填充因子
*/
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
//1 2 4 8 16 32 64 128 ......
//根据初始容量,计算离这个容量最近的2的N次方的结果值
//设置给当前的扩容阈值
this.threshold = tableSizeFor(initialCapacity);
}
注意:JDK1.8之后,哈希表的容量必须是2的N次方
添加元素(put)
/**
添加元素
参数4:false代表,key相同时,value覆盖,如果为true,表示value不覆盖
*/
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
/**
哈希函数
*/
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
/**
核心的添加元素的方法
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
//tab - 代表当前的哈希表
//p - 代表当前key对应的哈希桶中的元素
//n - 代表哈希表的长度
//i - 代表key对应的哈希桶的下标
Node<K,V>[] tab; Node<K,V> p; int n, i;
//------------------第一次添加元素时触发-----------------------
//判断哈希表是否为空,如果为空表示当前第一次添加元素(table是)
if ((tab = table) == null || (n = tab.length) == 0)
//如果哈希表还没有初始化,就调用resize方法初始化哈希表
n = (tab = resize()).length;
//------------------第一次添加元素时触发-----------------------
//任何一个数字 & n 结果一定是0 ~ n范围
//(n - 1) & hash 通过key的哈希值计算下标,赋值给i
//从哈希表tab,下标为i的元素赋值给p
//判断p是否为null
if ((p = tab[i = (n - 1) & hash]) == null)
//说明当前哈希桶为空,没有发生哈希碰撞
//新建一个Node,将key,value等都保存到节点中
//将新的节点放入桶i的位置
tab[i] = newNode(hash, key, value, null);
else {
//桶i的位置不为空
//e - 哈希碰撞的桶的第一个元素
//k - 下标为i的哈希桶的第一个元素的key值
Node<K,V> e; K k;
//判断新增的key和p是否相同
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
//如果相等 将p赋值给e
e = p;
else if (p instanceof TreeNode)
//判断当前哈希桶中是否为红黑树
//走红黑树的逻辑
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
//哈希桶中是链表,并且发生了哈希碰撞
//遍历当前的桶的链表
for (int binCount = 0; ; ++binCount) {
//e一直指向p的下一个节点
if ((e = p.next) == null) {
//表示走到了最后一个节点,说明整个链表都没有发现相等的key
//创建一个新的节点,放入链表的尾端
p.next = newNode(hash, key, value, null);
//binCount - 循环的链表数量
//判断链表的长度是否达到转树的条件(有没有超过8)
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
//可能转红黑树???
treeifyBin(tab, hash);
break;
}
//判断节点e是否和添加的元素key相等
if (e.hash == hash &&
((k = 
