hdu 4272 LianLianKan 状态压缩

 

LianLianKan

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3681    Accepted Submission(s): 1101

Problem Description

I like playing game with my friend, although sometimes looks pretty naive. Today I invent a new game called LianLianKan. The game is about playing on a number stack.
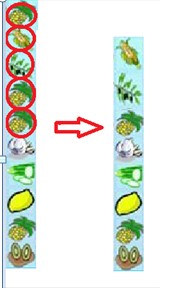
Now we have a number stack, and we should link and pop the same element pairs from top to bottom. Each time, you can just link the top element with one same-value element. After pop them from stack, all left elements will fall down. Although the game seems to be interesting, it's really naive indeed. 

To prove I am a wisdom among my friend, I add an additional rule to the game: for each top element, it can just link with the same-value element whose distance is less than 6 with it. 
Before the game, I want to check whether I have a solution to pop all elements in the stack.

 

 

Input

There are multiple test cases.
The first line is an integer N indicating the number of elements in the stack initially. (1 <= N <= 1000)
The next line contains N integer ai indicating the elements from bottom to top. (0 <= ai <= 2,000,000,000)

 

 

Output

For each test case, output “1” if I can pop all elements; otherwise output “0”.

 

 

Sample Input

2 1 1 3 1 1 1 2 1000000 1

 

 

Sample Output

 

1 0 0

http://acm.hdu.edu.cn/showproblem.php?pid=4272

题意：

 

题意：长度为n（n<=1000）的栈，栈顶元素可以与下面1~5个数中相同的元素消去，问最后能都完全消去。

题解：

 

状态压缩 dp  如何判断一个 物品 是否可以 被删除 ，首先 最坏的 情况是  2 0 0 0 0  1 1 1 1 2   假如我们要消除 栈顶的 2  ，0表示已经被删除了。

辅助解释：假设2前面有一个3，那么3能够消除的最远位置为最后一个0处；

我们要 知道 包括 本身在内的  10 个 数位 

定义dp[h][i]表示高度为h，状态为i时能否全部消除； 二进制位1表示未消除，0表示当前位已消除；

/**

定义dp[h][i]表示高度为h，状态为i时能否全部消除； 二进制位1表示未消除，0表示当前位已消除；

 

*/

#include<iostream>

#include<cstring>

#include<cstdio>

#include<string>

#include<set>

#include<algorithm>

#include<vector>

#include<map>

#include<queue>

#include<cmath>

#include<cctype>

#include<stack>

#include<iomanip>

using namespace std;

const int maxn = 1200;

int dp[maxn][maxn];

int a[maxn];

int dfs(int h,int c)

{

    if(h < 0){

        if(c) return 0;// 

        else return 1;// 结果为0，表明可以完全消除；

    }

    if(dp[h][c]!=-1) return dp[h][c];

    int &res = dp[h][c];

    res = 0;

    int t = c&(1<<9);//获得定点的位，以判断是否已经被消除；

    if(t){//未被消除；

        c = c^(1<<9);//把顶去掉；

        int cnt = 0;

        for(int i = 1,j = 8;i <= 9&&j>=0; i++,j--){

            if(c&(1<<j)){//如果当前位置未去掉；

                cnt++;

                if(cnt>5) break;//控制距离小于6；

                if(a[h] == a[h-i]){//如果和顶相等；去掉当前位；

                    int t = c^(1<<j);

                    t <<= 1;

                    if(h-10>=0) t += 1;

                    res = dfs(h-1,t);

              //      else res = dfs(h-1,t);

                    if(res) break;

                }

            }

        }

    }else

    {//已经被消除时，脱栈顶；

        c <<= 1;

        if(h-10>=0) res = dfs(h-1,c+1);//h>=10表明可以继续下移；

        else res = dfs(h-1,c);

    }

    return res;

}

int main()

{

    int n;

    while(scanf("%d",&n)==1)

    {

        for(int i = 0; i < n; i++){

            scanf("%d",&a[i]);

        }

        if(n%2){//数量为奇数个，肯定不可以一一配对完全消除；

            printf("0\n"); continue;

        }

        memset(dp,-1,sizeof dp);

        int c = 0, i, j;

        for(i = n-1, j = 0; i >= 0&&j<=9; i--,j++){//初始化二进制111111111；

            c = (c<<1)+1;

        }

        while(j<=9){//n<9时，补0；只是为了方便同一处理；

            c <<= 1;

            j++;

        }

        printf("%d\n",dfs(n-1,c));

    }

    return 0;

}