直角三角锥

链接：https://www.nowcoder.com/acm/contest/81/A
来源：牛客网
在三维空间中，平面 x = 0, y = 0, z = 0，以及平面 x + y + z = K 围成了一个三棱锥

整天与整数打交道的小明希望知道这个三棱锥内、上整点的数目。

他觉得数量可能很多，所以答案需要对给定的 M 取模。

输入描述:

输入有 1 ≤ T ≤ 1e5 组数据，每组数据中，输入两个整数 0<=k<=1e9+7,0<=m<=1e9+7,意义如题目描述。

输出描述:

对于每组数据，输出一个整数，为三棱锥内、上整点的数目对 M 取模。

输入

4
0 60
1 60
29 60
29 100007

输出

1
4
40
4960

解法

这道题目公式都已经推出来了，但是却没有化简，最后还是没有做出来。

这道题目我将它当做一个排列组合问题来思考，它相当于是要寻找x+y+z<=k && x>=0 && y>=0 && z>=0 的整点数个数，其实满足这个条件的数，就相当于寻找x+y+z<=k-1 && x>=0 && y>=0 && z>=0 和 x+y+z=k && x>=0 && y>=0 && z>=0这两个区域数的个数，那么我们只需要解决x+y+z=k && x>=0 && y>=0 && z>=0这个子问题，再进行累加求和就行了。

对于x+y+z=k && x>=0 && y>=0 && z>=0这个区域，整数的个数又有多少呢，其实固定其中x,y的取值，z的取值就会得到，当x取0，y有k+1取法，当x取1，y有k种取法。。

所以总数=(k+1)+k+(k-1)+......+2+1=(k+2)*(k+1)/2

推出得到公式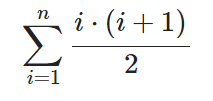这个n=k+1,然后进行化简，之前我想复杂了，我将第i项和第i+1项结合起来，并分了奇偶来做，其实将括号打开就行，最后化简得到

(n+1)*(n+2)*(n+3)/6,这道题目还涉及如何取模，当(n+1)*(n+2)*(n+3)相乘，范围可能会爆掉，所以要在之前取模，而取模可能会影响到除法的操作，m*=6，就会使最后结果不变。

#include<iostream>
using namespace std;


int main(){
    int t;
    cin >> t;
    while (t--){
        long long k, m;
        cin >> k >> m;
        m *= 6;
        cout<< (k + 1)*(k + 2)%m*(k + 3)%m / 6 <<endl;
    }
}