二叉树介绍

常见二叉树有完全二叉树、满二叉树

满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。 --来自百度百科

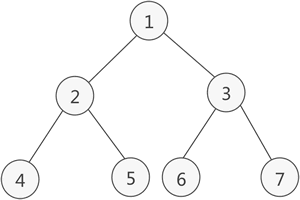
满二叉树除了满足普通二叉树的性质，还具有以下性质：

1.满二叉树中第 i 层的节点数为 2^n-1 个。

2.深度为 k 的满二叉树必有 2^k-1 个节点，叶子数为 2^k-1。

3.满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。

4.具有 n 个节点的满二叉树的深度为 log₂(n+1)。

完全二叉树：如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

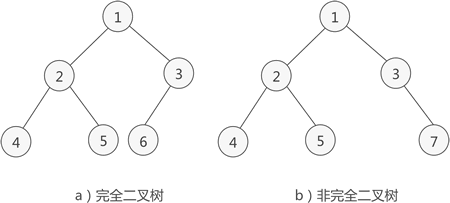
二叉树的遍历方式：

前序遍历：中左右

中序遍历：左中右

后续遍历：左右中

即以中间节点的位置来定义

以下图为例：

前序遍历：1245367

即先中间的根节点，此时为1；然后是左边的节点（245），依次遍历为左边节点的2，然后继续左边的节点4，左边没有节点后再右边节点5；当整个左边都遍历后再遍历右边的节点（367），依次遍历右边节点3，然后遍历右边的左节点6，当右边的左节点遍历完成后再遍历右边的右节点7

中序遍历：4251637

按照之前的定义，先遍历左边，左边先遍历左节点4 、2 ，左边的左节点遍历完成后再遍历左边的右节点5；左边遍历完成后遍历中间即根节点1；中间遍历完成后遍历右边，先遍历右边的左节点即6、3，右边的左节点遍历完成后再遍历右边的右节点7

后序遍历：4526731

遍历顺序先左右再中，首先遍历左边的左右节点4 、5，左右遍历完成后遍历中2，左边遍历完成后遍历右边；先右边的左右节点 6、7，再遍历中3，右边节点遍历完成后在遍历中节点即根节点1

代码实现

前序遍历

def preorderTraversal(root):
    ans = []
    def traversal(root):
          if root == None:
              return
          ans.append(root.val) # 中
          traversal(root.left)    # 左
          traversal(root.right)   # 右
    traversal(root)
    return result

中序遍历

def inorderTraversal(root):
      ans= []
      def traversal(root):
            if root == None:
                return
            traversal(root.left)    # 左
            ans.append(root.val) # 中
            traversal(root.right)   # 右
      traversal(root)
      return result

后序遍历

def postorderTraversal(root):
      result = []
      def traversal(root):
            if root == None:
                return
            traversal(root.left)    # 左
            traversal(root.right)   # 右
            result.append(root.val) # 中
      traversal(root)
      return result