基础算法-快速排序

  基本思想-分治

1.确定分界点：q[l],q[(l+r)/2],q[r],随机。

2.调整区间：把<=x的数据放在左部分，把>=x的数据放在右部分。

3.递归处理左右两部分。

 

其中第2步“调整区间”：

设两个指针i、j，指针i从l往r走，遇到>=x的就停止；指针j从r往l走，遇到<=x的就停止；此时再将两指针所指内容交换，各取所需。

因为任意时刻i左边的数据都是<x的，j右边的数据都是>x的,所以当i和j这两个指针相遇或j大于i即排序结束。

 

排序算法代码如下：

#include <iostream>
using namespace std;

void quick_sort(int q[],int l,int r)
{
   int x=q[(l+r)/2],i=l-1,j=r+1;//由于是先移动再判断 ，为了能与边界的值比较
   if(l>=r) return;
   

   while(i<j)
   {
   	 do i++;while (q[i]<x);
   	 do j--;while (q[j]>x);
   	 if(i<j) swap(q[i],q[j]); 
	} 
	
	quick_sort(q,l,j);
	quick_sort(q,j+1,r);	
	
 } 
 
 int main()
 {
 	int n;
    scanf("%d",&n);
    int* q = new int[n];  // 堆上分配
 	for(int i=0;i<n;i++) scanf("%d",&q[i]);
 	
 	quick_sort(q,0,n-1);
 	
 	for(int i=0;i<n;i++) printf("%d ",q[i]);
 	
 	return 0;
 }

tip:

当q[l]作为基准值(x),j从右向左找 ≤ x 的元素,j右边的元素都是 ≥ x 的（可靠）,j本身指向的元素是 ≤ x 的,所以递归分界用j

quick_sort(q, l, j);      // j在左半部分
quick_sort(q, j + 1, r);  // j+1开始是右半部分

当q[r]作为基准值(x),i从左向右找 ≥ x 的元素,i左边的元素都是 ≤ x 的（可靠）,i本身指向的元素是 ≥ x 的,所以递归分界用i

quick_sort(q, l, i - 1);  // i-1结束是左半部分
quick_sort(q, i, r);      // i开始是右半部分

分界点是中点q[(l+r)/2]时,建议递归分界用j。

效率分析：

 

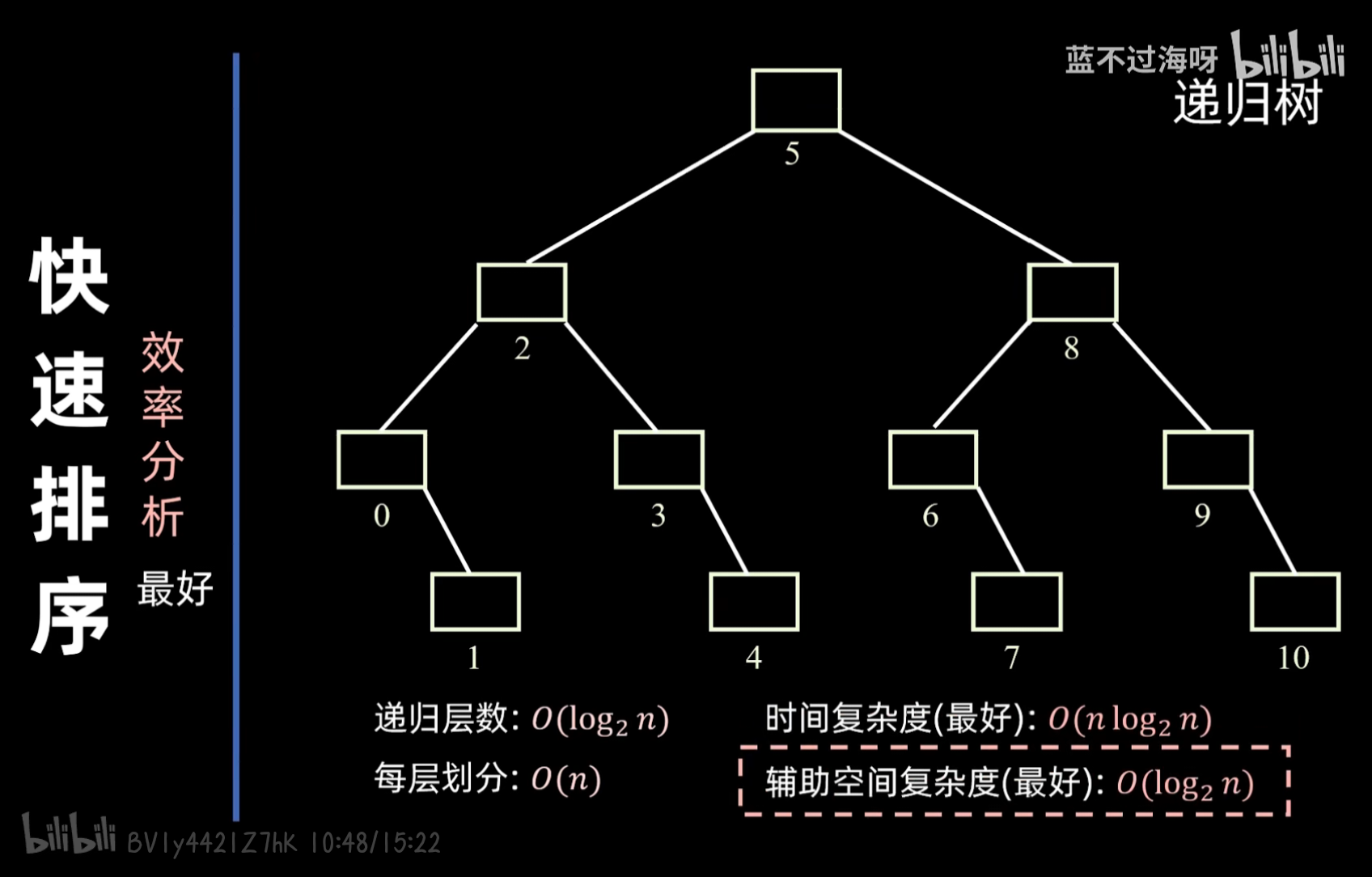
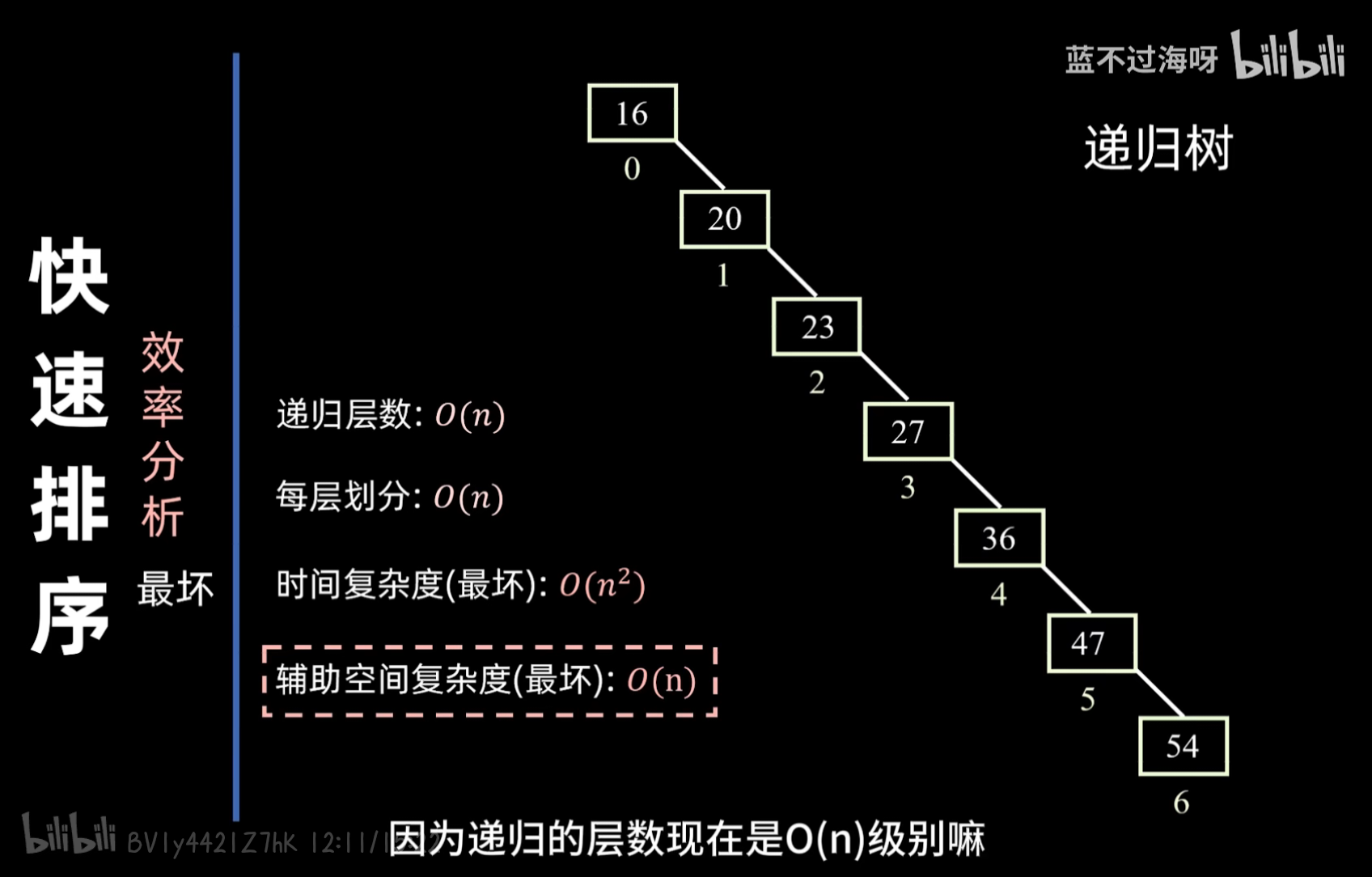
补充说明：时间和空间复杂度的好坏取决于选取的分界点，若选取的分界点恰好能将数组一分为二，则为最好情况；选取的分界点为数组中的最值，则为最坏情况。quick_sort中虽然是常数个变量（q是一个数组指针，但它不占用递归栈上的额外空间来存储数组本身)，但是其包含递归，递归的层数就是其空间复杂度。

快速排序是不稳定排序。

快速选择算法

给定一个长度为 n 的整数数列，以及一个整数 k，请用快速选择算法求出数列从小到大排序后的第 k 个数。

基本思想-选择一边递归

1.k<=Sl,递归左边。2.k>Sl,递归右边。

代码如下：

#include <iostream>
using namespace std;

int quick_select(int l,int r,int k,int q[])
{
	int x=q[(l+r)/2];int i=l-1;int j=r+1;
	if(l==r) return q[l];
	
	while(i<j)
	{
		do i++;while(q[i]<x);
		do j--;while(q[j]>x);
		if(i<j) swap(q[i],q[j]);
		
	}
	int sl=j-l+1; 
	if(k<=sl) return quick_select(l,j,k,q);
	else return quick_select(j+1,r,k-sl,q);
}

int main()
{
	int n;int k;
	cin>>n>>k;
	int*q=new int[n];
	for(int i=0;i<n;i++)
	cin>>q[i];
	
	cout<<quick_select(0,n-1,k,q);
	
	return 0;
}

时间复杂度=n+n/2+n/4+n/8+...=O(n)