day2021_10_05

今日内容

• 完成概率图模型以及强化学习的重点复习

  • \(\epsilon\)-贪心：基于一个概率来对探索和利用进行折中：每次尝试时，以\(\epsilon\)的概率进行探索，以均匀概率随机选取一个摇臂，以1-\(\epsilon\)的概率进行利用，即选择当前平均奖赏最高的摇臂

  

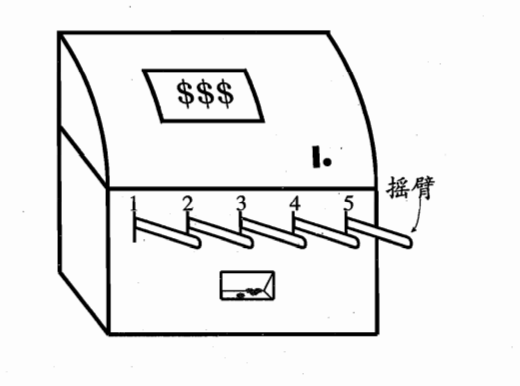
  比如图上有五个摇臂，有100次摇臂的机会，

  当进行第1次摇臂时，此时收益\(Q_0=0\)，随机产生一个\([0,1]\)的随机数，如果小于\(\epsilon\)，则从1-5号机中以相同概率随机选取一个摇臂开始摇，如果大于\(\epsilon\)，则选择第0轮结束后，平均奖赏值最大的摇臂开始摇，显然一开始大家都是0，所以随机选一个。更新\(Q_1=\frac{Q_0*0+v_1}{0+1}\),其中\(v_1\)是选择某个摇臂后得到的奖惩。当我们尝试了12次，

  • 其中2次一号机，两次都赢得一块钱，则\(Q(1)=\frac{1+1}{2}=1\)

  • 2次二号机,一次1块，一次2块，则\(Q(2)=\frac{1+2}{2}=1.5\)

  • 3次三号机,两次1块，一次2块，则\(Q(3)=\frac{1+1+2}{3}=1.33\)

  • 2次四号机，一次一块，一次没钱，则\(Q(4)=\frac{1+0}{2}=0.5\)

  • 3次五号机，两次一块，一次2块\(Q(5)=\frac{1+1+2}{2}=1.33\)

  当进行第13次摇臂时，此时收益为\(Q_{13}\)，随机产生一个\([0,1]\)的随机数，如果小于\(\epsilon\)，则从1-5号机中以相同概率随机选取一个摇臂开始摇，如果大于\(\epsilon\)，则选择第12轮结束后，平均奖赏值最大的摇臂开始摇，也就是二号机，更新\(Q_{13}=\frac{Q_{12}*12+v_13}{12+1}\),其中\(v_{13}\)是选择二号摇臂后得到的奖惩。如此进行到100次结束。

  • 显然选择当前平均效率最高的概率为\(1-\epsilon+\frac{\epsilon}{k}\),\(k\)为多少个摇臂。所以，\(\epsilon\)-贪婪意味着大多数时候都选择当前最佳选项（“贪婪”），但有时选择概率很小的随机选项。

  • 如果摇臂奖赏的不确定性比较大，就是概率分布比较宽时，则需要更多的探索，此时就需要较大的\(\epsilon\)的值；如果我们进行了多次的摇臂，可以很好的近似真实奖赏时，就可以让\(\epsilon\)的值小一点，进行更多的利用。

  • Q_learning与Sarsa算法的不同点：

    • Q-learning 在学习的时候，用的是贪婪的方法，所以学的一定是最大的。但是在选择的时候因为\(\epsilon\)而存在随机性，下一个更新的不一定是最大回报对应的行为n。但每次更新的回报一定是贪婪的，也就是最大Q的。

      Sarsa 在learn之前用\(\epsilon\)-贪婪选择了行为，并且确定用这个行为进行学习。所以学习的不一定是最大回报的。但学的跟做的是一样的。

所遇困难

• Q-leanring方法的执行策略有点头疼，到底是更新一步Q表后就执行到新的状态，还是尝试走完所有步后，更新Q表，再跟着Q表走，而且这时候还是\(\epsilon\)-贪婪策略走还是，直接贪婪策略走下一步。

明日计划

• 看下工程训练的需求文档能不能写一点。