数据结构(二)——排序

排序：稳定排序算法，不稳定排序算法

 

 

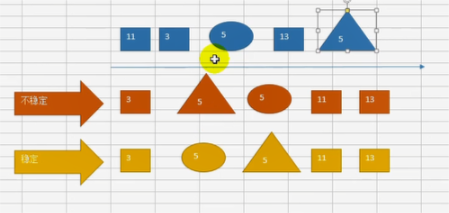
如上图，若两个5排序之后交换了位置就是不稳定的，没有交换位置就是稳定排序

 

1.选择排序

　　

 

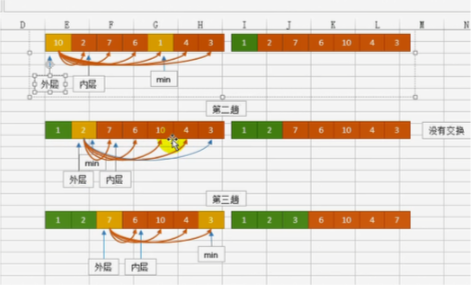
　　冒泡是相邻的两个交换，选择法是首元素与最小的交换。

void xuanzhepaixu(int* my_array, int len)
{
    for (int i = 0; i < len - 1; ++i) {
        for (int j = i + 1; j < len; ++j) {
            if (my_array[i] > my_array[j]) {// 交换次数多，不如记录下表位置效率高
                int temp = my_array[i];
                my_array[i] = my_array[j];
                my_array[j] = temp;
            }
        }

    }
}

 

 

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 选择法排序
void xuanzhepaixu(int* my_array, int len)
{
    int min = 0;
    for (int i = 0; i < len - 1; ++i) {
        min = i;
        for (int j = i + 1; j < len; ++j) {
            if (my_array[min] > my_array[j]) {
                min = j;// 保存最小元素的位置
            }
        }
        if ( min != i ) {
            int temp = my_array[i];
            my_array[i] = my_array[min];
            my_array[min] = temp;
        }
    }
}

void my_print_array(int* my_array, int len)
{
    for (int i = 0; i < len; ++i) {
        printf("%5d", my_array[i]);
    }
    printf("\n");
}

int main()
{
    int my_array[] = {10, 6, 7, 4, 9, 8, 5, 1, 3, 2};
    int len = sizeof(my_array) / sizeof(int);

    xuanzhepaixu(my_array, len);

    my_print_array(my_array, len);

    system("pause");
    return 0;
}

 

2.冒泡排序

 

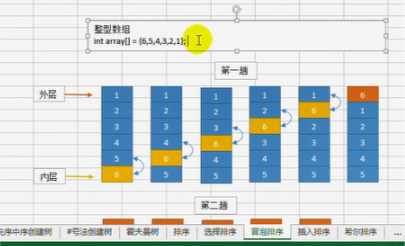
void maopaopaixu(int* my_array, int len)
{
    for (int i = 0; i < len; ++i) {
        for (int j = 1; j < len; ++j) {
            if ( my_array[j] > my_array[j - 1] ) {
                int temp = my_array[j];
                my_array[j] = my_array[j - 1];
                my_array[j - 1] = temp;
            }
        }
    }
}

 

冒泡算法的优化，在待排序数据处于一种趋于有序的情况，可以减少判断次数，比如：1，2，3，4，7，5，6

void maopaopaixu(int* my_array, int len)
{
    bool flag = false;
    for (int i = 0; i < len && !flag; ++i) {
        flag = true;
        for (int j = 1; j < len; ++j) {
            if ( my_array[j] > my_array[j - 1] ) {
                int temp = my_array[j];
                my_array[j] = my_array[j - 1];
                my_array[j - 1] = temp;
                flag = false;
            }
        }
    }
}

 

3.插入排序

　　默认对两个序列进行操作：有序序列，无序序列。

　　可以将无序序列分为两个部分

 

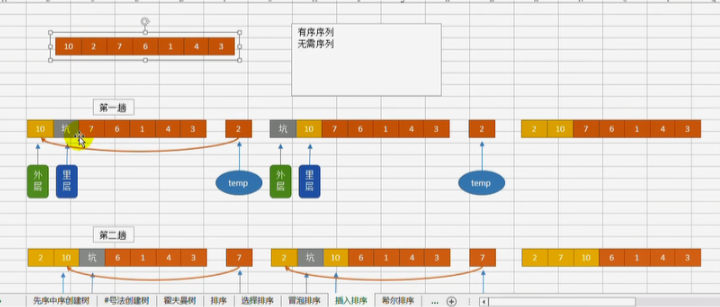
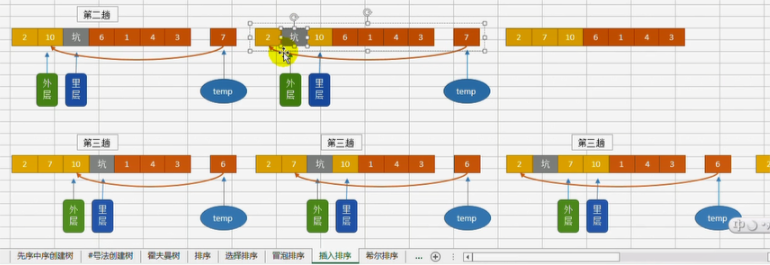
void insert_paixu(int* my_array, int len)
{
    int temp = 0;// 存储基准数
    int index = 0; // 存储坑的位置

    for (int i = 1; i < len; ++i) {
        temp = my_array[i];
        index = i;
        for (int j = i - 1; j >= 0; --j) {// 从后往前遍历
            if (temp < my_array[j]) {
                my_array[j + 1] = my_array[j];
                index = j;
            }
            else break;//最后一个保存的是最大的元素，此语句可以减少判断
        }
        my_array[index] = temp;
    }
}

 

4.希尔排序

　　先分组，再对每组进行插入排序。希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分为一组，算法便终止；

　　

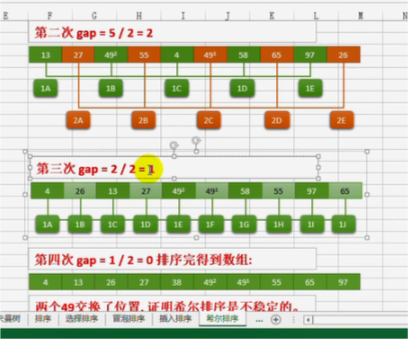
void shell_sort(int* my_array, int len)
{
    // 步长
    int gap = len;
    while (gap > 1) {
        // 步长递减公式，此步长下的希尔排序效率最高
        // 直到步长等于1
        gap = gap / 3 + 1;
        // 分组，对每一组进行插入排序
        for (int i = 0; i < gap; ++i) {
            // 插入排序
            int temp = 0;
            int index = 0;
            // 无序序列
            for (int j = i + gap; j < len; j += gap) {
                temp = my_array[j];
                index = j;
                // 有序序列(从后往前遍历)
                for (int k = j - gap; k >= 0; k -= gap) {
                    if (temp < my_array[k]) {
                        // 元素后移
                        my_array[k + gap] = my_array[k];
                        index = k;
                    }
                    else break;
                }
                my_array[index] = temp;// 填坑
            }
        }
    }
}

 

5.快速排序

　　快速排序 = 挖坑填数 + 分治法

　　分治法的思想：

　　　　1.先从数列中取出一个数作为基准数

　　　　2.分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边

　　　　3.再对左右区间重复第二步，直到各区间只有一个数

 

 

 

// 快速排序
void fast_sort(int* my_array, int left, int right)
{
    if (left >= right)
        return;
    int index = left, temp = 0;
    int i = left, j = right;
    temp = my_array[left];//基准位置
    while ( i < j ) {
        if (i == index) {
            if (my_array[j] < temp) {
                my_array[index] = my_array[j];
                index = j;
                ++i;
            }
            else --j;
        }
        if (j == index && i != j) {
            if (my_array[i] > temp) {
                my_array[index] = my_array[i];
                index = i;
                --j;
            }
            else ++i;
        }
    }
    my_array[i] = temp;
    fast_sort(my_array, left, i -1);
    fast_sort(my_array, i + 1, right);
    
}

 

void q_sort(int* my_array, int left, int right)
{
    if (left >= right)
        return;
    int i = left;// 开始位置
    int j = right;// 最后一个元素的位置
    int temp = my_array[left];//基准数
    while (i < j) {
        // j位置的元素，大于基准数
        while (i < j && my_array[j] >= temp) {
            // j 前移
            --j;
        }
        if (i < j) {
            my_array[i] = my_array[j];// 填坑
            ++i;
        }
        // 移动i
        while (i < j && my_array[i] <= temp) {
            ++i;
        }
        if (i < j) {
            my_array[j] = my_array[i];
            --j;
        }
    }
    my_array[i] = temp;//填坑
    q_sort(my_array, left, i -1);
    q_sort(my_array, i + 1, right);
}

 

6.归并排序

　　空间换时间的算法

　　将两个或两个以上的有序序列合并成一个新的有序序列：

　　　　有序序列V[1]...V[m]和V[m+1]...V[n] ===>V[1]...V[n]

 

void merge_array(int a[], int first, int mid, int last, int temp[])
{
    int i = first;// 第一个有序序列的开始下标
    int j = mid + 1;//第二个有序序列的开始下标
    int length = 0;
    // 开始合并
    while (i <= mid && j <= last) {
        // 找二者中比较小的数
        if (a[i] < a[j]) {
            temp[length] = a[i];
            ++i;
        }
        else {
            temp[length] = a[j];
            ++j;
        }
        ++length;
    }
    // 还剩下一个有序序列有元素
    while (i <= mid) {
        temp[length] = a[i];
        ++i;
        ++length;
    }
    while (j <= last) {
        temp[length++] = a[j++];
    }
    // 覆盖原来位置的无序序列
    for (int i = 0; i < length; ++i) {
        //找到原来的第一个有序序列的开始位置
        a[first + i] = temp[i];
    }
}

//归并排序
void merge_sort(int a[], int first, int last, int temp[])
{
    //递归结束条件
    if (first == last) {
        return;
    }
    // 从中间位置拆分
    int mid = (first + last) / 2;
    //拆分
    //左半边
    merge_sort(a, first, mid, temp);
    //右半边
    merge_sort(a, mid + 1, last, temp);
    //合并两个有序序列
    merge_array(a, first, mid, last, temp);
}

void my_print_array(int* my_array, int len)
{
    for (int i = 0; i < len; ++i) {
        printf("%5d", my_array[i]);
    }
    printf("\n");
}

int main()
{
    int my_array[] = {10, 6, 7, 4, 9, 8, 5, 1, 3, 2};
    int len = sizeof(my_array) / sizeof(int);
    int* temp = (int*)malloc(sizeof(my_array));
    merge_sort(my_array, 0, len -1, temp);
    free(temp);
    my_print_array(my_array, len);

    system("pause");
    return 0;
}

 

7.堆排序

构建一个堆（构建一个完全二叉树——存到数组中）：

　　1>大顶堆——根节点大于两个子节点（降序排列）

　　2>小顶堆——根节点小于两个子节点（升序排列）

操作：

　　根节点-1

　　左子树2i(i是父节点的序号)

　　右子树2i+1

（未完待续......）