【概率论与数理统计】第三章 多维随机变量及其分布(4)

3 两个随机变量的概率分布

3.1 两个离散型随机变量的函数的函数分布

例1：设二维随机变量\((X,Y)\)的分布律为：

X	Y	Y	Y
X	1	2	3
1	\(\frac{1}{4}\)	\(\frac{1}{6}\)	\(\frac{1}{8}\)
2	\(\frac{1}{4}\)	\(\frac{1}{8}\)	\(\frac{1}{12}\)

求：（1）\(Z_1 = X + Y\)的分布律；

（2）\(Z_2 = XY\)的分布律；

（3）\(P\{X = Y\}\)。

解：（1）\(Z_1\)可能的取值为\(\{1,2\} + \{1,2,3\} = \{2,3,4,5\}\)；

事件\(\{Z_1 = 2 \}\)的概率为：\(P\{Z_1 = 2\} = P\{X = 1, Y = 1\} = \frac{1}{4}\)；

事件\(\{Z_1 = 3 \}\)的概率为：\(P\{Z_1 = 3\} = P\{X = 1, Y = 2\} + P\{X=2, Y=1\} = \frac{5}{12}\)；

事件\(\{Z_1 = 4 \}\)的概率为：\(P\{Z_1 = 4\} = P\{X = 1, Y = 3\} + P\{X =2, Y =2\} = \frac{1}{4}\)；

事件\(\{Z_1 = 5 \}\)的概率为：\(P\{Z_1 = 5\} = P\{X = 2, Y = 3\} = \frac{1}{12}\)；

因此，\(Z_1 = X + Y\)的分布律为：

\(Z_1\)	2	3	4	5
P	\(\frac{1}{4}\)	\(\frac{5}{12}\)	\(\frac{1}{4}\)	\(\frac{1}{12}\)

（2）\(Z_2\)的取值可能为\(1,2,3,4,6\)概率分别为：

\(P\{Z_2 = 1\} = P\{X=1, Y=1\} = \frac{1}{4}\)

\(P\{Z_2 = 2\} = P\{X=1, Y=2\} + P\{X=2, Y=1\} = \frac{5}{12}\)

\(P\{Z_2 = 3\} = P\{X=1, Y=3\} = \frac{1}{8}\)

\(P\{Z_2 = 4\} = P\{X=2, Y=2\} = \frac{1}{8}\)

\(P\{Z_2 = 6\} = P\{X=2, Y=3\} = \frac{1}{12}\)

于是，\(Z_2 = XY\)的概率分布律为：

\(Z_2\)	1	2	3	4	5
P	\(\frac{1}{4}\)	\(\frac{5}{12}\)	\(\frac{1}{8}\)	\(\frac{1}{8}\)	\(\frac{1}{12}\)

（3）事件\(\{X = Y\} = \{X=1, Y =1\} \cup \{X=2, Y=2\}\)；因此：

\(P\{X = Y\} = P\{X=1, Y=1\} + P\{X=2, Y =2\} =\frac{3}{8}\)

例2：设二维随机变量\((X,Y)\)的分布律为：

X	Y	Y	Y
X	1	2	3
1	\(\frac{1}{5}\)	\(0\)	\(\frac{1}{5}\)
2	\(\frac{1}{5}\)	\(\frac{1}{5}\)	\(\frac{1}{5}\)

求：（1）\(Z=X-Y\)的分布律; （2）\(P\{X \lt Y\}\)

解：（1）\(Z\)可能的取值为\(\{0,-1,-2,1\}\)，概率分别为：

\(P\{Z = -2\} = P\{X = 1, Y=3\} = \frac{1}{5}\)

\(P\{Z = -1\} = P\{X =1,Y=2\} + P\{X=2,Y=3\} = \frac{1}{5}\)

\(P\{Z = 0\} = P\{X=1, Y =1\} + P\{X=2,Y=2\} = \frac{2}{5}\)

\(P\{Z=1\} = P\{X=2,Y=1\} = \frac{1}{5}\)

于是，\(Z=X-Y\)的分布律为：

Z	-2	-1	0	1
P	\(\frac{1}{5}\)	\(\frac{1}{5}\)	\(\frac{2}{5}\)	\(\frac{1}{5}\)

（2）事件\(\{X \lt Y\} = \{X=1,Y=2\} \cup \{X=1,Y=3\} \cup \{X=2, Y=3\}\)，所以：

\(P\{X \lt Y\} = P\{X=1,Y=2\} + P\{X=1,Y=3\} + P\{X=2, Y=3\} = \frac{2}{5}\)

也可以根据\(Z=X-Y\)的分布中\(Z \lt 0\)的概率得到：

\(P\{X \lt Y\} = P\{X - Y \lt 0\} = P\{X-Y = -2\} + \P\{X-Y = -1\} = \frac{2}{5}\)

例3：设随机变量\(X\)与\(Y\)相互独立，分别服从参数为\(\lambda_1,\ \lambda_2\)的泊松分布，证明：\(Z = X + Y\)服从参数为\(\lambda = \lambda_1 + \lambda_2\)的泊松分布。

证明：由已知得：

\(P\{X=k\} = \frac{\lambda_1^k e^{-\lambda_1}}{k!},\ \ P\{Y=k\} = \frac{\lambda_2^k e^{-\lambda_2}}{k!};\ \ k=0,1,2,...\)

事件\(\{Z=k\} = \{X=0,Y=k\} \cup \{X=1,Y=k-1\} \cup ... \cup \{X=k,Y=0\}\)则：

\(P\{Z=k\} = P\{X=0,Y=k\} + P\{X=1,Y=k-1\} + ... + P\{X=k,Y=0\} = \sum_{i=0}^{k} P\{X=i, Y=k-i\}\)

因为\(X\)与\(Y\)相互独立，所以：

\(P\{X=i,Y=k-i\} = P\{X=i\} \cdot P\{Y=k-i\}\) 因此：

\[\begin{align} P\{Z=k\} &= \sum_{i=0}^{k} P\{X=i\} \cdot P\{Y=k-i\} \\ &= \sum_{i=0}^{k} \frac{\lambda_1^i e^{-\lambda_1}}{i!} \cdot \frac{\lambda_2^{k-i} e^{-\lambda_2}}{(k-i)!} \\ &= \sum_{i=0}^{k} \frac{\lambda_1^i e^{-\lambda_1}}{i!} \cdot \frac{\lambda_2^{k-i} e^{-\lambda_2}}{(k-i)!} \cdot \frac{k!}{k!} \\ &= e^{-(\lambda_1 + \lambda_2)} \cdot \frac{1}{k!} \cdot \sum_{i=0}^{k} \frac{k!}{i!(k-i)!} \lambda_1^i \lambda_2^{k-i} \\ &= e^{-(\lambda_1 + \lambda_2)} \cdot \frac{1}{k!} \cdot \sum_{i=0}^{k} C_k^i \lambda_1^i \lambda_2^{k-i} \\ &= \frac{ e^{-(\lambda_1 + \lambda_2)} (\lambda_1 + \lambda_2)^k }{k!} \ \ \ \ \ \ \ \ ,k=0,1,2,... \\ &= \frac{ e^{-\lambda} \lambda^k }{k!} \ \ \ \ \ \ \ \ ,k=0,1,2,... \end{align} \]

因此，\(Z = X + Y\)服从参数为\(\lambda = \lambda_1 + \lambda_2\)的泊松分布。

3.2 两个相互独立的连续型随机变量之和的概率分布

例4：设\(X\)与\(Y\)是两个相互独立的连续型随机变量，\(X\)在\([0,1]\)上服从均匀分布，\(Y\)的概率密度为：

\[f_Y(y) = \begin{cases} \frac{1}{2} e^{\frac{1}{2} y},\ \ \ \ \ \ \ \ &y \gt 0 \\ 0,\ \ \ \ \ \ \ \ &y \le 0 \end{cases} \]

求：（1）\((X,Y)\)的概率密度；（2）\(P\{X+Y \le 1\}\)；（3）\(P\{X+Y \le 3\}\)。

解：（1）由于\(X\)服从均匀分布，所以\(X\)的概率密度为：

\[\begin{align} f_X(x) &= \begin{cases} \frac{1}{1-0} ,\ \ \ \ \ \ \ \ &0 \le x \le 1 \\ 0,\ \ \ \ \ \ \ \ &其他 \end{cases} \\ &= \begin{cases} 1,\ \ \ \ \ \ \ \ \ \ \ \ \ &0 \le x \le 1 \\ 0,\ \ \ \ \ \ \ \ \ \ \ \ \ &其他 \end{cases} \end{align} \]

又因为\(X\)与\(Y\)相互独立，所以\((X,Y)\)的概率密度为：

\[f(x,y) = f_X(x) \cdot f_Y(y) = \begin{cases} \frac{1}{2} e^{-\frac{1}{2}y} ,\ \ \ \ &0 \le x \le 1, y \gt 0\\ 0, &其他 \end{cases} \]

（2）利用(1)的结果；并画出二重积分的图像：

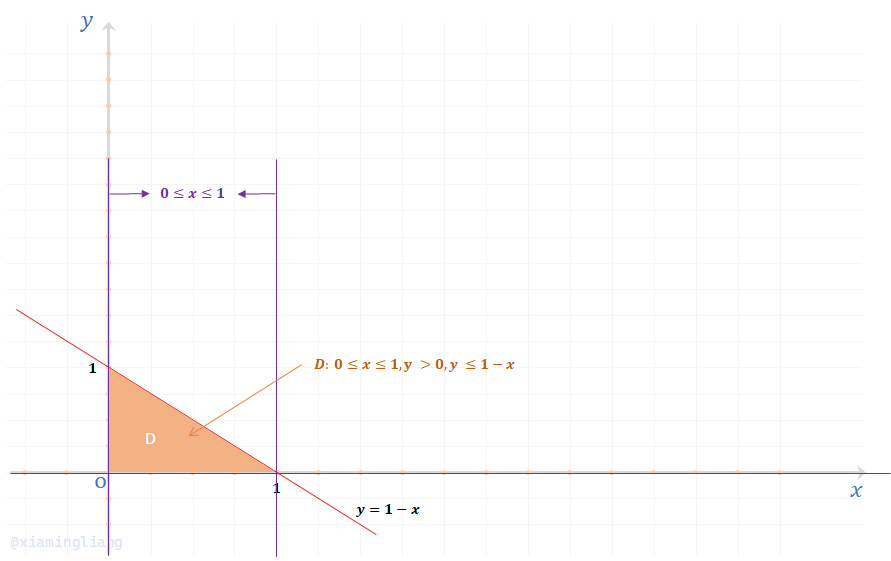
由此：

\[\begin{align} P\{X+Y \le 1\} &= \iint_{X+Y\le1} f(x,y) dxdy \\ &= \int_{0}^{1} (\int_{0}^{1-x} f(x,y)dy)dx \\ &= \int_{0}^{1} (\int_{0}^{1-x} \frac{1}{2} e^{-\frac{1}{2}y} dy)dx \\ &= \int_{0}^{1} (-e^{-\frac{1}{2}y} | _{0}^{1-x})dx \\ &= \int_{0}^{1} [-e^{-\frac{1}{2}(1-x)} -(-1)]dx \\ &= \int_{0}^{1} [1-e^{-\frac{1}{2}(1-x)} ]dx \ \ \ \ \ \ \ \ \ \ \ \#\ 提示：令u=e^{-\frac{1}{2}(1-x)},再使用复合函数求导的思路来解决 \\ &= (x-2e^{-\frac{1}{2}(1-x)}) |_0^1 \\ &= 2e^{-\frac{1}{2}} - 1 \end{align} \]

书上没有这么细致，我这里尽可能地详细化每一个等式变化。

（3）与（2）计算过程基本一致；图像如下：

\[\begin{align} P\{X+Y \le 1\} &= \iint_{X+Y\le 3} f(x,y) dxdy \\ &= \int_{0}^{1} (\int_{0}^{3-x} f(x,y)dy)dx \\ &= \int_{0}^{1} (-e^{-\frac{1}{2}y} | _{0}^{3-x})dx \\ &= \int_{0}^{1} [1-e^{-\frac{1}{2}(3-x)} ]dx \\ &= (x-2e^{-\frac{1}{2}(3-x)}) |_0^1 \\ &= 2e^{-\frac{3}{2}} - 2e^{-1} + 1 \end{align} \]

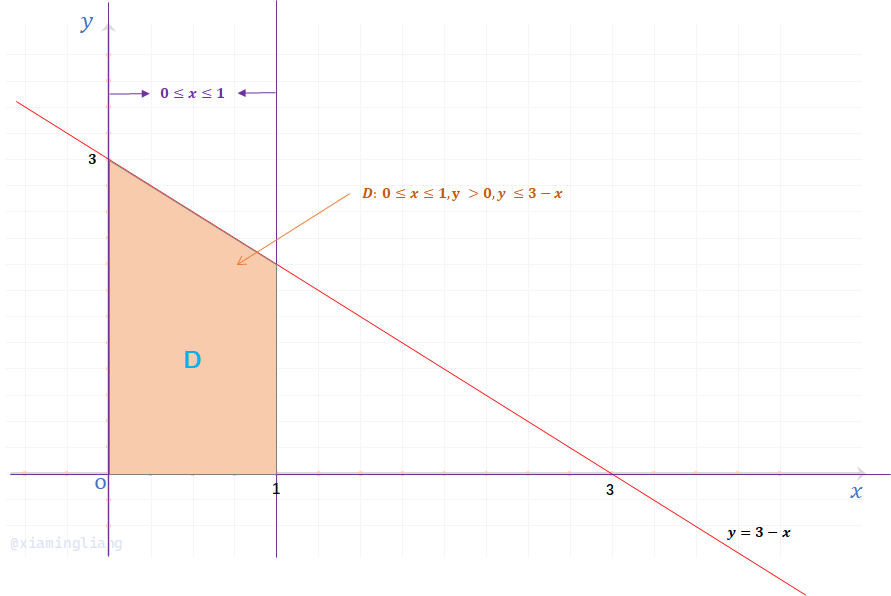
例5：设二维随机变量\((X,Y)\)的概率密度为\(f(x,y)\)，关于\(X,Y\)的边缘概率密度分别为\(f_X(x)\)和\(f_Y(y)\)，\(X\)与\(Y\)相互独立，求\(Z=X+Y\)的概率密度。

解：因为\(X\)与\(Y\)相互独立，则：\(f(x,y) = f_X(x) \cdot f_Y(y)\)；\(Z = X+Y\)的分布函数为：

\(F_Z(z) = P\{Z \le z\} = P\{X+Y \le z\} = \iint_{x+y \le z} f(x,y) dxdy \\\)

接下来画图（合理假定\(z\)是正数，实际上\(z\)是正是负与最终结果无关的）：

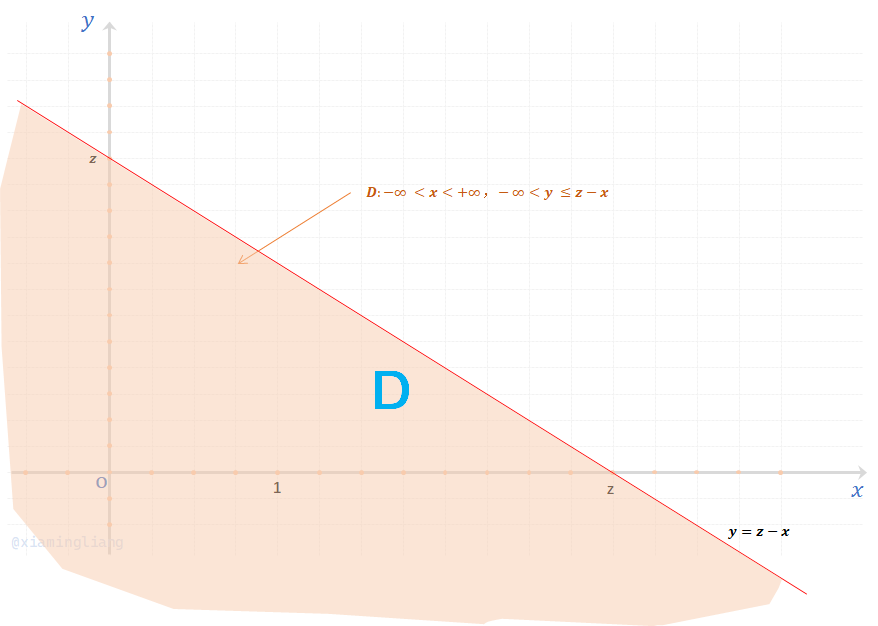
因此，上述等式可以转化为：

\[\begin{align} F_Z(z) = P\{Z \le z\} = P\{X+Y \le z\} &= \iint_{x+y \le z} f(x,y) dxdy \\ &= \int_{-\infty}^{+\infty} [ \int_{-\infty}^{+\infty} f(x,y) dy]dx \\ &= \int_{-\infty}^{+\infty} [ \int_{-\infty}^{z-x} f(x,y) dy]dx \\ &= \int_{-\infty}^{+\infty} [ \int_{-\infty}^{y的积分上限} f(x,y) dy]dx \\ &= \int_{-\infty}^{+\infty} [ \int_{-\infty}^{z-x} f(x,z-x) dy]dx \\ \end{align} \]

因此：\(f_Z(z) = {F_Z}'(z) = \int_{-\infty}^{+\infty} f(x,z-x) dx\)；

同理：\(f_Z(z) = {F_Z}'(z) = \int_{-\infty}^{+\infty} f(z-y,y) dy\)。

当\(X\)与\(Y\)相互独立时可以表示为：

$f_Z(z) = {F_Z}'(z) = \int_{-\infty}^{+\infty} f(x,z-x) dx = \int_{-\infty}^{+\infty} f_X(x) \cdot f_Y(z-x) dx $；

$f_Z(z) = {F_Z}'(z) = \int_{-\infty}^{+\infty} f(z-y,y) dy = \int_{-\infty}^{+\infty} f_X(z-y) \cdot f_Y(y) dy $。

这也被称作：独立随机变量和的卷积公式。

例6：设随机变量\(X\)与\(Y\)相互独立，都服从标准正态分布\(N(0,1)\)，求\(Z=X+Y\)的概率密度。

解：由题目知，\(X\)与\(Y\)的概率密度分别为：

\(f_X(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}},\ \ -\infty \lt x \lt +\infty;\ \ \ \ f_Y(y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}},\ \ -\infty \lt y \lt +\infty\)

又因\(X\)与\(Y\)相互独立，所以\((X,Y)\)的概率密度为：

\(f(x,y) = f_X(x) \cdot f_Y(y) = \frac{1}{2\pi} e^{-\frac{x^2+y^2}{2}},\ \ -\infty \lt x,y \lt +\infty\)

得\(Z=X+Y\)的概率为：

\[\begin{align} f_Z(z) = \int_{-\infty}^{+\infty} f_X(x) \cdot f_Y(z-x) dx &= \int_{-\infty}^{+\infty} \frac{1}{2\pi} e^{-\frac{x^2 +(z-x)^2}{2}} dx \\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} e^{-\frac{x^2 + z^2 - 2zx + x^2}{2}} dx \\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} e^{-\frac{2x^2 + z^2 - 2zx}{2}} dx\\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} e^{-\frac{2x^2 + \frac{z^2}{2} - 2zx + \frac{z^2}{2}}{2}} dx \\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} e^{-\frac{2(x^2-zx+\frac{z^2}{4}) + \frac{z^2}{2}}{2}} dx \\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} e^{-\frac{2(x^2-zx+\frac{z^2}{4})}{2}} \cdot e^{-\frac{z^2}{4}} dx \\ &= \frac{e^{-\frac{z^2}{4}}}{2\pi} \int_{-\infty}^{+\infty} e^{-(x^2-zx+\frac{z^2}{4})} dx \ \ \ \ \ \ \ \ \# 令u=x-\frac{z}{2},则u^2 = x^2-xz+\frac{z^2}{4},du=dx\\ &= \frac{e^{-\frac{z^2}{4}}}{2\pi} \int_{-\infty}^{+\infty} e^{-u^2} du \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \#u和x的取值范围没有变化 \end{align} \]

这里补充个重要的等式：\(\int_{-\infty}^{+\infty} e^{-x^2} dx = \sqrt{\pi}\)，所以：

\(f_Z(z) = \frac{1}{2\pi} \cdot e^{-\frac{z^2}{4}} \cdot \sqrt{\pi} = \frac{1}{2\sqrt{\pi}} \cdot e^{-\frac{z^2}{4}} = \frac{1}{\sqrt{2\pi} \sqrt{2}} \cdot e^{-\frac{(z-0)^2}{2(\sqrt{2})^2}}\)

即：\(Z \sim N(0,2)\)

\(\bigstar \bigstar \bigstar \bigstar \bigstar\)

一般地，\(X \sim N(\mu,\sigma_1^2),\ \ Y \sim N(\mu, \sigma_2^2)\)且\(X\)与\(Y\)相互独立，则\(Z = X+Y\)仍然服从正态分布，\(Z \sim N(\mu_1 + \mu_2,\ \sigma_1^2 + \sigma_2^2)\)；且可推广到\(n\)个或无限个独立正态分布的随机变量的情形，即：

当\(X_i \sim N(\mu_i,\ \sigma_i^2),\ \ i=1,2,...,n,...\)且它们之间是相互独立的则可知：\(X_1+X_2+...+X_n \sim N(\sum_{i=1}^{n} \mu_i,\ \sum_{i=1}^{n} \sigma_i^2)\)且更进一步证明任意有限个独立正态随机变量的线性组合仍服从正态分布，即：

若\(X_k \sim N(\mu_k,\ \sigma_k^2),\ \ k=1,2,...,n\)且它们之间是相互独立的则可知：\(a_1X_1+a_2X_2+...+a_nX_n \sim N(\sum_{i=1}^{n} a_i\mu_i,\ \sum_{i=1}^{n} (a_i\sigma_i)^2)\)，其中\(a_1,a_2,...,a_n\)为任意实数。

这里是很重要的结论！！

例7：设\(X \sim N(0,1),\ Y \sim N(1,1),\ Z \sim N(1,2)\)，随机变量\(X,Y,Z\)间相互独立，求\(3X+2Y+Z\)的分布。

解：由于随机变量\(X,Y,Z\)间相互独立且都服从中泰分布，则：

\(3X+2Y+Z \sim N(3\cp 0+2\cp 1+ 1\cp 1,\ (3\cp 1)^2+(2\cp 1)^2+(1\cp 2)^2) = N(3,\ 17)\)

教材上结果是\(N(3,15)\)明显是错误的。