传热学二维瞬态导热问题（编程作业）

注：本文仅供交流学习使用！

题目详情

---

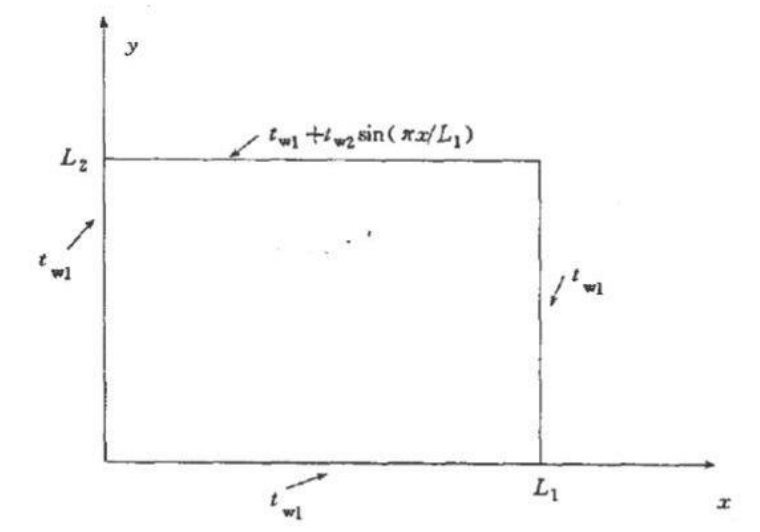
如图所示，⼀个⽆限⻓矩形柱体，其横截⾯的边⻓分别为 L₁ 和 L₂，常物性。该问题可视为⼆维稳态导热问题，边界条件如图中所示，其中 L₁ = 0.7 m，L₂ = 0.5 m，T_w1 = 80 ℃，T_w2 = 10 ℃，λ = 15 W/(m·K)。
(1) 编写程序求解⼆维导热⽅程。
(2) 绘制 x = L1/2 和 y = L2/2 处的温度场。

求解过程

---

1. 划分 L₁*L₂ 网格，步长为 1，定义初始温度场为 80.0 ℃
2. 根据题中边界条件定义边界温度
   ① 在 L₁、L₂ 接近时，定义四周边界温度
   ② 在 L₂ << L₁ 时，定义 y = 0 和 y = L₂ 处温度
3. 计算不包含边界的内部各点温度，每个点温度为它周围 8 个点温度的均值

$$ t_{m, n}=\frac{1}{8}\left(t_{m-1, n-1}+t_{m-1, n}+t_{m-1, n+1}+t_{m, n-1}+t_{m, n+1}+t_{m+1, n-1}+t_{m+1, n}+t_{m+1, n+1}\right) $$

4. 在 L₂ << L₁ 时，视为一维导热，内部各点温度为它上下两点温度均值

\[t_{m, n}=t_{m, n-1}+t_{m, n+1} \]

5. 判定连续两次计算得到的温度差值是否满足：

\[\max \left|t_{m, n}^{k+1}-t_{m, n}^{k}\right|<0.0000001 \]

6. 绘制热力图
7. 计算从 y = 0 处的导热量

\[\emptyset=\lambda \Delta y \frac{t_{m, 0}-t_{m, 1}}{\Delta x} \]

求解结果（部分）

---

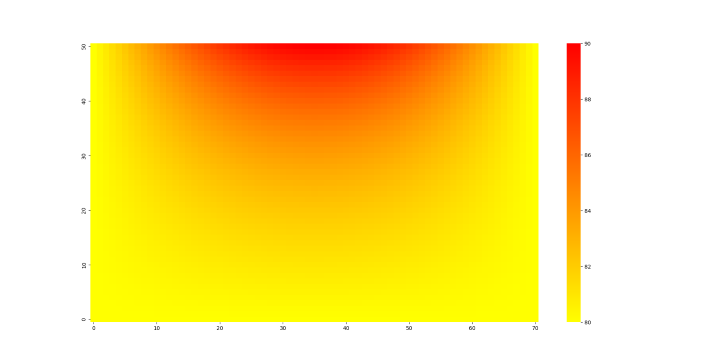
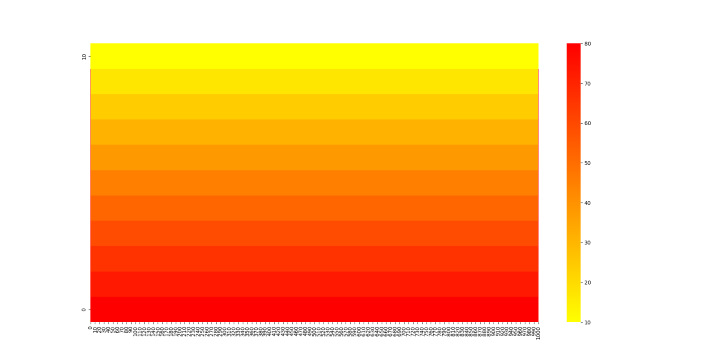
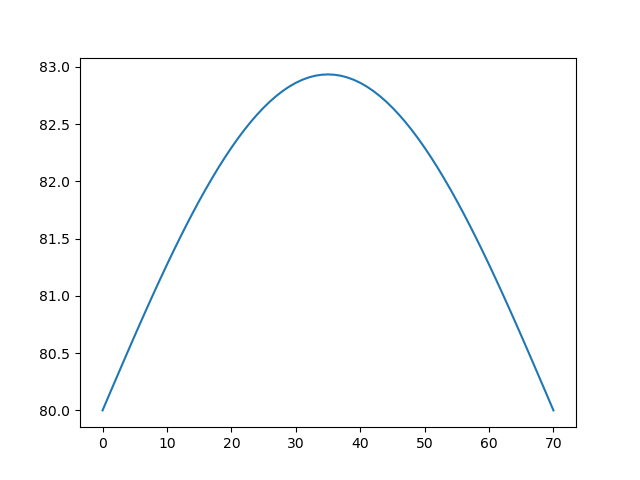
源码

---

from numpy import math,arange
import seaborn as sns
import matplotlib.pyplot as plt

def temp():
    """计算内部各点的温度"""
    nmnm = 0
    while True:
        for j in range(1,L2):
            for i in range(1,L1):
                T[j][i]=0.125*(T[j][i+1] + T[j+1][i] + T[j][i-1] + T[j-1][i] +  # 计算内部每个点的温度
                               T[j+1][i+1] + T[j+1][i-1] + T[j-1][i-1] + T[j-1][i+1])  # 内部每个点温度是周围8个点温度的均值
                juedui = abs(nmnm-float(T[j][i]))
        if juedui < 0.0000001:  # 判定两次计算的温度差值的绝对值
            break
        else:
            nmnm = T[j][i]

def picture():
    """绘制温度分布图"""
    fig = plt.figure()
    sns.heatmap(T, cmap=plt.cm.autumn_r, xticklabels=10, yticklabels=10).invert_yaxis()  # 反转坐标轴
    plt.show()

# 定义初始条件
λ = 15
L1 = 70
L2 = 50
Tw1 = 80.0
Tw2 = 10.0

# （1）绘制温度图，求解二维导热方程
T = [[80.000 for i in range(L1+1)] for j in range(L2+1)]  # 构建70*50的网格，定义初场温度为80
for i in range(0,L1+1):
    T[0][i] = Tw1  # y=0处温度
    T[L2][i] = float(Tw1 + Tw2 * math.sin(math.pi * i / L1))  # y=L2处温度
for i in range(0,L2+1):
    T[i][0] = Tw1
    T[i][L1] = Tw1  # x=0和x=L1处温度

temp()
picture()

# （2）绘制x=L1/2和y=L2/2处温度场
x = int(L1/2)
xx = []
y = int(L2/2)
yy = []

for i in range(L2+1):
    xx.append(T[i][x])
for j in range(L1+1):
    yy.append(T[y][j])

xxx = arange(0,len(xx),1)
yyy = arange(0,len(yy),1)
plt.plot(xxx,xx)
plt.show()
plt.plot(yyy,yy)
plt.show()

# （3）y=L2处t=Tw2，绘制二维温度图并计算y=0处传热量
Tw2 = 10.0

T = [[80.000 for i in range(L1+1)] for j in range(L2+1)]  # 构建70*50的网格，定义初场温度
for i in range(1,L1):
    T[0][i] = Tw1  # y=0处温度
    T[L2][i] = Tw2  # y=L2处温度
for i in range(1,L2):
    T[i][0] = Tw1
    T[i][L1] = Tw1  # x=0和x=L1处温度
T[L2][0] = 0.5*(T[L2-1][0]+T[L2][1])
T[L2][L1] = T[L2][0]
temp()
picture()

sum1 = 0  # 计算导热量他Φ2
for i in range(0, L1):
    quantity = λ * (T[0][i] - T[1][i])
    sum1 = sum1 + quantity
print('y=0处传导的热量为：' + str(sum1))

# (4)在L2<<L1时计算导热量
def heat_conduction(L1, L2):
    """计算L2<<L1时y=0处导热量，并求Φ2/Φ1"""
    T = [[80.000 for i in range(L1 + 1)] for j in range(L2 + 1)]
    for i in range(0, L1 + 1):
        T[0][i] = Tw1
        T[L2][i] = Tw2

    nmn = 0
    while True:
        for j in range(1, L2):
            for i in range(1, L1):
                T[j][i] = 0.5 * (T[j - 1][i] + T[j + 1][i])
                jueduizhi = abs(nmn - float(T[j][i]))
        if jueduizhi < 0.000001:
            break
        else:
            nmn = T[j][i]

    sum2 = 0  # 计算导热量Φ1
    for i in range(0, L1):
        quantity = λ * (T[0][i] - T[1][i])
        sum2 = sum2 + quantity
    print('L1=' + str(L1) + ' , L2=' + str(L2) + '时，y=0处传导的热量为：' + str(sum2)+
          ' ,Φ2/Φ1的值为: '+str(sum1/sum2))

    fig = plt.figure()
    sns.heatmap(T, cmap=plt.cm.autumn_r, xticklabels=10, yticklabels=10).invert_yaxis()  # 反转坐标轴
    plt.show()

# L2/L1=0.007、0.01、0.05、0.08、0.1时导热量
heat_conduction(1000,7)
heat_conduction(1000,10)
heat_conduction(1000,50)
heat_conduction(1000,80)
heat_conduction(1000,100)

本文作者：夏课

本文链接：https://www.cnblogs.com/xiakela/p/16961676.html

版权声明：原创文章，采用 CC BY-NC-ND 协议 进行许可

资源扩散：欢迎扩散💗转载请注明原文链接

联系博主：放一个 邮箱💌 在这