工程流体力学一维流动损失问题（编程作业）

注：本文仅供交流学习使用！

题目详情

---

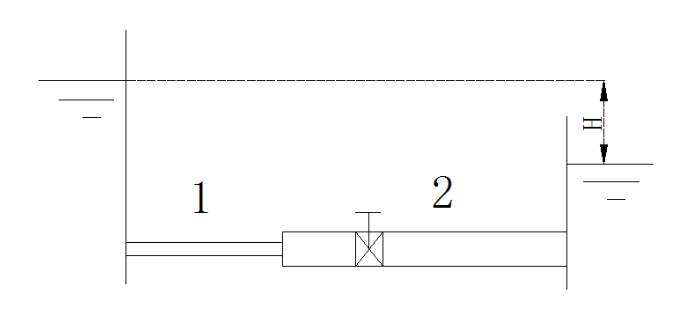
往车间容器送水的输水管道是由两段新的无缝不锈钢管串联而成，已知
d₁ = 20 cm ，
L₁ = 30 m ，
d₂ = 40 cm ，
L₂ = 60 m ，
管 1 为锐边进口，管 2 上的阀门的损失系数 \(\xi\) = 3.5 .
已知上游压力水塔具有的总水头是 12 m ，试求通过管道的体积流量。

计算分析

---

已知条件

管道 1 入口处    \(\xi_{1} = 0.5\)
两管道交界处    \(\xi_{2}=\left(1-\frac{d_{1}{ }^{2}}{d_{2}{ }^{2}}\right)^{2}=0.5625\)
阀门处       \(\xi_{3} = 3.5\)
管道 2 出口处    \(\xi_{4} = 1\)
20 ℃ 水的粘度    \(\nu = 1.007\times10^{-6}\) m²/s
绝对粗糙度     \(\varepsilon = 0.046\) mm

计算公式

$$ H=h_{f}+h_{j}=\left(\lambda \frac{l}{d}+\xi\right) \frac{v^{2}}{2 g}=\left(\lambda_{1} \frac{l_{1}}{d_{1}}+\xi_{1}+\xi_{2}\right) \frac{v_{1}{ }^{2}}{2 g}+\left(\lambda_{2} \frac{l_{2}}{d_{2}}+\xi_{3}+\xi_{4}\right) \frac{v_{2}{ }^{2}}{2 g} $$

$$ \lambda^{-1 / 2}=-2 \log \frac{\varepsilon}{3.71 d}+\frac{2.51}{\operatorname{Re} \lambda^{1 / 2}} $$ $$ \lambda=\left[\frac{2.51-R e}{2 R e \log \frac{\varepsilon}{3.71 d}}\right]^{2} $$ $$ R e=\frac{v d}{v} $$ $$ \frac{\pi}{4} d_{1}^{2} v_{1}=\frac{\pi}{4} d_{2}^{2} v_{2} $$

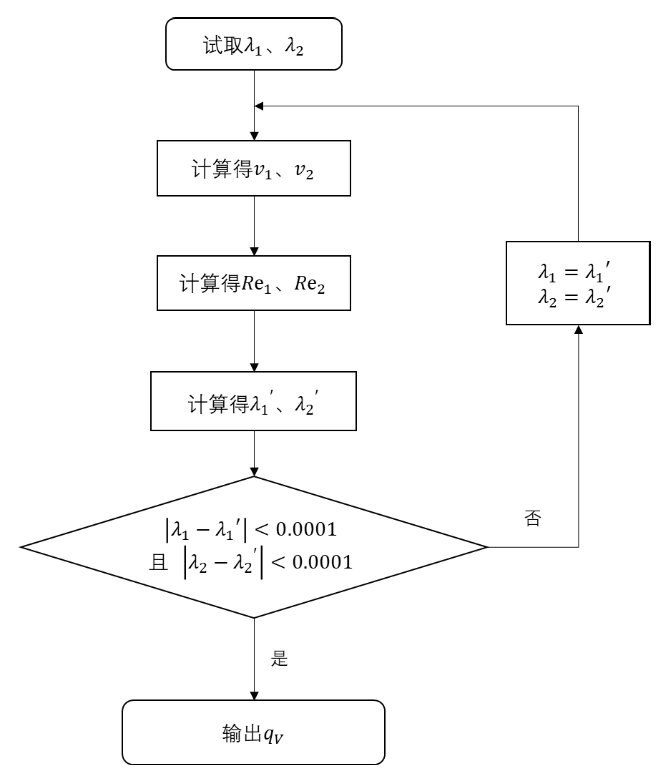
计算流程

试取 λ₁ 、λ₂ 并代入 H 中得到 v₁ 、v₂ ，由 v₁ 、v₂ 计算出对应的 λ₁ 、λ₂ ，并以此 λ₁ 、λ₂ 作为改进值，重复上述计算。当连续两次计算得到对应 λ 的差值小于 0.0001 ，可认为沿程损失系数符合要求。此时得到的 v₁ 、v₂ 正是符合要求的流速。
通过管道的体积流量 $$q_{v}=\frac{\pi}{4} d_{2}{ }^{2} v_{2}$$

程序框图

---

源码

---

import numpy as np
import math as mt   

def sunshi_yancheng(sd, zj):   # 定义函数求沿程损失系数
    """求沿程能量损失系数ss"""
    re = sd * zj / n
    c1 = (2.51-re)
    c2 = m/(3.71*zj)
    c3 = np.log10(c2)
    ss = (c1/(2*re*c3))**2  # 沿程损失系数
    return ss  # 将值存储在函数中

d1 = 0.2  # 管道1直径
d2 = 0.4  # 管道2直径
l1 = 30  # 管道1长度
l2 = 60  # 管道2长度
h = 12  # 损失水头
g = 9.8  # 重力加速度
a1 = 0.5  # 入口损失系数
a2 = (1-(d1**2)/d2**2)**2  # 管道1、2交界处损失系数
a3 = 3.5  # 阀门损失系数
a4 = 1  # 出口损失系数
n = 0.000001007  # 20摄氏度水的运动粘度
m = 0.000046  # 低碳钢管绝对粗糙度
ss1 = float(input("试取管道1沿程损失系数："))
ss2 = float(input("试取管道2沿程损失系数："))

while True:
    x = 16*(ss1*l1/d1+a1+a2)+ss2*l2/d2+a3+a4
    v = (2*g*h/x)**0.5  # 管道2内流速
    v1 = v*(d2**2)/(d1**2)  # 管道1内流速
    ss11 = sunshi_yancheng(v1, d1)
    ss22 = sunshi_yancheng(v, d2)  # 初始数据计算出的沿程损失系数
    pd1 = abs(ss11-ss1)
    pd2 = abs(ss22-ss2)
    if pd1 < 0.0001 and pd2 < 0.0001:  # 误差判定
        break
    else:
        ss1 = ss11
        ss2 = ss22  # 将得到的沿程损失系数作为改进值，代入重复计算

pi = mt.pi
qv = pi*(d2**2)*v/4  # 体积流量
answer = '体积流量是'+str(qv)+'立方米每秒'
print("管道1沿程损失系数为"+str(ss1))
print("管道2沿程损失系数为"+str(ss2))
print(answer)

点击运行后手动输入 λ₁、λ₂ （输入任意数值即可，最后算出来的结果都在误差范围内）

本文作者：夏课

本文链接：https://www.cnblogs.com/xiakela/p/16916850.html

版权声明：原创文章，采用 CC BY-NC-ND 协议 进行许可

资源扩散：欢迎扩散💗转载请注明原文链接

联系博主：放一个 邮箱💌 在这