动态规划
动态规划
动态规划问题的一般形式就是求最值。
比如说让你求最长递增子序列呀,最小编辑距离呀等等。
求解动态规划的核心问题是穷举。因为要求最值,肯定要把所有可行的答案穷举出来,然后在其中找最值呗。
动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。
重叠子问题、最优子结构、状态转移方程就是动态规划三要素。
在实际的算法问题中,写出状态转移方程是最困难的
明确「状态」 -> 定义 dp 数组/函数的含义 -> 明确「选择」-> 明确 base case。
重叠子问题
之所以在动态规划中才提到重叠子问题,原因在于,动态规划是由于当前规模的问题可由更小的若干独立子问题的结果计算出来,这样一来,几乎都会有很多重叠子问题,因为是一层一层依赖计算的。
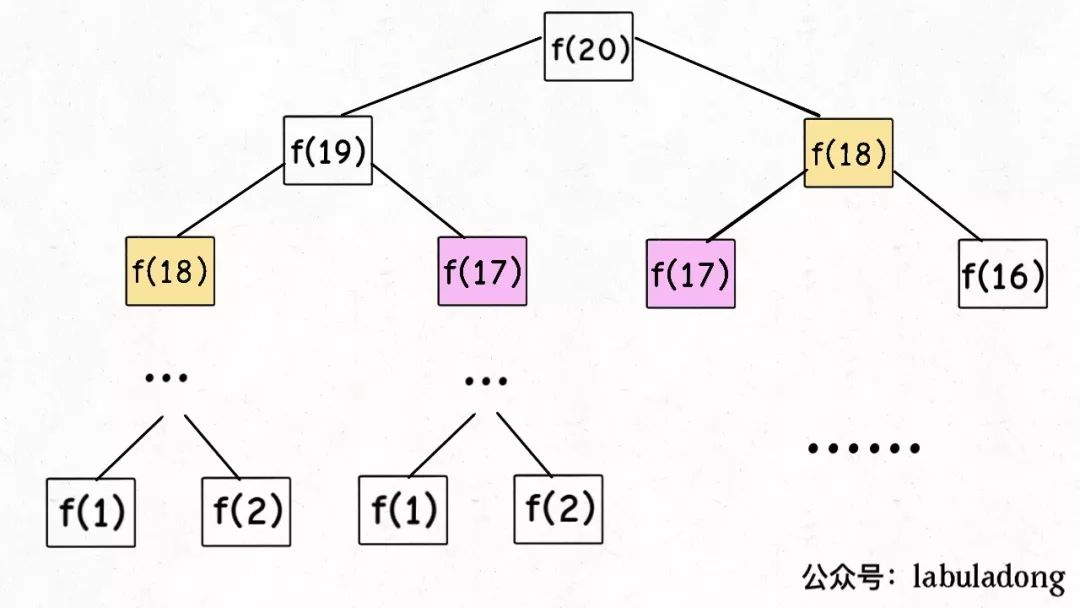
带「备忘录」的递归解法
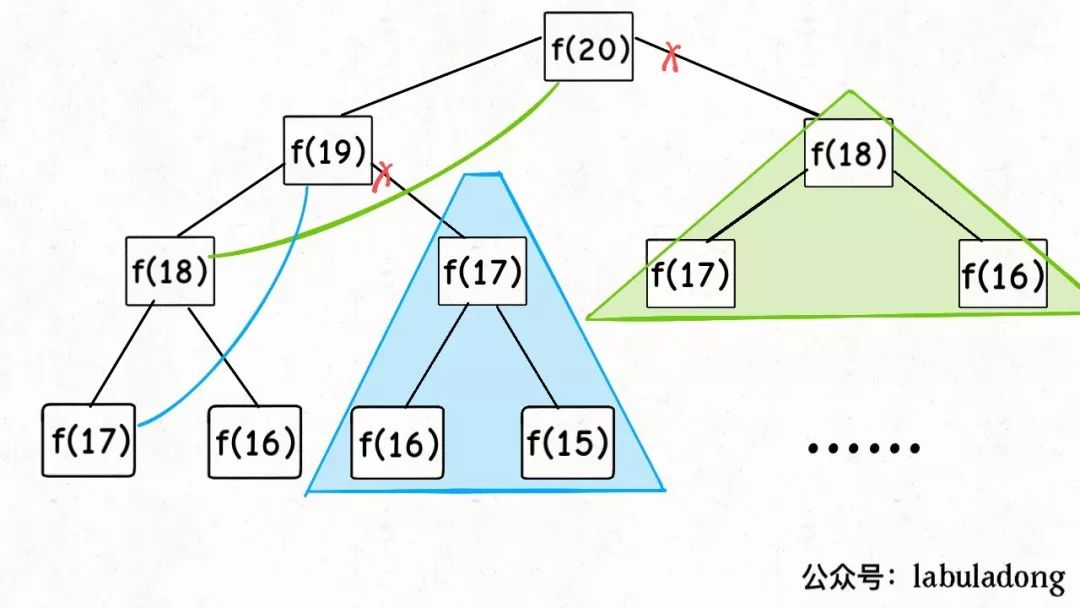
把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
如上图中,如果不用备忘录,会第二次进入f(17)这棵树(而且会遍历所有f(17)中的节点,这样节点数量将异常庞大)
使用备忘录后,时间复杂度降为 O(n)
dp 数组的迭代解法
两种解法其实是差不多的,大部分情况下,效率也基本相同。
状态转移方程
最优子结构
一、凑零钱问题
给你k种面值的硬币,面值分别为c1, c2 ... ck,每种硬币的数量无限,再给一个总金额amount,问你最少需要几枚硬币凑出这个金额,如果不可能凑出,算法返回 -1 。
// 凑零钱问题直接递归解法
function dpFn(coins, n) {
if (n == 0) { return 0; }
if (n < 0) { return -1; }
let res = Infinity; //求最小值,所以初始化为正无穷
coins.forEach(coin => {
let subRes = dpFn(coins, n - coin);
if (subRes == -1) { return; } // 子问题无解,跳过
res = Math.min(res, 1 + subRes);
});
res = res === Infinity ? -1 : res;
return res;
}
// 一共有三种 7元、9元、10元硬币,要凑出50元,返回最小硬币数量
dpFn([7, 9, 10], 50);
// 凑零钱问题带备忘录的递归解法
let cache = [];
function dpFn(coins, n) {
if (n == 0) { return 0; }
if (n < 0) { return -1; }
if (typeof cache[n] === 'number') { // 已经计算过了,直接使用结果
return cache[n];
}
let res = Infinity; //求最小值,所以初始化为正无穷
coins.forEach(coin => {
let subRes = dpFn(coins, n - coin);
if (subRes == -1) { return; } // 子问题无解,跳过
res = Math.min(res, 1 + subRes);
});
res = res === Infinity ? -1 : res;
cache[n] = res; // 缓存结果
return res;
}
// 一共有三种 7元、9元、10元硬币,要凑出50元,返回最小硬币数量
dpFn([7, 9, 10], 50);
// 凑零钱问题的dp数组迭代解法
function dpFn(coins, n) {
let dp = [0]; // dp 数组, 记录不同状态下的问题的解
// 注意,下面的遍历中已经排除了基本情况(i从1开始)
for (let i = 1; i <= n; i++) {
let res = Infinity; //求最小值,所以初始化为正无穷
coins.forEach(coin => {
if (i - coin < 0) { return; } // 必然无解,跳过
let subRes = dp[i - coin];
if (subRes == -1) { return; } // 子问题无解,跳过
res = Math.min(res, 1 + subRes);
});
res = res === Infinity ? -1 : res;
dp[i] = res;
}
return dp[n];
}
// 一共有三种 7元、9元、10元硬币,要凑出50元,返回最小硬币数量
dpFn([7, 9, 10], 50);
------------恢复内容开始------------
动态规划
动态规划问题的一般形式就是求最值。
比如说让你求最长递增子序列呀,最小编辑距离呀等等。
求解动态规划的核心问题是穷举。因为要求最值,肯定要把所有可行的答案穷举出来,然后在其中找最值呗。
动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。
重叠子问题、最优子结构、状态转移方程就是动态规划三要素。
在实际的算法问题中,写出状态转移方程是最困难的
明确「状态」 -> 定义 dp 数组/函数的含义 -> 明确「选择」-> 明确 base case。
重叠子问题
之所以在动态规划中才提到重叠子问题,原因在于,动态规划是由于当前规模的问题可由更小的若干独立子问题的结果计算出来,这样一来,几乎都会有很多重叠子问题,因为是一层一层依赖计算的。


带「备忘录」的递归解法
把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
如上图中,如果不用备忘录,会第二次进入f(17)这棵树(而且会遍历所有f(17)中的节点,这样节点数量将异常庞大)
使用备忘录后,时间复杂度降为 O(n)
dp 数组的迭代解法
两种解法其实是差不多的,大部分情况下,效率也基本相同。
状态转移方程
最优子结构
一、凑零钱问题
给你k种面值的硬币,面值分别为c1, c2 ... ck,每种硬币的数量无限,再给一个总金额amount,问你最少需要几枚硬币凑出这个金额,如果不可能凑出,算法返回 -1 。
// 凑零钱问题直接递归解法
function dpFn(coins, n) {
if (n == 0) { return 0; }
if (n < 0) { return -1; }
let res = Infinity; //求最小值,所以初始化为正无穷
coins.forEach(coin => {
let subRes = dpFn(coins, n - coin);
if (subRes == -1) { return; } // 子问题无解,跳过
res = Math.min(res, 1 + subRes);
});
res = res === Infinity ? -1 : res;
return res;
}
// 一共有三种 7元、9元、10元硬币,要凑出50元,返回最小硬币数量
dpFn([7, 9, 10], 50);
// 凑零钱问题带备忘录的递归解法
let cache = [];
function dpFn(coins, n) {
if (n == 0) { return 0; }
if (n < 0) { return -1; }
if (typeof cache[n] === 'number') { // 已经计算过了,直接使用结果
return cache[n];
}
let res = Infinity; //求最小值,所以初始化为正无穷
coins.forEach(coin => {
let subRes = dpFn(coins, n - coin);
if (subRes == -1) { return; } // 子问题无解,跳过
res = Math.min(res, 1 + subRes);
});
res = res === Infinity ? -1 : res;
cache[n] = res; // 缓存结果
return res;
}
// 一共有三种 7元、9元、10元硬币,要凑出50元,返回最小硬币数量
dpFn([7, 9, 10], 50);
// 凑零钱问题的dp数组迭代解法
function dpFn(coins, n) {
let dp = [0]; // dp 数组, 记录不同状态下的问题的解
// 注意,下面的遍历中已经排除了基本情况(i从1开始)
for (let i = 1; i <= n; i++) {
let res = Infinity; //求最小值,所以初始化为正无穷
coins.forEach(coin => {
if (i - coin < 0) { return; } // 必然无解,跳过
let subRes = dp[i - coin];
if (subRes == -1) { return; } // 子问题无解,跳过
res = Math.min(res, 1 + subRes);
});
res = res === Infinity ? -1 : res;
dp[i] = res;
}
return dp[n];
}
// 一共有三种 7元、9元、10元硬币,要凑出50元,返回最小硬币数量
dpFn([7, 9, 10], 50);


 浙公网安备 33010602011771号
浙公网安备 33010602011771号