排列组合子集
无论是排列、组合还是子集问题,简单说无非就是让你从序列 nums 中以给定规则取若干元素,主要有以下几种变体:
形式一、元素无重不可复选,即 nums 中的元素都是唯一的,每个元素最多只能被使用一次,这也是最基本的形式。
以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该只有 [7]。
形式二、元素可重不可复选,即 nums 中的元素可以存在重复,每个元素最多只能被使用一次。
以组合为例,如果输入 nums = [2,5,2,1,2],和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
形式三、元素无重可复选,即 nums 中的元素都是唯一的,每个元素可以被使用若干次。
以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该有两种 [2,2,3] 和 [7]。
形式四、元素可重可复选。
但既然元素可复选,那又何必存在重复元素呢?元素去重之后就等同于形式三,所以这种情况不用考虑。
重复 复选
× ×
√ ×
× √
√ √ 等价于 × √
上面用组合问题举的例子,但排列、组合、子集问题都可以有这三种基本形式,所以共有 9 种变化。
由于算出组合的同时,也就算出了子集,所以,本质上只有6种变化。
子集(元素无重不可复选)
[a,b,c] 的全部子集为 [] [a] [b] [c] [a,b] [a,c] [b,c] [a,b,c]
let res = [];
// 记录回溯算法的递归路径
let track = [];
// 回溯算法核心函数,遍历子集问题的回溯树
function backtrack( nums, start) {
// 前序位置,每个节点的值都是一个子集
res.push([...track]);
// 回溯算法标准框架
for (let i = start; i < nums.length; i++) {
// 做选择
track.push(nums[i]);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums, i + 1);
// 撤销选择
track.pop();
}
}
backtrack(['a', 'b', 'c'], 0);
console.log(res);
组合(元素无重不可复选)
[a,b,c] 的2元素的所有组合为 [a,b] [a,c] [bc]
let res = []; // 所有组合的结果
let track = []; // 记录回溯算法的递归路径
let max = 2; // 组合的个数
// 回溯算法核心函数,遍历子集问题的回溯树
function backtrack( nums, start) {
// 前序位置,每个节点的值都是一个子集
if(max === track.length){
res.push([...track]);
return;
}
// 回溯算法标准框架
for (let i = start; i < nums.length; i++) {
// 做选择
track.push(nums[i]);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums, i + 1);
// 撤销选择
track.pop();
}
}
backtrack(['a', 'b', 'c'], 0);
console.log(res);
排列(元素无重不可复选)
标准全排列可以抽象成如下这棵二完全叉树:
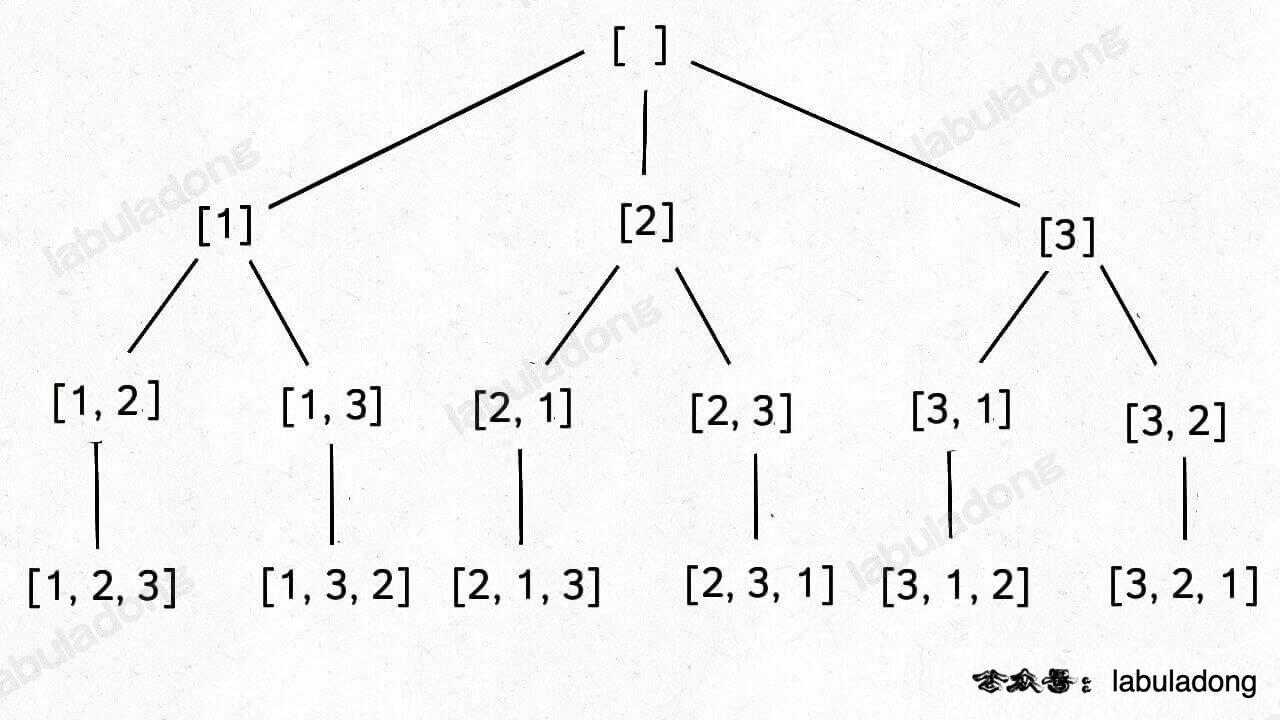
[a,b,c] 的2元素的所有排列为 [a,b] [a,c] [b,a] [b,c] [c,a] [c,b]
let res = []; // 所有排列的结果
let track = []; // 记录回溯算法的递归路径
let max = 2; // 排列的个数
let used = []; // 记录已经使用了的序号,防止重复
// 回溯算法核心函数,遍历子集问题的回溯树
function backtrack(nums) {
// 前序位置,每个节点的值都是一个子集
if (max === track.length) {
res.push([...track]);
return;
}
// 回溯算法标准框架
for (let i = 0; i < nums.length; i++) {
if (used[i]) { // 已经存在 track 中的元素,不能重复选择
continue;
}
// 做选择
track.push(nums[i]);
used[i] = true;
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums);
// 撤销选择
track.pop();
used[i] = false;
}
}
backtrack(['a', 'b', 'c']);
console.log(res);
子集/组合(元素可重不可复选)
[a,b,b] 的全部子集为 [] [a] [b] [a,b] [b,b] [a,b,b]
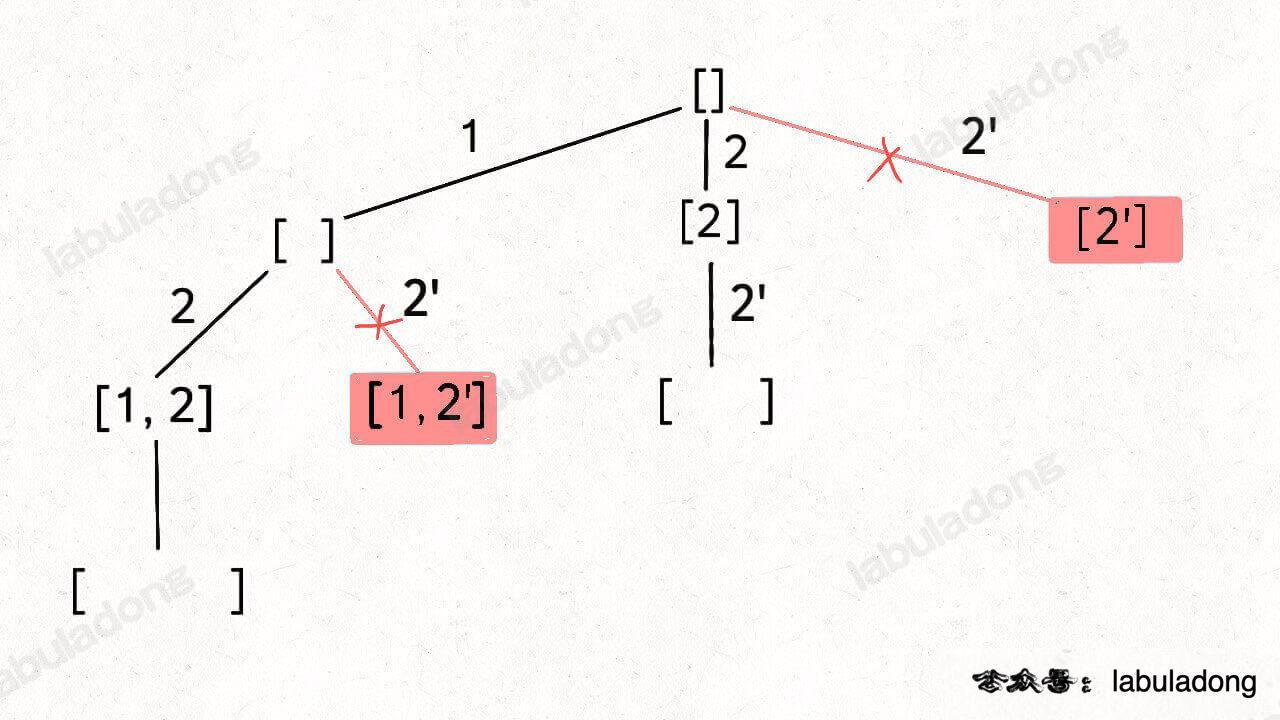
[a,b,b]需要先进行排序,让相同的元素靠在一起,如果发现 nums[i] == nums[i-1],则跳过
let res = []; // 所有组合的结果
let track = []; // 记录回溯算法的递归路径
// 回溯算法核心函数,遍历子集问题的回溯树
function backtrack( nums, start) {
// 前序位置,每个节点的值都是一个子集
res.push([...track]);
// 回溯算法标准框架
for (let i = start; i < nums.length; i++) {
// 剪枝逻辑,值相同的相邻树枝,只遍历第一条
if (i > start && nums[i] == nums[i - 1]) {
continue;
}
// 做选择
track.push(nums[i]);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums, i + 1);
// 撤销选择
track.pop();
}
}
let arr = ['a', 'b', 'b'];
arr.sort(); // 排序,将相同元素放在一起
backtrack(arr, 0);
console.log(res);
排列(元素可重不可复选)
[a,b,b] 的3元素的所有排列为 [a,b,b] [b,a,b] [b,b,a]
let res = []; // 所有排列的结果
let track = []; // 记录回溯算法的递归路径
let max = 3; // 排列的个数
let used = []; // 记录已经使用了的序号,防止重复
// 回溯算法核心函数,遍历子集问题的回溯树
function backtrack(nums) {
// 前序位置,每个节点的值都是一个子集
if (max === track.length) {
res.push([...track]);
return;
}
// 回溯算法标准框架
let prevNum = -666666; // 一个不可能出现在nums中的值
for (let i = 0; i < nums.length; i++) {
if (used[i]) { // 已经存在 track 中的元素,不能重复选择
continue;
}
// 新添加的剪枝逻辑,固定相同的元素在排列中的相对位置
if ( nums[i] === prevNum) {
continue;
}
// 做选择
track.push(nums[i]);
used[i] = true;
prevNum = nums[i];
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums);
// 撤销选择
track.pop();
used[i] = false;
}
}
let arr = ['a', 'b', 'b'];
arr.sort(); // 排序,将相同元素放在一起
backtrack(arr);
console.log(res);
子集/组合(元素无重可复选)
[a,b]的所有小于等于3的可复选子集为: [] [a] [a, a] [a,b] [a,c] [b] [b,b] [b,c] [c] [c,c]
跟 【子集/组合(元素无重不可复选)】只相差了一个地方,就是 backtrack(nums, i)
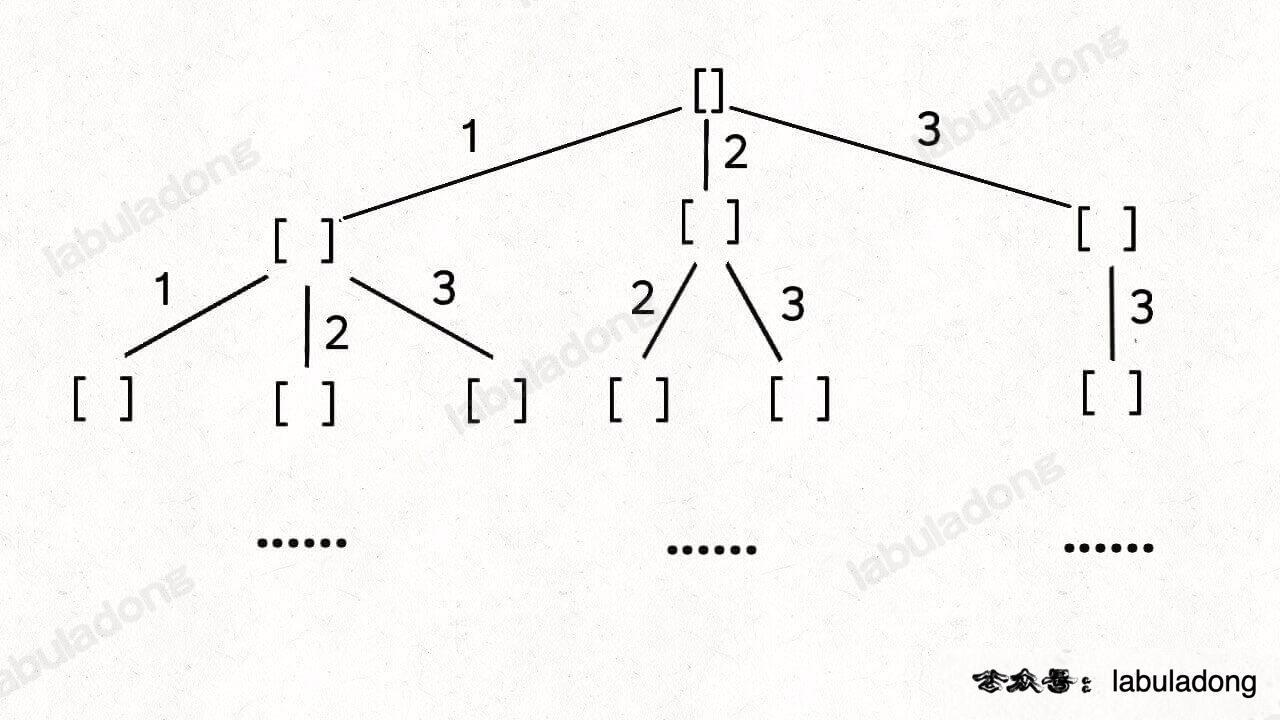
let res = [];
// 记录回溯算法的递归路径
let track = [];
let max = 2; // 最大数量
// 回溯算法核心函数,遍历子集问题的回溯树
function backtrack( nums, start) {
// 前序位置,每个节点的值都是一个子集
res.push([...track]);
if(track.length >= 2){
return;
}
// 回溯算法标准框架
for (let i = start; i < nums.length; i++) {
// 做选择
track.push(nums[i]);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums, i); // 注意,这里的i不加1,表示下一层使用的序号>=i,但是同一层上从左到右还是递增
// 撤销选择
track.pop();
}
}
backtrack(['a', 'b', 'c'], 0);
console.log(res);
排列(元素无重可复选)
[a,b,c]的2元素可复选的所有排列为:[a,a] [a,b] [a,c] [b,a] [b, b] [b,c] [c,a] [c,b] [c, c]
与 【排列(元素无重不可复选)】相比,只是简单的去掉去重的代码used数组即可。
let res = []; // 所有排列的结果
let track = []; // 记录回溯算法的递归路径
let max = 2; // 排列的个数
// 回溯算法核心函数,遍历子集问题的回溯树
function backtrack(nums) {
// 前序位置,每个节点的值都是一个子集
if (max === track.length) {
res.push([...track]);
return;
}
// 回溯算法标准框架
for (let i = 0; i < nums.length; i++) {
// 做选择
track.push(nums[i]);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums);
// 撤销选择
track.pop();
}
}
backtrack(['a', 'b', 'c']);
console.log(res);
不管是排列还是组合,在遍历的过程中都能取到问题规模更小的全部值
如 [a,b,c,d]的可重复不可复选排列(组合), 长度为3的所有结果,在生成结果的过程中,必然会生成 长度为2、长度为1、长度为0的所有结果。
所以,利用这一点,才能得到集合,算出组合的同时,也就算出了对应的集合。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号