二叉树

定义

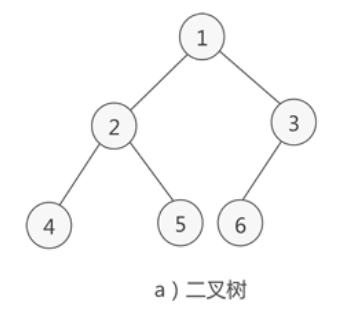
• 每一个节点的子节点数量小于等于2的树称为二叉树。
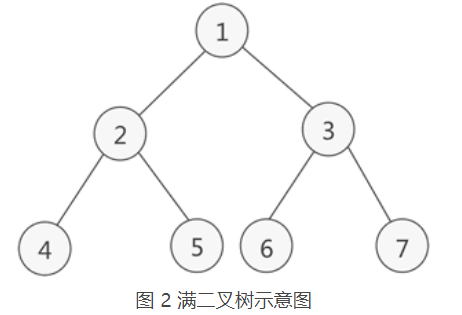
• 如果树中的每个节点的子节点数量均为2或0，且总数为2^n，则称为满二叉树。
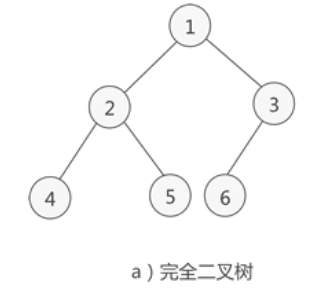
• 如果将有n个节点的满二叉树的所有节点从上到下，从左到右依次从0开始编号，$0,1,\ldots,i,\ldots,n-1$，去掉 节点i~n-1 后，这颗树就成为完全二叉树。完全二叉树除去最后一层节点后为满二叉树，且最后一层的结点依次从左到右分布。

 

最大深度：就是层数

表示

层数 n 和节点编号 i 均从0开始。节点编号从上到下，从左到右依次增加。

一颗二叉树使用一个一维数组来表示，节点的编号对应数组的下标，节点的值对应数组的值(对应下标处的)。如果节点不存在，则认为值是null。

如 arr = [8, 3, 2, 9, 7, null, 4] 表示 

第0层为 0号节点，其值为8   

第1层为 1号节点和2号节点，其值分别为3,2   

第2层为 3~6号节点，其值 分别为 9,7,空,4。

 

特性

1. 二叉树中，第 n 层最多有 $2^n$ 个结点。$(n \ge 0)$

2. 节点 i 位于第 n 层，则  $n = \lfloor log_{2}^{i+1}  \rfloor   \quad (n \ge 0,i \ge 0)$  即  n = Math.floor( Math.log2(i + 1) );  。      

3. 如果二叉树的层数为 n，那么此二叉树最多有 $2^{n+1} - 1$ 个结点。$(n \ge 0)$

4. 节点 i 的父节点编号为 $[\frac{i}{2}] - 1 \quad  (i \ge 1)$  即 Math.round(i/2) - 1; 。

5. 节点 i 的两个子节点的编号分别为 $i \times 2+1$ 和 $i \times 2 + 2$ 。$(i \ge 0)$

 

遍历

深度遍历

let arr = [8, 3, 2, 9, 7, null, 4]; // 二叉树
function dp(arr, i){ // 深度优先遍历
    if(i >= arr.length){
		return;
	}
	console.log('当前节的编号为:', i, ',值为:', arr[i], '位于第', Math.floor(Math.log2(i+1)) ,'层');
	dp(arr, i*2 + 1);
	dp(arr, i*2 + 2);
}
dp(arr, 0);

 

function dp(arr, i){ // 深度优先遍历, 模拟递归调用
	let stack = [i];
    while(stack.length > 0){
        i = stack.pop();
        if(i >= arr.length){
            continue;
        }
        console.log('当前节的编号为:', i, ',值为:', arr[i], '位于第', Math.floor(Math.log2(i+1)) ,'层');
        stack.push(i*2 + 2);
        stack.push(i*2 + 1);
    }
}
dp([8, 3, 2, 9, 7, null, 4], 0);

　　

 

按层遍历

let arr = [8, 3, 2, 9, 7, null, 4]; // 二叉树
function bp(arr){ // 按层遍历
    for(let i=0; i<arr.length; i++){
		console.log('当前节的编号为:', i, ',值为:', arr[i], '位于第', Math.floor(Math.log2(i+1)) ,'层');
	}
}
bp(arr);

　　

 

二叉搜索树（BST）又称二叉查找树或二叉排序树。

中序位置主要用在 BST 场景中，你完全可以把 BST 的中序遍历认为是遍历有序数组。

二叉搜索树性质

设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点，那么y.key≤x.key。如果y是x右子树中的一个结点，那么y.key≥x.key。

在二叉搜索树中：

1、若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值。

2、若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值。

3、任意结点的左、右子树也分别为二叉搜索树。

 

https://labuladong.github.io/algo/1/4/

二叉树的「直径」长度，就是任意两个结点之间的路径长度。最长「直径」并不一定要穿过根结点，比如下面这棵二叉树：

它的最长直径是 3，即 [4,2,1,3] 或者 [5,2,1,3] 这两条「直径」的长度。

分析：初步一看，要算直径无从下手，怎么遍历好像都算不出来，所以必须先将直径怎么算弄明白。

当一个问题看得不清楚时，首先看最简单的情况，从中找出规律。

当只有一个根节点时，最长直径显然是0

当有两层(最多3个节点)时，最长直径显然是2，如果只有一个左子树(或仅有右子树)，则最长直径为1

当有三层(最多7个节点)时，仔细观察一下，容易得出最长直径是4

当有四层时。。。，最长直径为。。。

明显得出结论，跟左子树和右子树有关。

所以 每一条二叉树的「直径」长度，就是一个节点的左右子树的最大深度之和。