计量经济学笔记

2025-2-12 chapter13

横截面数据混合在一起，混合横截面数据；
面板数据。两者的区别：前者两个截面独立，后者个体是一样的，但是时间不同。

两期面板数据(TWO-PERIOD PANEL DATA ANALYSIS)

横截面数据\(y_i = x_i\beta + v_i\)
面板数据\(y_{it} = x_{it}\beta + v_{it}\)有时间t
\(v_{it}= u_{it} + a_i\)
\(u_{it}\)是时间效应,随时间变化，\(a_i\)是固定效应，不随时间变化。这两者都是不可观测的，看不到的。
UEM模型：FE RE
固定效应模型：\(a_i与x_i相关,cov(a_i,x_i)!=0\)
随机效应模型：\(a_i与x_i无关\)

FE:固定模型

1、pols(ols，适用误差项与解释变量无关)：\(x_{it},v_{it}\)是否相关,相关，故ols方法不能用(a,x相关)。

\[y_{it} = x_{it} \beta + a_i + u_{it} \quad t=1,2 \]

\[t=2: \quad y_{i2} = x_{i2} \beta + a_i + u_{i2} \quad (1) \]

\[t=1: \quad y_{i1} = x_{i1} \beta + a_i + u_{i1} \quad (2) \]

两式相减可以消去\(a_i\),是为差分：

\[y_{i2} - y_{i1} = x_{i2}\beta - x_{i1}\beta + u_{i2}-u_{i1} \]

即差分形式：

\[\Delta y_{i2} = \Delta x_{i2} \beta + \Delta u_{i2} \quad (3) \]

\[\Delta y \equiv y_{2} - y_{1} \quad \Delta x \equiv x_{2} - x_{1} \]

此时，\(\Delta y\)与\(\Delta x\)不相关，可以用OLS估计。条件是\(\Delta x_{i2}, \Delta u_{i2}\)不相关。

从 (1) - (2) 得：

\[{y_{it} - \bar{y}_i} = (x_{it} - \bar{x}_i)\beta + u_{it} - \bar{u}_i \]

\[\ddot{y}_{it} = \ddot{x}_{it}\beta + \ddot{u}_{it} \quad (4) \]

对 (\ddot{y}{it}) 和 (\ddot{x}) 回归得到 (\hat{\beta}_{FE})
固定效应转变或者组内转变

\[\text{cov}(X_{i2} - X_{i1}, u_{i2} - u_{i1}) \]

\[= \text{cov}(X_{i2}, u_{i2}) - \text{cov}(X_{i2}, u_{i1}) - \text{cov}(X_{i1}, u_{i2}) + \text{cov}(X_{i1}, u_{i1}) \]

假设：称为严格外生假设

\[E(u_{it} \mid a_i, X_i) = 0, \quad X_i = (x_{i1}, x_{i2}) \]

假设含义：
1、\(Eu_{it}=0\)
2、\(cov(u_{it},a_i)=0\)
3、\(cov(u_{it},x_i)=0\)
这个假设无法保证\(x_i,a_i\)无关，所以FE模型假设\(x_i,a_i\)相关。

差分的代价：1.两期面板数据，损失一期信息，样本容量变少；2.差分后波动变小，估计量方差变大。可能导致原来显著的变为不显著。

证明题：

\[\text{Cov}(v_{i1}, v_{i2}) = \text{Var}(a_i) \]

证明如下：

\[\text{Cov}(V_{i1}, V_{i2}) = \text{Cov}(\hat{a}_i + u_{i1}, \hat{a}_i + u_{i2}) \]

\[= \text{Cov}(\hat{a}_i, \hat{a}_i) + \text{Cov}(\hat{a}_i, u_{i2}) + \text{Cov}(u_{i1}, \hat{a}_i) + \text{Cov}(u_{i1}, u_{i2})\\ = \text{Var}(a_i)\]

\(\beta\)写在x后面，x有多个

第十四章

自由度问题

2025-5-19

组内估计与组间估计区别与联系

自由度为什么是N(T-1)-K?

\[\ddot{y}_{it} = \ddot{x}_{it} \beta + \ddot{u}_{it} \quad (3) \]

\[\ddot{y}_{it} = y_{it} - \bar{y}_i, \quad i = 1, \ldots, N \]

\[t = 1, \ldots, T \]

自由度推导：

\[NT - K - N \]

这里，NT 是总的观测值数量，K 是模型中参数的数量（包括截距），N 是个体的数量。自由度是从总观测值中减去模型参数的数量和个体数量得到的。

面板数据通常加入时间虚拟变量，是为了控制一些宏观（经济发展形势，技术进步）的发展因素

stata中egen,gen的区别，右边涉及函数的用egen

数据实例

use "D:\kuake\浙财\notebook\大三\计量经济学\chapter14\panel data report\JTRAIN.DTA",clear

// 法一
order lscrap d88 d89 grant grant_1
egen ad88=mean( d88),by (fcode)
egen ad89=mean( d89),by (fcode)
sum ad88 ad89
egen agrant=mean(grant),by (fcode)
egen agrant_1=mean(grant_1),by (fcode)
egen alscrap=mean( lscrap),by (fcode)
gen fd88= d88- ad88
gen fd89= d89- ad89
gen fgrant= grant- agrant
gen fgrant_1 = grant_1 - agrant_1
gen flscrap= lscrap- alscrap
reg flscrap fd88 fd89 fgrant fgrant_1,nocons

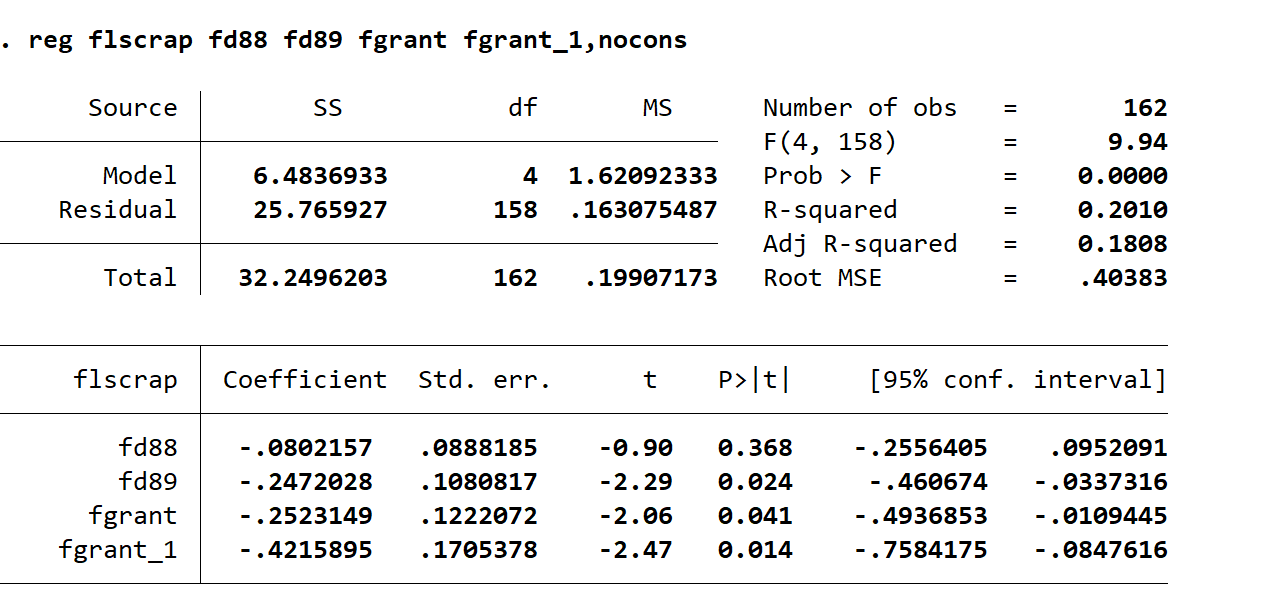
系数正确但是标准误错误
88年的废品率比87年低8%，89年比87年低24%。
企业得到支柱，对生产率有影响
标准误这时候不能用，因为自由度，应为这个自由度是依据162-4计算的。正确的标准误怎样计算？
NT-K-N
N=54,T=3,K=4,自由度=162-4-54=104.
fd88正确的标准误应怎么算？
一元线性回归模型：

\[y = \beta + \beta_1 x + u \]

估计系数 (\beta_1) 的方差：

\[\text{var}(\hat{\beta}_1) = \frac{\sigma^2}{\sum (x_i - \bar{x})^2}, \quad \hat{\sigma}^2 = \frac{\sum \hat{u}_i^2}{n-k} \]

n-k错误的是158，正确的104

\[\sqrt{\frac{\cdots}{104}} = \sqrt{\frac{\cdots}{158}} \times \sqrt{\frac{158}{104}} \]

计算表达式：
d88标准误

\[\text{di } 0.0888185 \times (158/104)^{0.5}\\ =0.10947569\]

正确标准误计算，一个好考点

法二；

iis fcode
tis year 
//[or tsset fcode year]
xtreg lscrap d88 d89 grant grant_1,fe

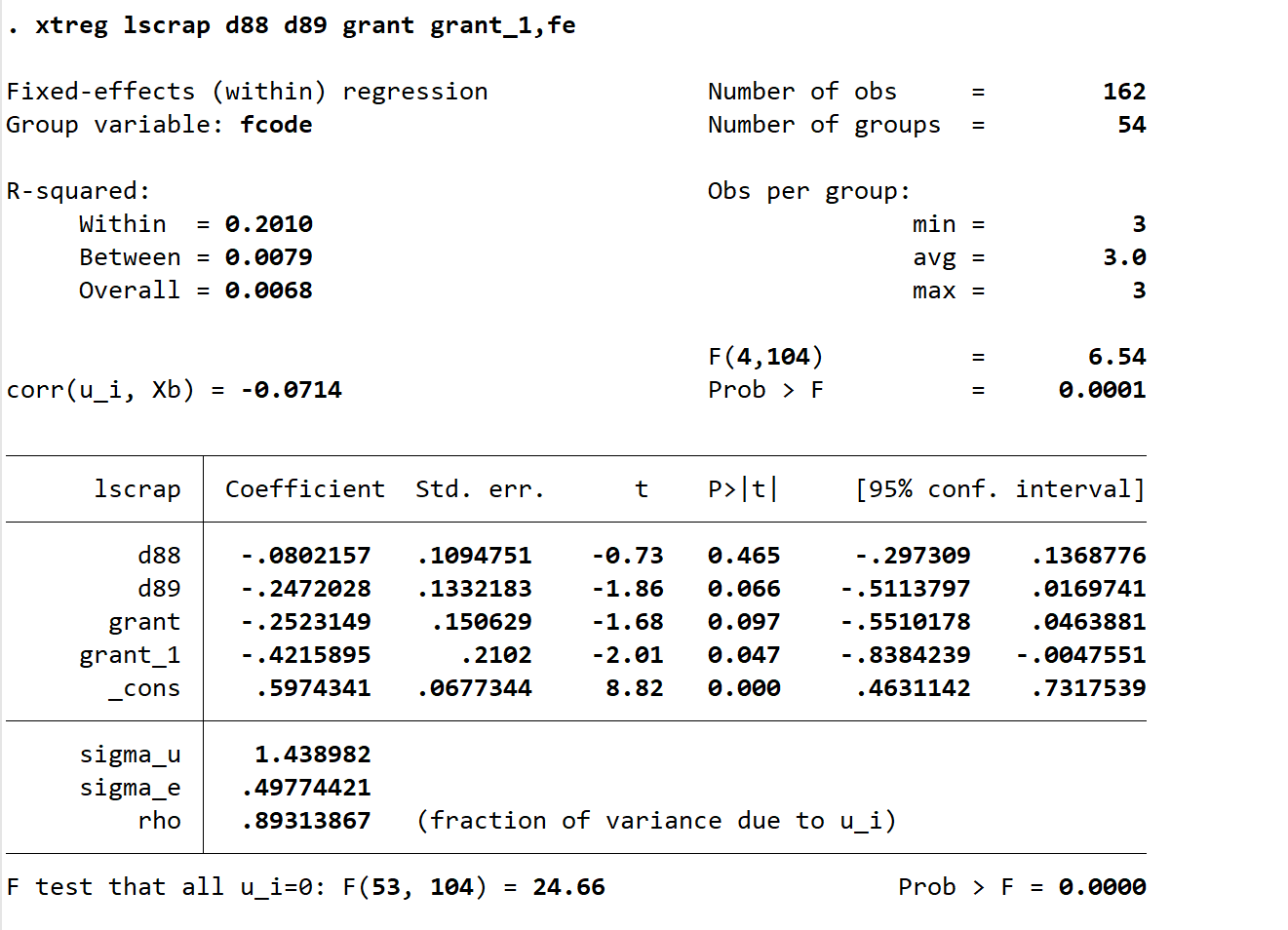
\(\beta\) 估计同上一样，标准误也正确，以后使用用这个即可。
within:表示组内估计
162=54*3
每个板块年份一致：平衡面板数据
\(R^2\) 有三个：应该用哪个？固定效益选那个？选组内估计的那个（Within）

F（4，104）统计量，拒绝原假设，这四个x对y有影响
通过相关系数判断fe还是RE?
这里的问题，为什么这里输出的结果有\(\beta_0\)?
54公司，有54个截距，

\[a_i,a_2....a_{54} \]

可以解释，给个平均，但一般不管它

\(\rho\) 是什么？方差，a的重要性，越接近1，越重要。
\(\rho=\frac{\sigma_u^2}{\sigma_u^2+\sigma_e^2}\)
模型中要不要放\(a_i\),在于它重要不重要。
计算表达式：

\[\frac{1.438982^2}{1.438982^2 + 0.49774421^2}\\ =0.89313866\]

这个F检验，原假设所有\(a_i=0\),
原假设应该这样表述：\(a_1=a_2=....a_{54}\)，实际上检验的是：在ols于FE之间怎么选择。拒绝原假设显著，说明应该用FE。接受原假设，应该用OLS。

数据实例二：教育的回报率有没有发生改变？

use "D:\kuake\浙财\notebook\大三\计量经济学\chapter14\panel data report\WAGEPAN.dta",clear

iis nr
tis year
gen edd81 = educ*d81
gen edd82 = educ*d82
gen edd83 = educ*d83
gen edd84 = educ*d84
gen edd85 = educ*d85
gen edd86 = educ*d86
gen edd87 = educ*d87
xtreg lwage expersq union married d81-d87 edd81-edd87, fe
test edd81 edd82 edd83 edd84 edd85 edd86 edd87

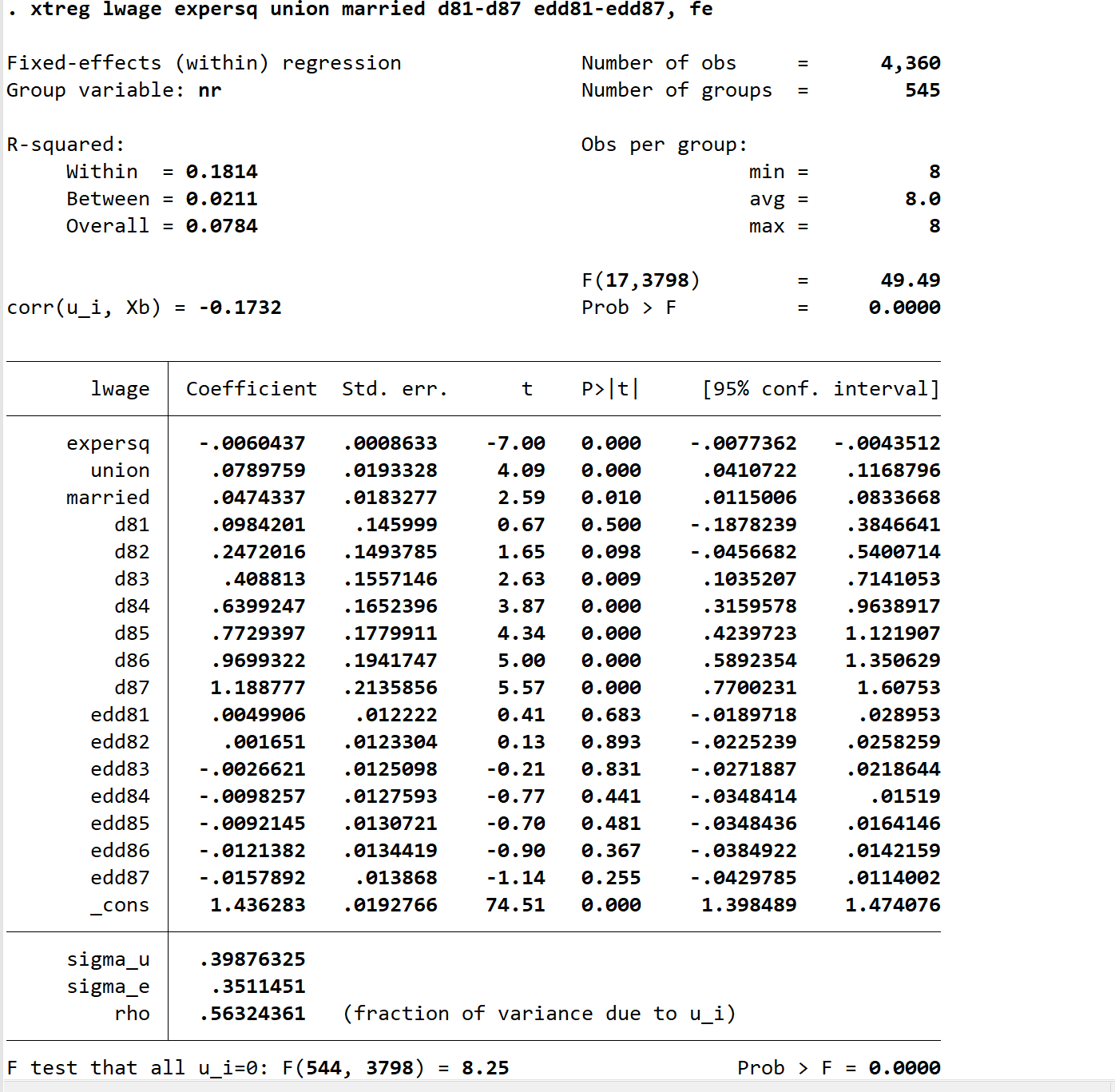
edd81,0.0049,81年教育系数与80年教育系数只差，多了0.0049，但是不显著；交互作用都不显著，初步判断，在这个期间，教育回报率没有发生改变。

2025-2-26

实验考试重点

7个范围，考6个
1、虚拟变量，系数解释，交互作用，尤其是两组不同的虚拟变量之间的比较，邹检验一定考。
2、ATE可能考，可能不考
3、工具变量，估计，内生性检验与过度识别检验（上机理论都要考）
4、logit,probit模型二选一，LR检验，APE注意（APE与PEA是不一样的），逆米尔斯系数,
5、tobit模型，一定考，算预测值，适不适合tobit；tobit模型的估计，系数的显著性；预测（注意：不看课件不知道）
6、possion必考：8小题，y的比例（>0,=0）;估计；\(\sigma^2\)的估计；标准误如何进行调整？
7、面板数据，FE，RE，\(\lambda\)怎么估计？

估计\(\lambda\)

FE与RE之间的共同点：\(u与x,u与a无关\)
a方差估计公式：

\[\hat{\sigma}_a^2 = \left[ \frac{NT(T-1)}{2} - (k+1) \right]^{-1} \sum_{i=1}^{N} \sum_{t=1}^{T-1} \sum_{s=t+1}^{T} \hat{v}_{it} \hat{v}_{is}, \]

协方差简便公式：
协方差公式：

\[\text{Cov}(X, Y) = E(XY) - E(X)E(Y) \]

方差计算：

\[\sigma_a^2 = E(v_{it} v_{is}) = \text{Cov}(v_{it}, v_{is}) \]

向量 ( \mathbf{v}_i ) 的定义：

\[\mathbf{v}_i = \begin{pmatrix} v_{i1} \\ \vdots \\ v_{iT} \end{pmatrix} \]

协方差矩阵
( \mathbf{Cov}(\mathbf{v}_i) ) 的定义：

\[ \mathbf{Cov}(\mathbf{v}_i) = \begin{pmatrix} \text{Var}(v_{i1}) & \text{Cov}(v_{i1}, v_{i2}) & \cdots & \text{Cov}(v_{i1}, v_{iT}) \\ \text{Cov}(v_{i2}, v_{i1}) & \text{Var}(v_{i2}) & \cdots & \text{Cov}(v_{i2}, v_{iT}) \\ \vdots & \vdots & \ddots & \vdots \\ \text{Cov}(v_{iT}, v_{i1}) & \text{Cov}(v_{iT}, v_{i2}) & \cdots & \text{Var}(v_{iT}) \end{pmatrix}_{T \times T} \]

主对角线上都是v的方差，其他地方都是a的方差
方差矩阵：

\[= \begin{pmatrix} \sigma_v^2 & \sigma_a^2 & \sigma_a^2 & \cdots & \sigma_a^2 \\ \sigma_a^2 & \sigma_v^2 & \sigma_a^2 & \cdots & \sigma_a^2 \\ \sigma_a^2 & \sigma_a^2 & \sigma_v^2 & \cdots & \sigma_a^2 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \sigma_a^2 & \sigma_a^2 & \sigma_a^2 & \cdots & \sigma_v^2 \end{pmatrix}_{T \times T} \]

对于 ( t = 1 )：

\[\frac{T}{2} \sum_{s=2}^{T} E(v_{i1} v_{is}) \]

对于 ( t = 2 )：

\[\frac{T}{2} \sum_{s=3}^{T} E(v_{i2} v_{is}) \]

...
对于 ( t = T-1 )：

\[\frac{T}{2} \sum_{s=T}^{T} E(v_{i, T-1} v_{i, T}) \]

\[\frac{T^2 - T}{2} \sigma_a^2 = E \left( \sum_{t=1}^{T-1} \sum_{s=t+1}^{T} v_{it} v_{is} \right) \]

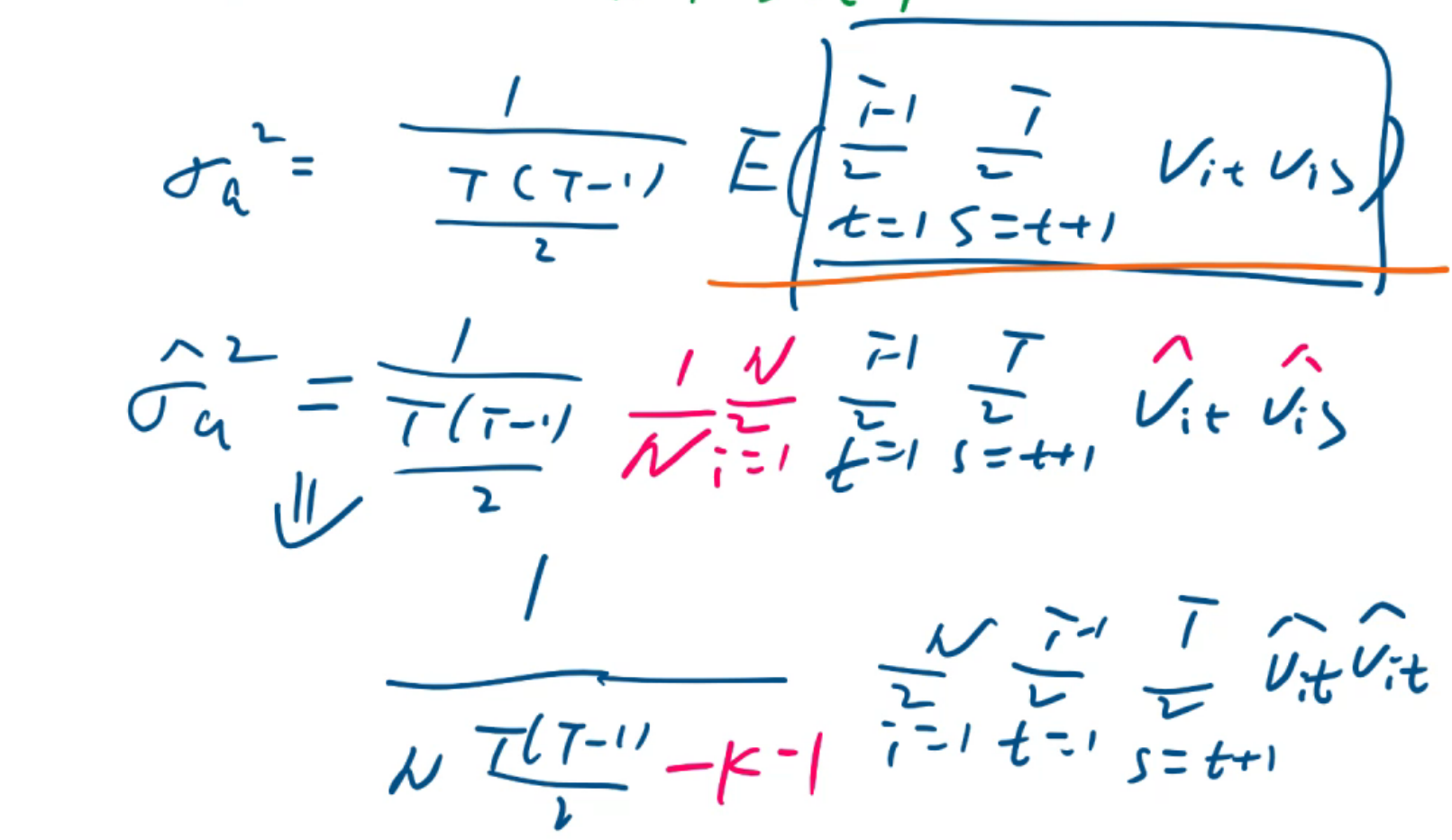
实验

use "D:\kuake\浙财\notebook\大三\计量经济学\chapter14\panel data report\WAGEPAN.dta",clear

des
iis nr
tis year
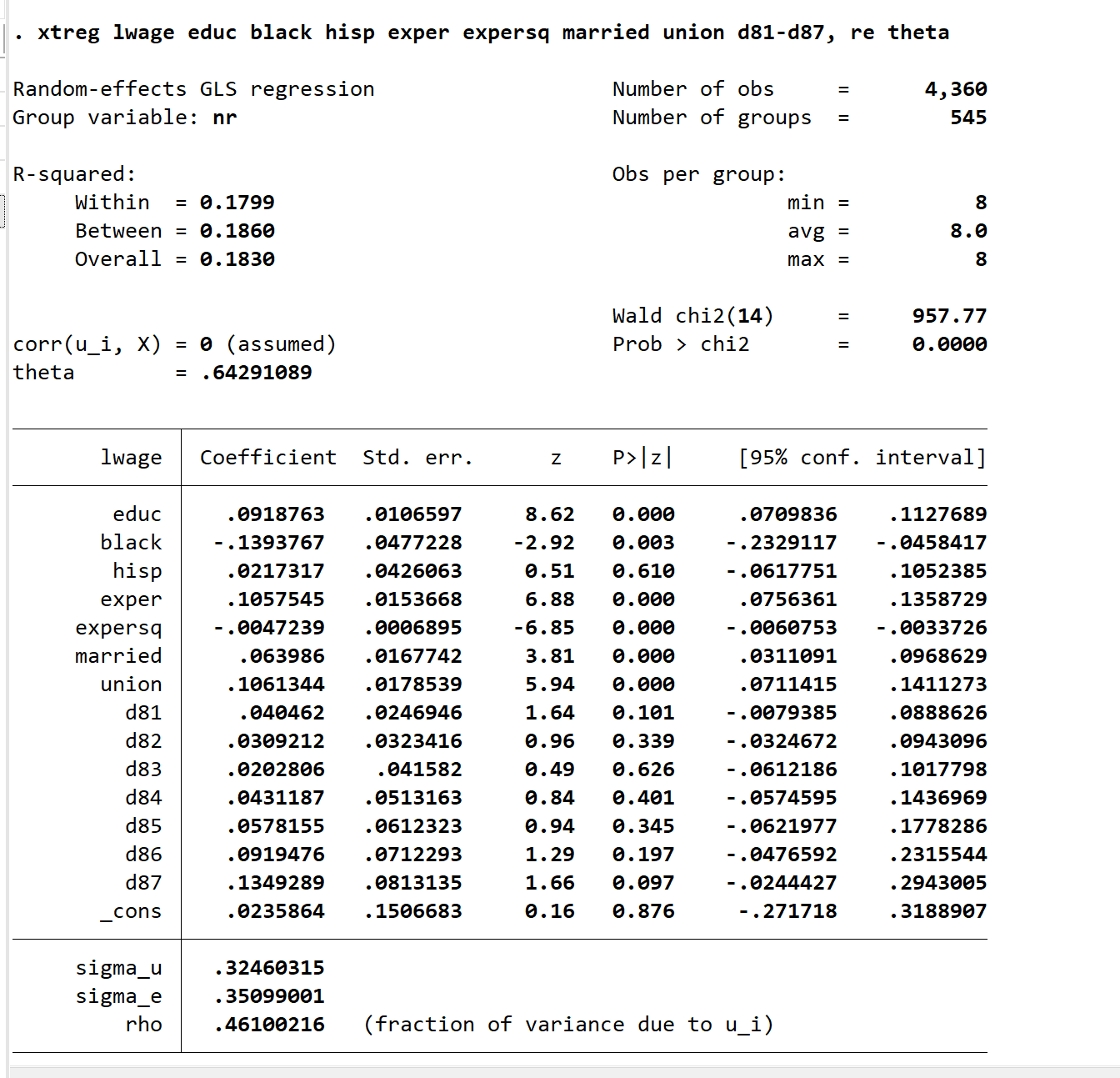
xtreg lwage educ black hisp exper expersq married union d81-d87, re theta

这个theta就是\(\lambda\)

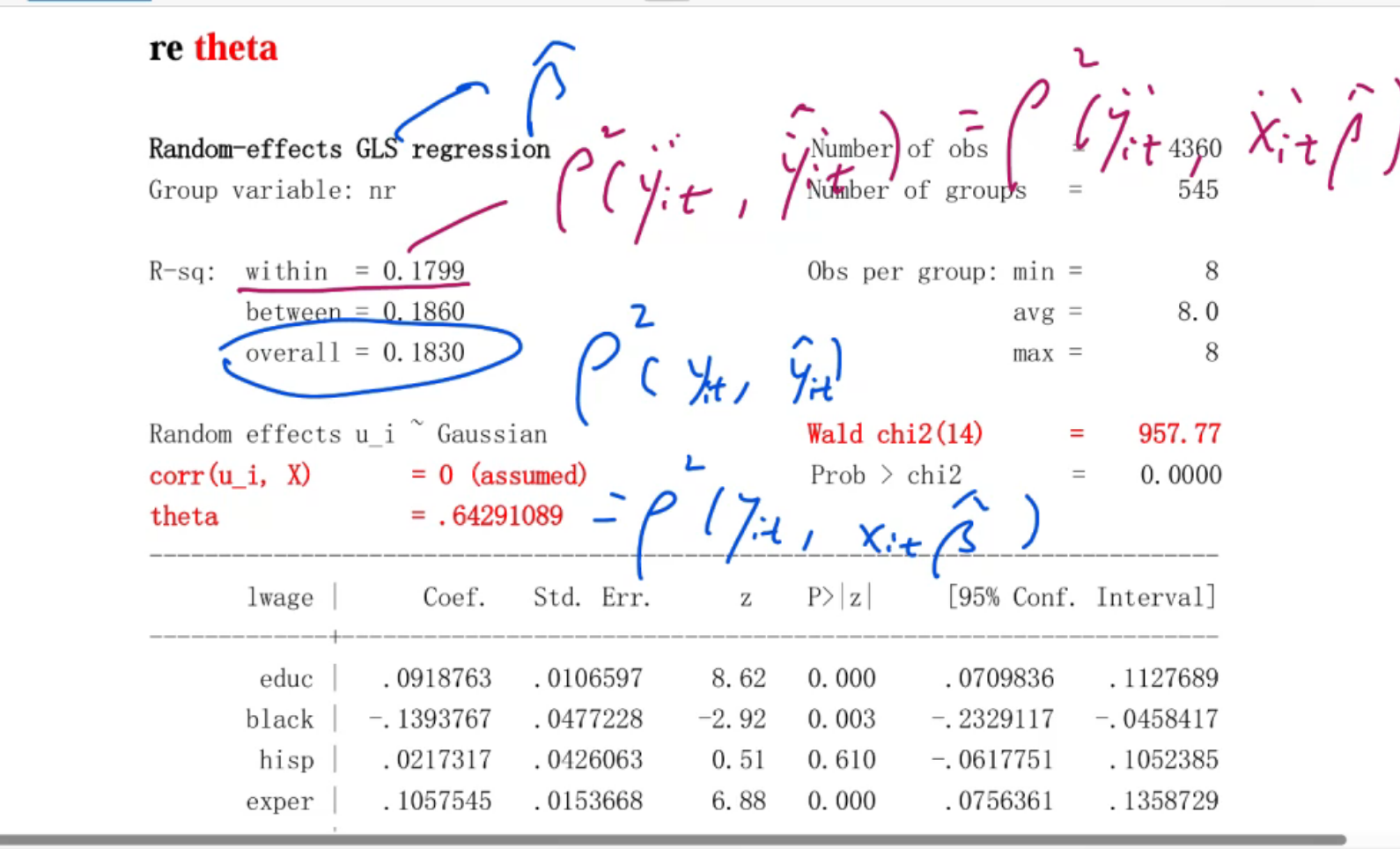
各种R^2怎么来的？

wald统计量与F统计量的关系，自由度
这个wald统计量说明这14个x作为整体是对Y有影响的，是显著的。

theta就是\(\lambda\),是用来估计的。如果考试考到它，会给公式
这里MAX=8,表示T=8

\[\hat{\lambda} = 1 - \left( \frac{1}{1 + T \left( \frac{\hat{\sigma}_a^2}{\hat{\sigma}_u^2} \right)} \right)^{1/2} \]

ols,fe,re这些模型之间的选择

ols,fe

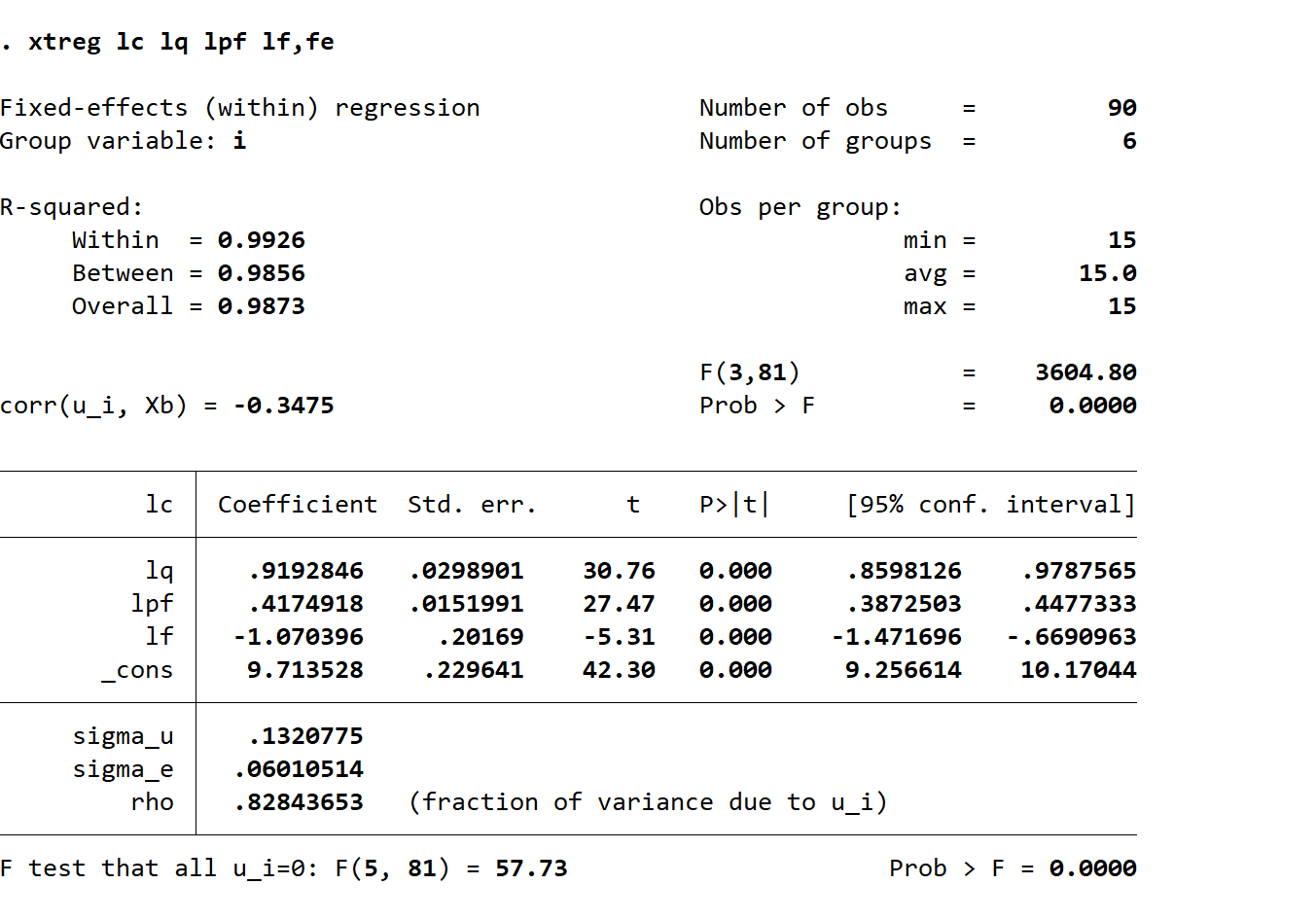
最下面的F检验决定，如果拒绝原假设，应该用FE

ols,re

拉格朗日乘数检验Lagrange multiplier test

原假设是a的方差=0，也就是\(v_{it},v_{is}\)协方差为0，即不相关。即原假设方法为混合ols,如果拒绝原假设用re

检验两计算：1、依据公式慢慢算

xtreg lc lq lpf lf,re
xttest0

这里是'0'不是'o'

fe,re

Hausman检验
这是一个方法，在工具变量哪里讲过。

这个表格很重要

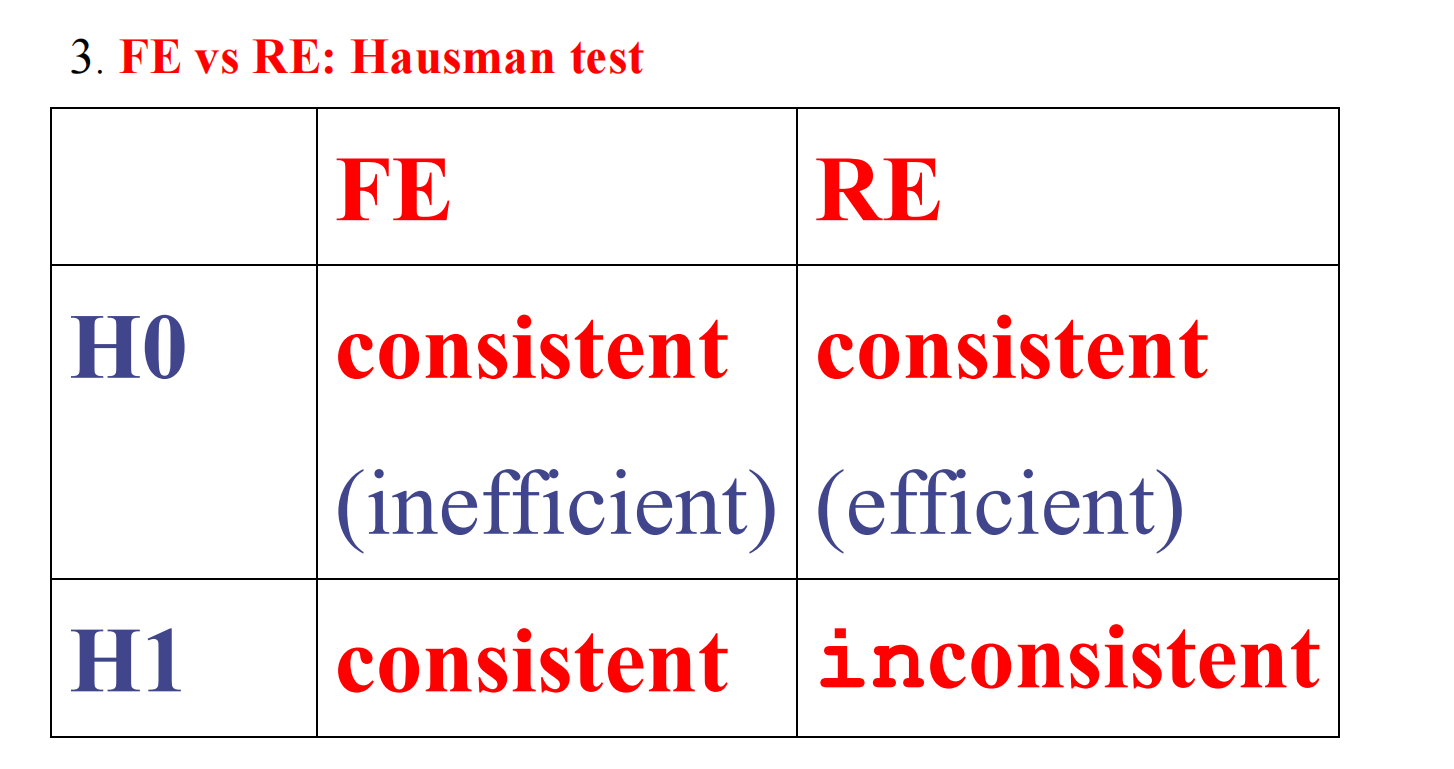
原假设协方差=0，即RE
在对立假设下面RE为什么是不一致的？一直不一致关键看模型误差项与解释变量相关不相关。
构造统计量：