多元统计分析讨论四
多元统计分析讨论四
一、问题
UC Berkeley在研究生录取时是否存在性别差异?
以下表格展示了1973年UC Berkeley六个主要研究生项目中男性和女性的申请人数及录取人数,请分析当时是否存在性别差异?
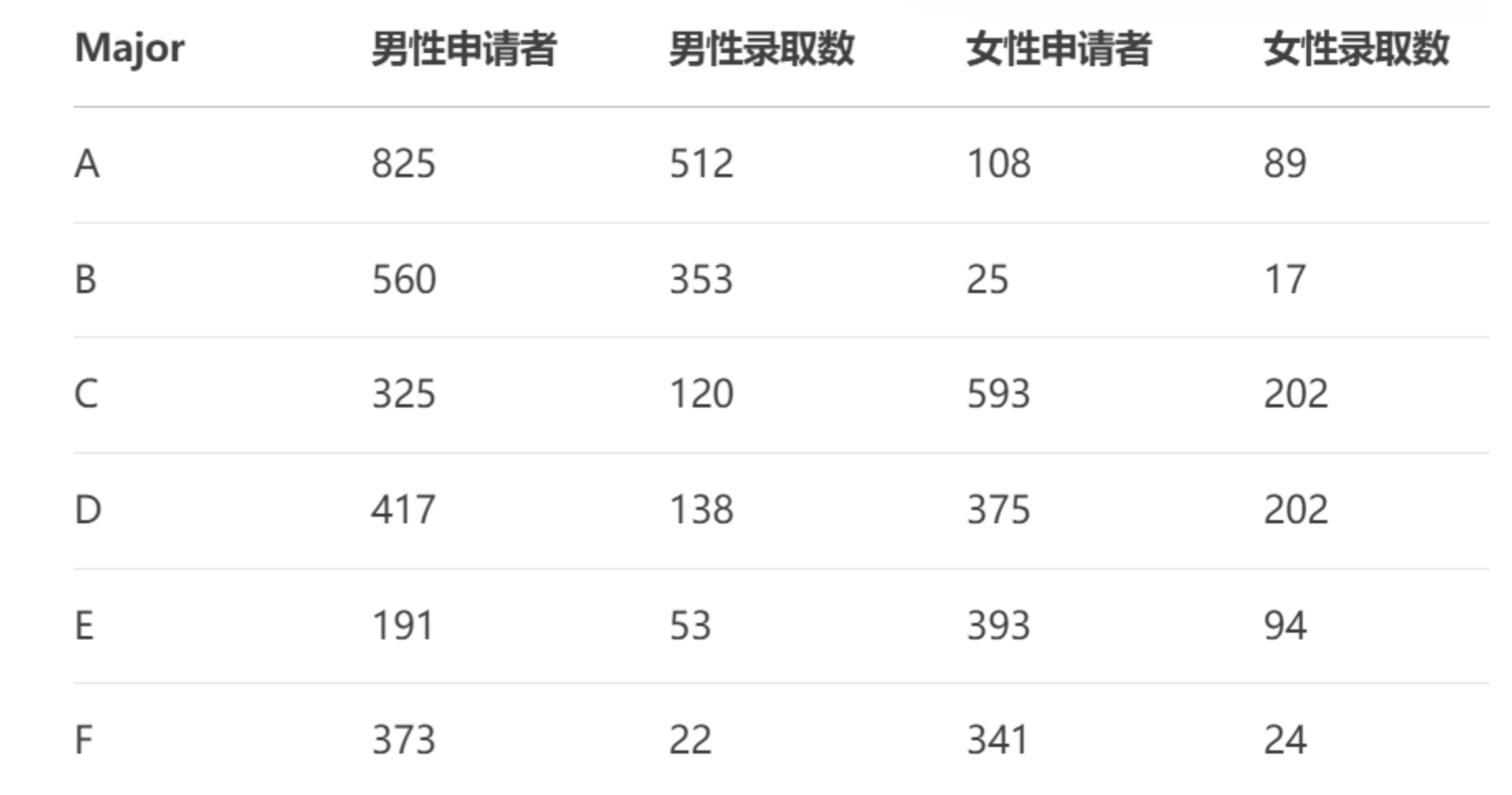
二、代码分析
2.1 总体情况(不分专业)
data <- data.frame(
Major = c("A", "B", "C", "D", "E", "F"),
MaleApplicants = c(825, 560, 325, 417, 191, 373),
MaleAdmits = c(512, 353, 120, 138, 53, 22),
FemaleApplicants = c(108, 25, 593, 375, 393, 341),
FemaleAdmits = c(89, 17, 202, 202, 94, 24)
)
# --------------------------总体(部分专业)---------------------
## 构建总表
total_male_applicants <- sum(data$MaleApplicants)
total_male_admits <- sum(data$MaleAdmits)
total_female_applicants <- sum(data$FemaleApplicants)
total_female_admits <- sum(data$FemaleAdmits)
overall_table <- matrix(c(
total_male_admits, total_male_applicants - total_male_admits,
total_female_admits, total_female_applicants - total_female_admits
), nrow = 2, byrow = TRUE)
colnames(overall_table) <- c("Admitted", "Rejected")
rownames(overall_table) <- c("Male", "Female")
# 卡方检验
chisq.test(overall_table)
# fisher 检验
fisher.test(overall_table)
2.1.1 结果分析
| 检验方法 | p 值 | 显著性 | odds ratio | 95% 置信区间 | 结论 |
|---|---|---|---|---|---|
| 卡方检验 | 5.17e-12 | ✅ 显著 | - | - | 存在总体性别差异 |
| Fisher 精确检验 | 3.70e-12 | ✅ 显著 | 1.54 | [1.36, 1.75] | 男性的录取优势明显高于女性 |
2.1.2 图示
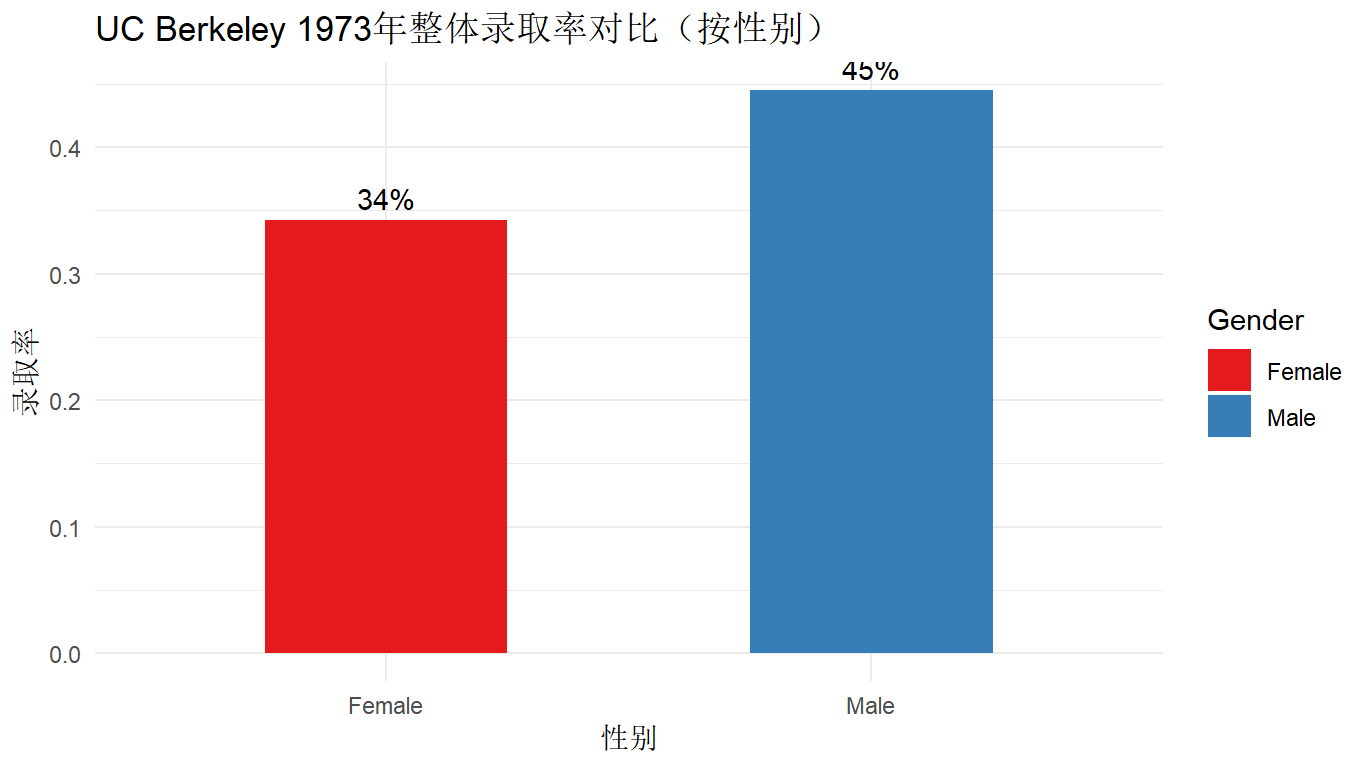
2.2 分专业情况
# -----------------分专业分析---------------------------
for (i in 1:nrow(data)) {
cat("\n--- 专业", data$Major[i], "---\n")
admits <- c(data$MaleAdmits[i], data$MaleApplicants[i] - data$MaleAdmits[i],
data$FemaleAdmits[i], data$FemaleApplicants[i] - data$FemaleAdmits[i])
major_table <- matrix(admits, nrow = 2, byrow = TRUE)
colnames(major_table) <- c("Admitted", "Rejected")
rownames(major_table) <- c("Male", "Female")
print(major_table)
cat("卡方检验:\n")
print(chisq.test(major_table, simulate.p.value = TRUE)) # 避免样本太小
cat("Fisher精确检验:\n")
print(fisher.test(major_table))
}
2.2.1 结果分析
| 专业 | 卡方 p值 | Fisher p值 | 显著性判断 (p < 0.05) | 倾向性别(Fisher OR) | 解读 |
|---|---|---|---|---|---|
| A | 0.0005 | 1.67e-05 | ✅ 显著 | 男性录取比例更高 (OR = 0.35) | 存在性别差异,男性录取机会明显低于女性 |
| B | 0.6682 | 0.6771 | ❌ 不显著 | 无明显性别倾向 | 无差异 |
| C | 0.3758 | 0.3866 | ❌ 不显著 | 略倾向女性 (OR = 1.13) | 差异不显著 |
| D | 0.0005 | 5.05e-09 | ✅ 显著 | 女性录取比例更高 (OR = 0.42) | 存在性别差异,男性录取机会明显低于女性 |
| E | 0.3458 | 0.3604 | ❌ 不显著 | 略倾向女性 (OR = 1.22) | 差异不显著 |
| F | 0.5482 | 0.5458 | ❌ 不显著 | 无明显性别倾向 | 无差异 |
2.2.2 图示
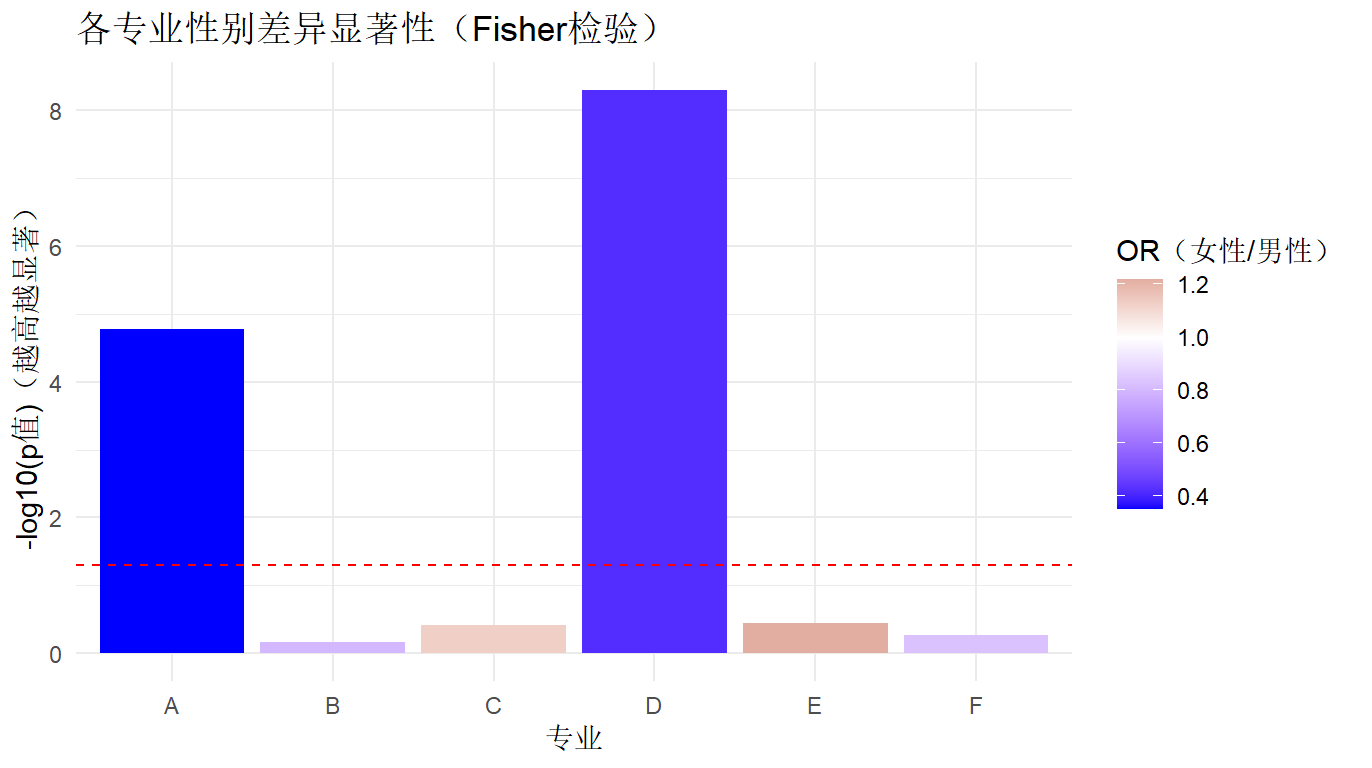
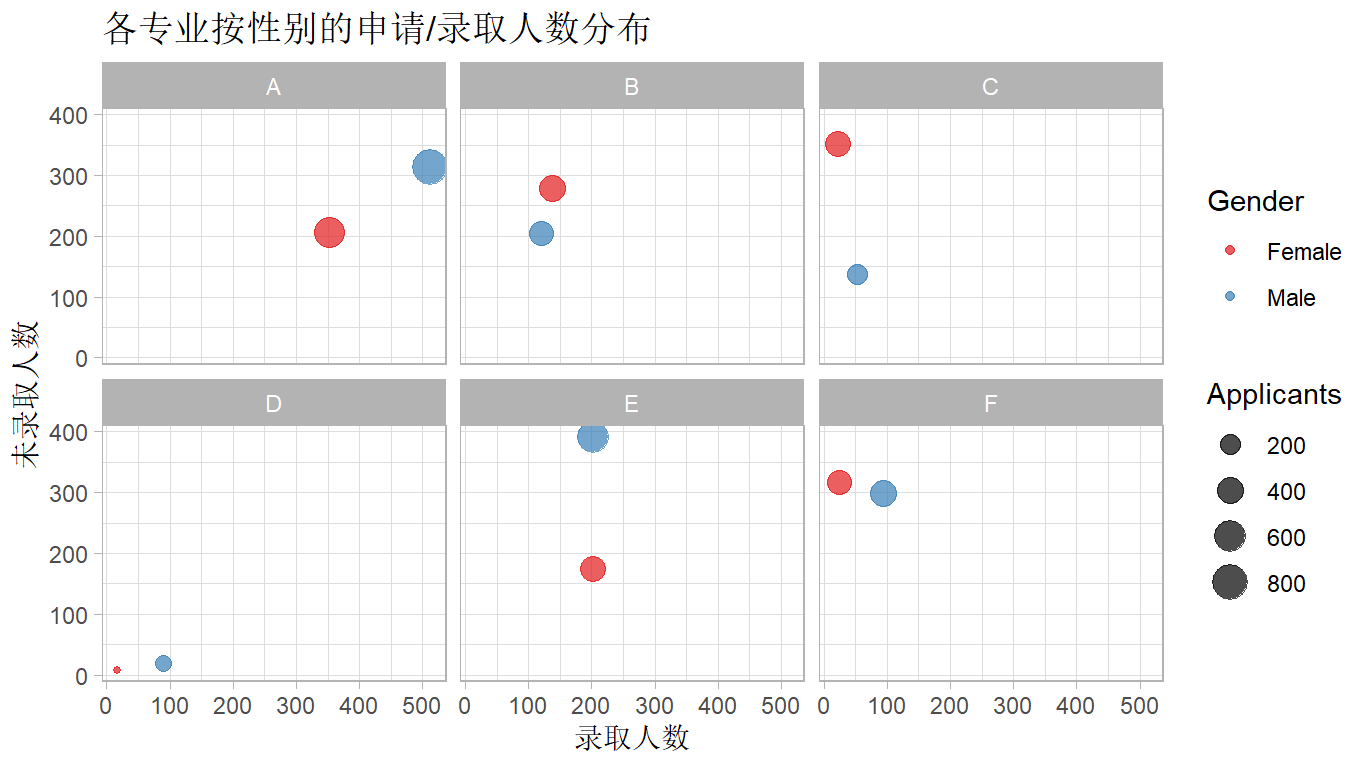
三、结论
从总体看,是存在显著的性别差异。但在分专业分析中,只有A和D两个专业的卡方检验和Fisher精确检验都显示出了显著的性别差异,而其余专业则没有显著的性别差异,或者说是在统计意义上不显著。那基于此,我们在考虑研究生录取的性别差异时,需要具体分析各个专业的具体情况。否则,可能造成辛普森悖论。
四、附录
4.1 检验方式适用情况
- 卡方检验:k-ways
- Fisher精确检验:two-ways
4.2 OR解释规则
OR 解释规则(通用)[男性处于分子]:
OR = 1:男女录取机会相等
OR < 1:男性录取机会 低于 女性
OR > 1:男性录取机会 高于 女性
4.3 代码
# --------------------------------------------------------------------------
data <- data.frame(
Major = c("A", "B", "C", "D", "E", "F"),
MaleApplicants = c(825, 560, 325, 417, 191, 373),
MaleAdmits = c(512, 353, 120, 138, 53, 22),
FemaleApplicants = c(108, 25, 593, 375, 393, 341),
FemaleAdmits = c(89, 17, 202, 202, 94, 24)
)
# --------------------------总体(部分专业)---------------------
## 构建总表
total_male_applicants <- sum(data$MaleApplicants)
total_male_admits <- sum(data$MaleAdmits)
total_female_applicants <- sum(data$FemaleApplicants)
total_female_admits <- sum(data$FemaleAdmits)
overall_table <- matrix(c(
total_male_admits, total_male_applicants - total_male_admits,
total_female_admits, total_female_applicants - total_female_admits
), nrow = 2, byrow = TRUE)
colnames(overall_table) <- c("Admitted", "Rejected")
rownames(overall_table) <- c("Male", "Female")
# 卡方检验
chisq.test(overall_table)
# fisher 检验
fisher.test(overall_table)
# -----------------分专业分析---------------------------
for (i in 1:nrow(data)) {
cat("\n--- 专业", data$Major[i], "---\n")
admits <- c(data$MaleAdmits[i], data$MaleApplicants[i] - data$MaleAdmits[i],
data$FemaleAdmits[i], data$FemaleApplicants[i] - data$FemaleAdmits[i])
major_table <- matrix(admits, nrow = 2, byrow = TRUE)
colnames(major_table) <- c("Admitted", "Rejected")
rownames(major_table) <- c("Male", "Female")
print(major_table)
cat("卡方检验:\n")
print(chisq.test(major_table, simulate.p.value = TRUE)) # 避免样本太小
cat("Fisher精确检验:\n")
print(fisher.test(major_table))
}
# 各专业按性别的录取率条形图
library(ggplot2)
library(dplyr)
# 构建长格式数据
data_long <- data.frame(
Major = rep(data$Major, each = 2),
Gender = rep(c("Male", "Female"), times = nrow(data)),
Applicants = c(data$MaleApplicants, data$FemaleApplicants),
Admits = c(data$MaleAdmits, data$FemaleAdmits)
)
data_long <- data_long %>%
mutate(AdmitRate = Admits / Applicants)
# 绘制条形图
ggplot(data_long, aes(x = Major, y = AdmitRate, fill = Gender)) +
geom_bar(stat = "identity", position = "dodge") +
labs(
title = "各专业中按性别的录取率",
x = "专业",
y = "录取率"
) +
theme_minimal() +
scale_fill_brewer(palette = "Set1")
# 每个专业的录取人数与申请人数气泡图(比例视角)
data_long <- data_long %>%
mutate(Rejection = Applicants - Admits)
ggplot(data_long, aes(x = Admits, y = Rejection, color = Gender, size = Applicants)) +
geom_point(alpha = 0.7) +
facet_wrap(~ Major) +
labs(
title = "各专业按性别的申请/录取人数分布",
x = "录取人数",
y = "未录取人数"
) +
theme_light() +
scale_color_brewer(palette = "Set1")
# 热图:各专业的 Fisher 检验 p 值热图 + odds ratio
library(ggplot2)
library(tibble)
# 汇总统计结果
summary_df <- tribble(
~Major, ~FisherP, ~OR,
"A", 1.67e-05, 0.35,
"B", 0.6771, 0.80,
"C", 0.3866, 1.13,
"D", 5.05e-09, 0.42,
"E", 0.3604, 1.22,
"F", 0.5458, 0.83
)
# 绘图
ggplot(summary_df, aes(x = Major, y = -log10(FisherP), fill = OR)) +
geom_bar(stat = "identity") +
geom_hline(yintercept = -log10(0.05), linetype = "dashed", color = "red") +
scale_fill_gradient2(low = "blue", mid = "white", high = "darkred", midpoint = 1) +
labs(
title = "各专业性别差异显著性(Fisher检验)",
x = "专业",
y = "-log10(p值)(越高越显著)",
fill = "OR(女性/男性)"
) +
theme_minimal()
# 总体录取率按性别条形图
overall_df <- data.frame(
Gender = c("Male", "Female"),
Admits = c(sum(data$MaleAdmits), sum(data$FemaleAdmits)),
Applicants = c(sum(data$MaleApplicants), sum(data$FemaleApplicants))
)
overall_df$Rejects <- overall_df$Applicants - overall_df$Admits
overall_df$Rate <- overall_df$Admits / overall_df$Applicants
library(ggplot2)
ggplot(overall_df, aes(x = Gender, y = Rate, fill = Gender)) +
geom_bar(stat = "identity", width = 0.5) +
labs(
title = "UC Berkeley 1973年整体录取率对比(按性别)",
y = "录取率", x = "性别"
) +
theme_minimal() +
scale_fill_brewer(palette = "Set1") +
geom_text(aes(label = scales::percent(Rate)), vjust = -0.5)
# 分专业录取率对比 + 总体线标识
# 使用 data_long 数据
ggplot(data_long, aes(x = Major, y = AdmitRate, fill = Gender)) +
geom_bar(stat = "identity", position = "dodge") +
geom_hline(yintercept = overall_df$Rate[1], linetype = "dashed", color = "#1f78b4", size = 0.5) +
geom_hline(yintercept = overall_df$Rate[2], linetype = "dashed", color = "#e31a1c", size = 0.5) +
labs(
title = "各专业性别录取率对比(含总体录取率)",
y = "录取率",
x = "专业"
) +
theme_minimal() +
scale_fill_brewer(palette = "Set1")
# 整体显著但分专业不显著”的辛普森悖论现象
library(dplyr)
library(tidyr)
# 每专业录取率差异(男 - 女)
delta_rate <- data_long %>%
select(Major, Gender, AdmitRate) %>%
pivot_wider(names_from = Gender, values_from = AdmitRate) %>%
mutate(Diff = Male - Female)
ggplot(delta_rate, aes(x = Major, y = Diff)) +
geom_bar(stat = "identity", fill = "steelblue") +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(title = "各专业男性与女性录取率差(男 - 女)", y = "录取率差", x = "专业") +
theme_minimal()
本文来自博客园,作者:xia0ya,转载请注明原文链接:https://www.cnblogs.com/xia0ya/p/18871569


 浙公网安备 33010602011771号
浙公网安备 33010602011771号